917

4.31.

2; 3;

5 ,

6; 1; 4 ,

.

4.32.

8;

3;

7 ,

2; 4; 0 ,

.

4.33.

7; 2;

4

,

5;

1; 3 ,

.

4.34.

3;

1;

2

,

4;

7; 6

,

4 .

4.35.

2; 6; 3

,

4; 8;

4 ,

.

4.36.

1;

5; 2

,

3;

4; 6

,

.

Третий уровень сложности

Задание 5. Даны вершины треугольника

, ,

. Определить длину

биссектрисы его внутреннего угла при вершине .

5.1.

2;

1; 2 ,

8; 1;

1 ,

20; 5;

4 .

5.2.

5; 8;

2 ,

1; 6;

5 ,

13; 2; 2 .

5.3.

9;

4; 5 ,

3;

2; 2 ,

9; 2;

1 .

5.4.

11; 8;

1 ,

5; 6;

4 ,

7; 2;

1 .

5.5.

8; 5; 4 ,

2; 3; 1 ,

10; 7; 4 .

5.6.

1;

5;

8 ,

7;

3;

5 ,

11; 0; 7 .

5.7.

2;

10; 1 ,

4;

8;

2 ,

16;

5;

6 .

5.8.

7; 4;

5 ,

1; 2;

2 ,

11; 6; 1 .

5.9.

2;

5;

7 ,

4;

3;

4 ,

8; 1;

1 .

5.10.

4;

8; 1 ,

2;

6;

2 ,

14;

2; 1 .

5.11.

5;

9;

4 ,

1;

7;

1 ,

13;

3; 2 .

5.12.

1;

8; 5 ,

5;

6; 2 ,

17;

2;

1 .

5.13.

15;

7; 6 ,

9;

5; 3 ,

3;

1; 0 .

5.14.

8; 1;

4 ,

2;

1;

1 ,

10;

5; 2 .

5.15.

14;

3; 1 ,

2;

7;

2 ,

4;

5; 1 .

5.16.

10;

3; 2 ,

4;

1;

1 ,

8; 3;

4 .

5.17.

9; 6; 7 ,

3; 4; 4 ,

9; 0; 1 .

5.18.

7;

3; 8 ,

5; 1; 5 ,

11;

2; 3 .

5.19.

3;

7; 1 ,

9;

3;

2 ,

15;

1;

5 .

5.20.

11; 4;

2 ,

1; 8; 1 ,

7; 6; 4 .

5.21.

8;

1;

4 ,

2; 1;

1 ,

14; 5; 2 .

5.22.

14; 3;

5 ,

8; 1;

2 ,

4; 5; 1 .

5.23.

10; 3;

2 ,

4; 1; 1 ,

8; 5; 4 .

5.24.

9;

5;

4 ,

3;

3;

1 ,

9; 1; 2 .

5.25.

5;

4; 5 ,

1;

2; 2 ,

13; 1; 6 .

5.26.

0;

9;

5 ,

6;

7;

2 ,

18;

3; 1 .

5.27.

8; 0;

4 ,

2;

2;

1 ,

10;

6; 2 .

5.28.

4; 5; 9 ,

2; 3; 6 ,

14;

1; 3 .

5.29.

7;

5; 10 ,

1;

3; 7 ,

11; 1; 4 .

5.30.

10;

7;

4 ,

4;

5;

1 ,

8;

1; 2 .

5.31.

8;

7;

2 ,

2;

5;

5 ,

10;

1;

8 .

5.32.

11; 4;

7 ,

5; 2;

4 ,

7;

2;

1 .

30

5.33.

4; 1;

1 ,

2;

1;

4 ,

14; 3;

7 .

5.34.

13;

3; 5 ,

7;

1; 2 ,

5;

5;

1 .

5.35.

7;

5; 4 ,

1;

3; 1 ,

11; 0;

3 .

5.36.

5; 9; 4 ,

1; 7; 1 ,

13; 4;

3 .

Тесты

Вариант 1

Первый уровень сложности.

1. Координаты точки, симметричной точке

3; 2;

1

относительно

плоскости

, равны:

1)

3;

2;

1

2)

3; 2;

1

3)

3; 2; 1

4)

3; 2; 1

5)

3;

2;

1

2. Расстояние между точками

1; 5;

6

и

3; 4;

7

равно:

1)

√14

2) 14

3)

3√2

4) 18

5)

3√2

3. Даны точки

3;

8;

9

и

5; 0;

4 . Координаты середины от-

резка

равны:

1)

2;

2;

2)

8; 8; 13

3)

8;

8;

13

4)

4; 4;

5)

4;

4;

Второй уровень сложности.

4. Расстояние от начала координат до точки

4; 12; 6

равно:

1)

196

2) 14

3)

49

4) 7

5)

14

5. Точка

делит отрезок между точками

2;4; 7

и

3;

5;

8

в отношении

3. Координаты точки

равны:

1)

;

;

2)

;

;

3)

7; 11;

17

4)

;

;

5)

;

;

Третий уровень сложности.

6. Координаты точки, расположенной на оси

и равноудал нной от

точек

2; 4; 1

и

3; 2; 5 , равны:

1)

0; 0;

2)

0;

; 0

3)

; 0; 0

4)

0; 0;

5)

0;

; 0

Вариант 2

Первый уровень сложности.

1. Координаты точки, симметричной точке

6; 8; 1

относительно

оси абсцисс, равны:

1)

6;

8;

1

2)

6; 8;

1

3)

6; 8; 1

4)

6; 8;

1

5)

6; 8;

1

2. Расстояние между точками

4;

3; 8

и

5; 0; 7 равно:

1)

√91

2) √91

3)

91

4) √71

5) 71

3. Даны точки

8; 6; 1

и

3; 4;

3 . Координаты середины от-

резка

равны:

31

1)

; 5;

1

2)

;

5; 1

3)

5; 10;

2

4)

5;

10; 2

5)

;

;

Второй уровень сложности.

4. Расстояние от начала координат до точки

4; 2;

4

равно:

1) 6

2) 36

3) 2

4) 4

5)

6

5. Точка

делит отрезок между точками

4; 3; 9

и

8;

5; 1

в отношении

. Координаты точки

равны:

1)

28; 1; 5

2)

28; 1; 5

3)

;

; 5

4)

;

; 5

5)

;

;

Третий уровень сложности.

6. Координаты точки, расположенной в плоскости

и равноудал н-

ной от точек

1;

1; 5 ,

3; 4; 4

и

4; 6; 1 , равны:

1)

5; 16; 0

2)

0;

5; 16

3)

0; 16;

5

4)

16;

5; 0

5)

16; 0;

5

положное направление.

Длиной или модулем вектора

называется число, равное длине от-

резка

. Используется обозначение: |

|

пользуется обозначение:

̅. Нулевой вектор не имеет определ нного направ-

ления и имеет длину, равную нулю.

Вектор, противоположный вектору

, обозначается ; вектор, про-

тивоположный вектору

, обозначается .

Три вектора называются компланарными, если они лежат в одной

плоскости или в параллельных плоскостях.

Пример 2.1. В прямоугольнике

показаны векторы (рис. 2.2).

лельны, выпишем пары коллинеарных векторы:

и ,

и .

33

Рис. 2.2. Прямоугольник

(к Примеру 2.1)

2) Выпишем сонаправленные векторы. Для этого среди коллинеарных

векторов выберем векторы, имеющие одинаковые направления:

и .

равных векторов совпадают с парами сонаправленных векторов:

и .

Ответ: 1)

и ,

и ; 2)

и ; 3)

и ; 4)

и .

1. Сложение. Пусть даны два вектора и . Суммой

называется

вектор, который ид т из начала вектора

в конец вектора ,

при условии,

что вектор приложен к концу вектора

. Покажем на рисунке

(рис. 2.3):

Рис. 2.3. Сложение векторов по правилу треугольника

Сложение векторов, выполненное указанным образом, называют пра-

вилом треугольника.

Замечание. Если конец вектора

совпадает с началом вектора , то

сумма

является нулевым вектором:

̅.

2. Умножение вектора на число. Пусть даны вектор

и число . Про-

изведением

называется вектор, коллинеарный вектору

, имеющий длину

| | ∙ |

| и направление такое же, как у вектора , если

0, и противопо-

ложное, если

0.

Замечание 1. Если

̅или

0, то произведение имеет модуль,

1.

. Переместительное свойство.

Это свойство говорит о том, что сумма любых двух векторов не зави-

сит от порядка слагаемых.

Доказательство. Приложим векторы

и к одной точке и по-

строим на этих векторах параллелограмм

таким образом, что

равны, то

,

.

В ∆

по правилу треугольника

. В ∆

по

правилу треугольника

. Таким образом,

.

Замечание. Если на векторах

и , привед нных к общему началу, по-

строить параллелограмм, то

является диагональю этого параллело-

грамма, идущей из общего начала

и . Такое правило сложения векторов

называется правилом параллелограмма.

2.

̅

̅. Сочетательное свойство.

Доказательство. Расположим векторы ,

и ̅так, чтобы вектор

был приложен к концу вектора

,

а вектор ̅приложен к концу вектора .

Построим на этих векторах четыр хугольник

так, что

,

В ∆

по правилу треугольника

. В ∆

по

правилу треугольника

̅.

В ∆

по правилу треугольника

̅. В ∆

по

правилу треугольника

̅.

35

Таким образом,

̅

̅.

Замечание 1. Аналогично можно получить общее правило сложения

векторов. Для того чтобы построить сумму n векторов ,

, … ,

нужно к

концу вектора

приложить вектор

, затем к концу вектора

приложить

вектор

, затем к концу вектора

приложить вектор

и т. д., затем к

концу вектора

приложить вектор

. Тогда суммой

…

будет вектор, идущий из начала вектора

в конец

вектора

(рис. 2.6).

своих слагаемых.

3.

, где , . Распределительное свойство.

Это свойство означает, что при растяжении вектора в

раз по-

лучается такой же вектор, как при сложении вектора , растянутого в

раз,

с вектором

, растянутым в

раз.

4.

, где

,

. Сочетательное свойство.

Это свойство означает,

что при растяжении вектора в раз и затем

ещ

в

раз получается такой же вектор, как при растяжении вектора

сразу

в

раз.

5.

,

. Распределительное свойство.

Доказательство. Это тождество следует из теории подобия фигур.

Вектор

является диагональю параллелограмма, построенного на век-

торах

и

, в предположении, что и приведены к общему началу. При

растяжении векторов , и

в раз этот параллелограмм изменяется

Рис. 2.7. Распределительное свойство

Таким образом,

является диагональю параллелограмма, по-

строенного на векторах

и . Отсюда

.

Указанные свойства линейных операций дают право выполнять пре-

образования в векторной алгебре так же, как в обычной алгебре.

2.3. Вычитание векторов в векторной форме

Пусть даны два произвольных вектора

и . Разностью

назы-

вается вектор, который в сумме с вектором

составляет вектор

(рис. 2.8).

Операцию вычитания из вектора

вектора

можно заменить сложе-

нием вектора

с вектором, противоположным вектору

:

.

Пример 2.2. Раскрыть скобки и упростить выражение: 4 3

5

2 .

Решение. Используя свойства линейных операций, получаем:

4 3

5

2

4 3

4 5

2

12

20

2

12

2

20

12

2

20

14

20 .

Ответ: 14

20 .

Пример 2.3. Даны векторы и . Построить следующие векторы:

1) 2 ; 2) ; 3)

2 ; 4)

; 5)

; 6) 2

.

Решение.

1) Вектор 2

получается из вектора

растяжением его в 2 раза

(рис. 2.9).

2) Вектор

получается из вектора

изменением его направления на

Рис. 2.9. Построение векторов (к Примеру 2.3)

3) Вектор

2 получается из вектора 2

изменением его направления

на противоположное (рис. 2.9).

4) Вектор

получается из вектора сжатием его в 2 раза (рис. 2.9).

5) Вектор

получается из вектора

изменением его направления

на противоположное (рис. 2.9).

6) Вектор 2

получается сложением векторов 2 и

по правилу

параллелограмма (рис. 2.9).

Пример 2.4. В треугольнике

вектор

и вектор

.

Построить каждый из следующих векторов: 1)

; 2)

; 3)

;

4)

.

Решение.

1) Достроим треугольник

до параллелограмма

. Обозначим

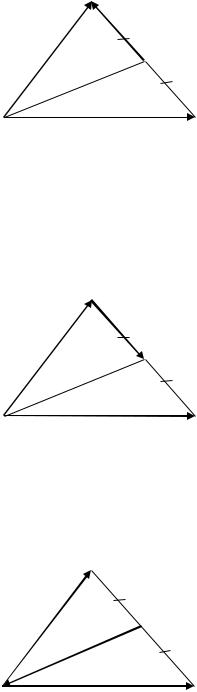
получаем, что

. Таким образом, вектор

совпадает с ме-

дианой треугольника, выходящей из той же точки, что и векторы

и .

2) Обозначим через

середину стороны

. Тогда

. По

правилу вычитания векторов

. Тогда вектор

(рис. 2.11).

Рис. 2.11. Построение вектора

(к Примеру 2.4 (2))

3) Искомый вектор можно представить следующим образом:

, то есть искомый вектор противоположен вектору

, следова-

тельно, совпадает с вектором

, где

– середина стороны

(рис. 2.12).

Рис. 2.12. Построение вектора

(к Примеру 2.4 (3))

4) Искомый вектор противоположен вектору

, следовательно, сов-

падает с вектором

, где – середина стороны

(рис. 2.13).

Рис. 2.13. Построение вектора

(к Примеру 2.4 (4))