917

Пример 2.5. В параллелепипеде

заданы векторы, сов-

падающие с его р брами:

,

,

̅. Построить каждый из

следующих векторов: 1)

̅; 2)

̅; 3)

̅; 4)

̅; 5)

̅.

Решение.

1) По правилу параллелограмма

. Затем так же

по правилу параллелограмма

̅, то есть искомый

вектор совпадает с вектором

. Иначе, искомый вектор совпадает с диаго-

Рис. 2.14. Построение вектора

̅(к Примеру 2.5 (1))

2) По правилу параллелограмма

. Обозначим

через середину ребра

. Тогда

̅. Обозначим через се-

редину ребра

. Тогда по правилу параллелограмма

̅, то есть искомый вектор совпадает с вектором

(рис. 2.15).

Рис. 2.15. Построение вектора

̅(к Примеру 2.5 (2))

3) Обозначим через середину ребра

. Тогда

.

Обозначим через середину ребра

. Тогда

. Обозначим

через точку пересечения диагоналей параллелограмма

. По правилу

параллелограмма

. Обозначим через

точку пе-

ресечения диагоналей параллелограмма

. По правилу параллело-

грамма

̅, то есть искомый вектор совпадает

с вектором

(рис. 2.16).

Рис. 2.16. Построение вектора

̅(к Примеру 2.5 (3))

4) По правилу параллелограмма

. По правилу

вычитания векторов

̅, то есть искомый вектор

совпадает с вектором

(рис. 2.17).

Рис. 2.17. Построение вектора

̅(к Примеру 2.5 (4))

5) Так как по условию

, то

. Так как по усло-

вию

, то

. По правилу параллелограмма

. Обозначим через середину ребра

. Тогда

̅. По правилу треугольника

̅, то

есть искомый вектор совпадает с вектором

(рис. 2.18).

41

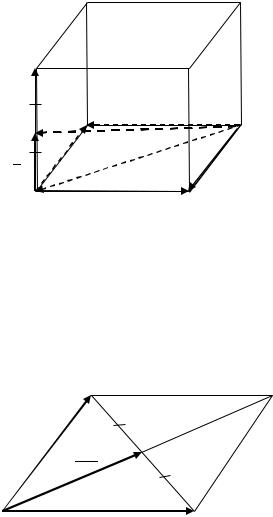
Рис. 2.18. Построение вектора

̅(к Примеру 2.5 (5))

Пример 2.6. В треугольнике

вектор

и вектор

. С

помощью векторов и выразить вектор

, совпадающий с медианой

.

Решение. Достроим треугольник

до параллелограмма

.

Точка – середина стороны

, а также точка пересечения диагоналей па-

раллелограмма (рис. 2.19).

чаем, что

.

Ответ:

.

̅, вектор

Пример 2.7. В треугольнике

вектор

, век-

тор

. С помощью векторов

,

, ̅выразить векторы, совпадающие с

медианами треугольника:

,

, .

Решение. Выполним черт ж (рис. 2.20).

Так как – середина стороны

, то

. Найд м иско-

мый вектор

из треугольника

по правилу треугольника:

̅

.

Так как – середина стороны

, то

. Найд м иско-

мый вектор

из треугольника

по правилу треугольника:

.

̅. Найд м иско-

Так как – середина стороны

, то

мый вектор

из треугольника

по правилу треугольника:

̅.

Ответ:

̅

,

,

̅.

Пример 2.8. В тетраэдре

даны р бра, выходящие из вершины

:

,

̅,

̅

. Выразить через эти векторы: 1) остальные р бра

тетраэдра; 2) медиану

грани

; 3) вектор

, где – центр тяжести

грани

.

Решение. Выполним черт ж (рис. 2.21).

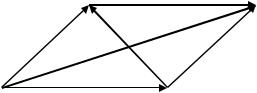
1) Из треугольника

по правилу вычитания векторов найд м век-

тор

, совпадающий с ребром

:

̅

. Из треугольника

по правилу вычитания векторов найд м вектор

, совпадающий с реб-

ром

:

̅

̅. Из треугольника

по правилу вычита-

ния векторов найд м вектор

, совпадающий с ребром

:

̅

.

2) Так как

– медиана, то – середина ребра

. Тогда из треуголь-

ника

можно выразить вектор

:

̅. Из

треугольника

по правилу вычитания векторов найд м вектор

, сов-

падающий с медианой

:

̅

̅ .

3) Так как – центр тяжести грани

, то

– точка пересечения

медиан грани

. Известно, что медианы треугольника в точке пересече-

ния делятся в отношении 2: 1,

считая от вершины. Поэтому точка

лежит

на медиане

и делит е

в отношении 2: 1, считая от точки

, то есть

̅

̅

̅

̅

по правилу

. Из треугольника

треугольника найд м вектор

:

̅

̅

̅

̅

.

̅

̅

̅,

̅

̅

Ответ: 1)

,

; 2)

̅

̅

; 3)

.

Пример

2.9. Даны | |

11,

23,

30. Определить

.

Решение. Привед м векторы

и к общему началу и построим на

той же точки, что и векторы

и , совпадает с вектором

, вторая диаго-

наль совпадает с вектором

(рис. 2.22).

Рис. 2.22. Векторы

и

(к Примеру 2.9)

2|

|

2

. Подставляем значения:

30

2 ∙ 11 2 ∙ 23 . Отсюда:

400,

20.

Ответ: 20.

Пример 2.10. Векторы

и

образуют угол

120 , прич м | | 3,

5. Определить

и

.

44

той же точки, что и векторы

и , совпадает с вектором

, вторая диаго-

наль совпадает с вектором

(рис. 2.23).

60

120

Рис. 2.23. Векторы

и

(к Примеру 2.10)

Воспользуемся теоремой косинусов. Получаем:

|

|

2 ∙ |

| ∙

∙ cos 60

3

5

2 ∙ 3 ∙ 5 ∙

19,

√19;

|

|

2 ∙ |

| ∙

∙ cos 120

3

5 2 ∙ 3 ∙ 5 ∙

∙

49,

7.

Ответ:

√19,

7.

2.4. Проекция вектора на ось

Пусть дана произвольная ось

и вектор

. Опустим из точек и

и . Получим вектор

(рис. 2.24).

l

Рис. 2.24. Проекция вектора на ось

Определение. Проекцией вектора

на ось l называется число, рав-

ное длине вектора

, взятой со знаком плюс, если направление вектора

совпадает с направлением оси и со знаком минус, если направление не

совпадает. Обозначение: пр

|

|.

l. Точку пересечения оси с отрезком

обозначим через С. Тогда

45

.

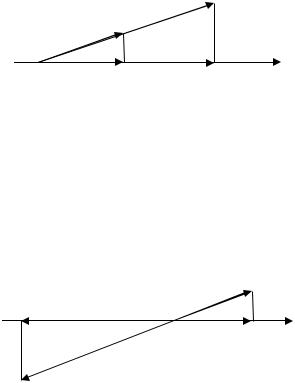
Запишем проекцию составленной суммы:

пр

пр

.

Найд м пр

. Для этого спроектируем векторы

,

,

,…,

на ось l. Получаем:

пр

пр

, пр

пр

, пр

пр

, …, пр

пр

.

Учитывая, что пр

, получаем:

пр

пр

пр

пр

пр

… пр .

Что и требовалось доказать.

3. При умножении вектора на число его проекция умножается на это

же число: пр

пр

. Обозначим

,

. Рассмотрим слу-

чай, когда

0 (рис. 2.27).

Из подобия треугольников

и

можно записать:

|

|

.

|

|

Так как |

|

пр

пр

, |

|

пр

пр , |

| |

|,

| | |

|, то:

пр

|

|

|

|| |

| |

. Отсюда пр

пр .

пр

|

|

|

|

Рассмотрим случай, когда

0 (рис. 2.28).

Из подобия треугольников

и

можно записать:

|

|

.

|

|

Так как |

|

пр

пр

, |

|

пр

пр

, | |

| |,

| | |

|, то:

пр

|

|

| ||

|

|

|

. Отсюда

пр

пр

пр

|

|

|

|

и пр

пр . Что и требовалось доказать.

47

Пример 2.11. Дан модуль вектора |

|

2 и углы

45 ,

60 ,

120 , образуемые вектором с осями

,

,

соответственно. Вычис-

лить проекции вектора

на эти оси.

Решение. Воспользуемся формулой нахождения проекции вектора на

ось через модуль вектора и угол его наклона к оси: пр

|

| ∙ cos .

Найд м проекцию вектора на ось

:

|

| ∙ cos

2 ∙ √

пр

2 ∙ cos 45

√2.

Найд м проекцию вектора на ось

:

пр

|

| ∙ cos

2 ∙ cos 60

2 ∙

1.

Найд м проекцию вектора на ось

:

пр

|

| ∙ cos

2 ∙ cos 120

2 ∙

1.

Ответ: пр

√2, пр

1, пр

1.

2.5. Проекции вектора на оси координат

Пусть в пространстве задана прямоугольная система координат. Рас-

смотрим произвольный вектор

. Пусть

– проекция вектора

на ось ;

– проекция вектора

на ось

;

– проекция вектора

на ось

. Про-

екции вектора

на оси координат называют его координатами и записывают:

;

;

.

2.6. Нахождение координат вектора

по известным координатам его начала и конца

Пусть даны две точки:

; ;

и

; ;

. Опустим из точек

и

перпендикуляры на ось

и обозначим их основания через

и .

Точки

и

имеют на оси Ox соответственно координаты

и

. Тогда

. Но

,

где

первая координата вектора

.

Следовательно,

.

Аналогично устанавливается, что

,

где

вторая координата вектора

и

, где

третья

координата вектора

.

Таким образом, координаты вектора

определяются по форму-

лам:

,

,

,

Пример 2.12. В пространстве даны точки

2; 3; 4 и

8; 3;

2 .

Найти координаты вектора .

Решение. По условию даны координаты начала и конца вектора

.

Для нахождения координат вектора

из координат конца вектора вычи-

таем координаты его начала. Получаем:

8

2; 3

3 ; 2 4

10; 6; 6 .

Ответ:

10; 6; 6 .

48