8.Контрольная работа

ВАРИАНТ 0

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

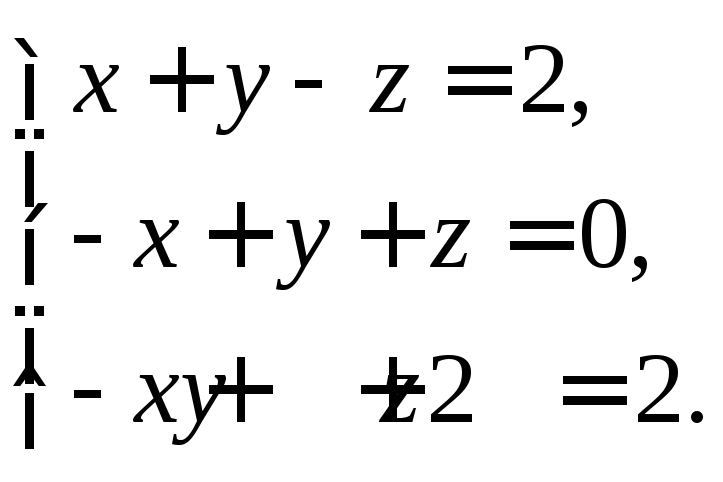
2. Найти множество решений системы линейных неравенств:

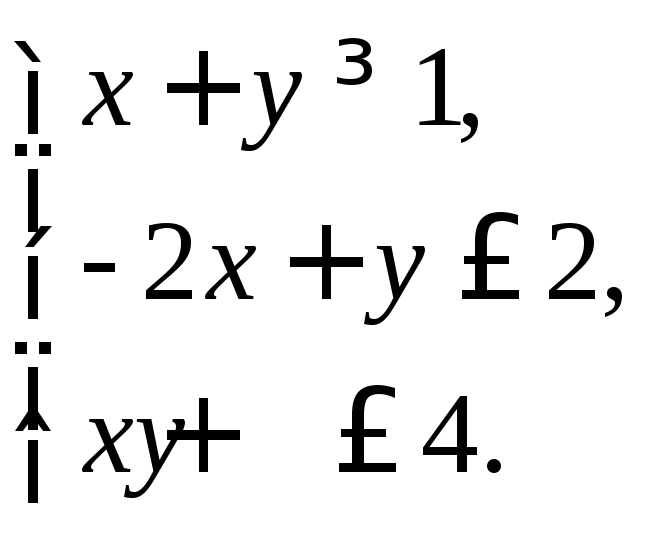
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 1

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

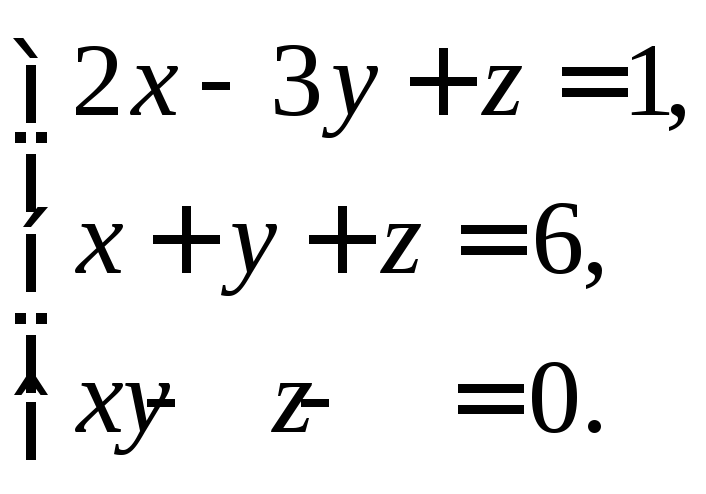
2. Найти множество решений системы линейных неравенств:

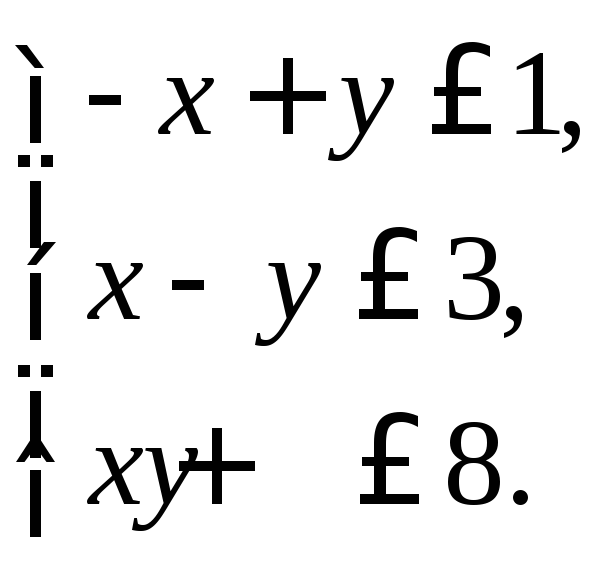
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 2

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

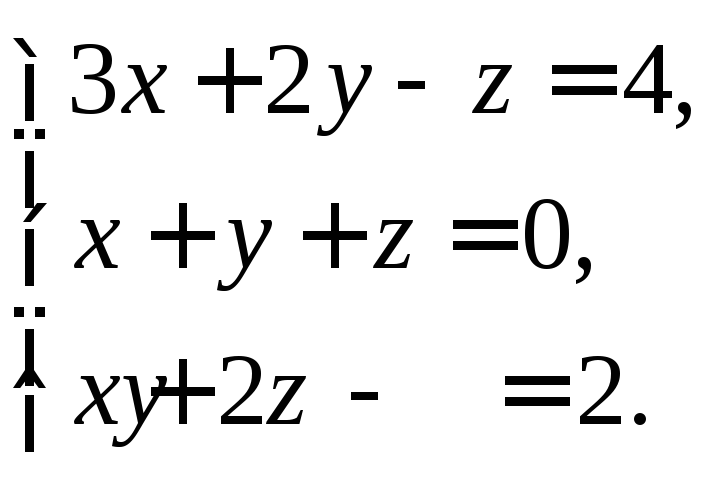
2. Найти множество решений системы линейных неравенств:

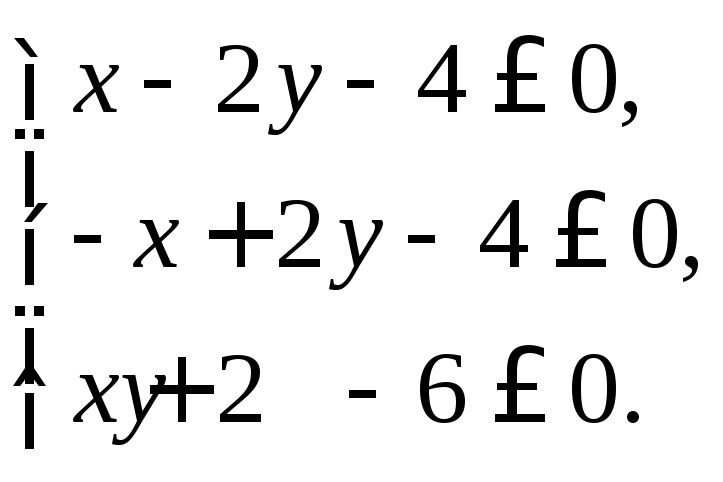
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 3

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

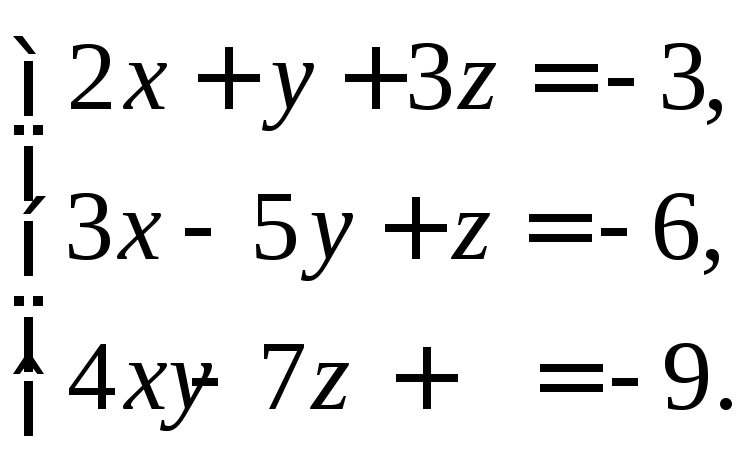
2. Найти множество решений системы линейных неравенств:

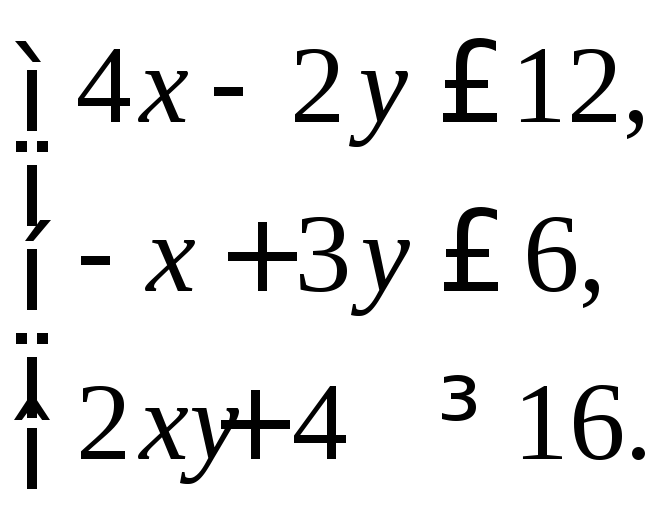
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 4

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

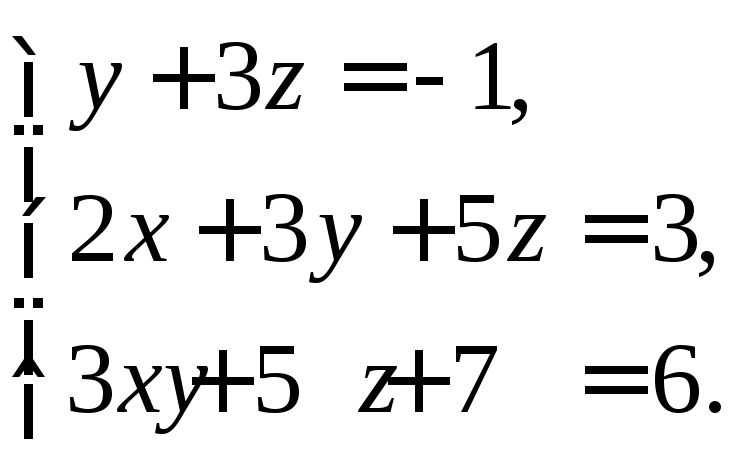
2. Найти множество решений системы линейных неравенств:

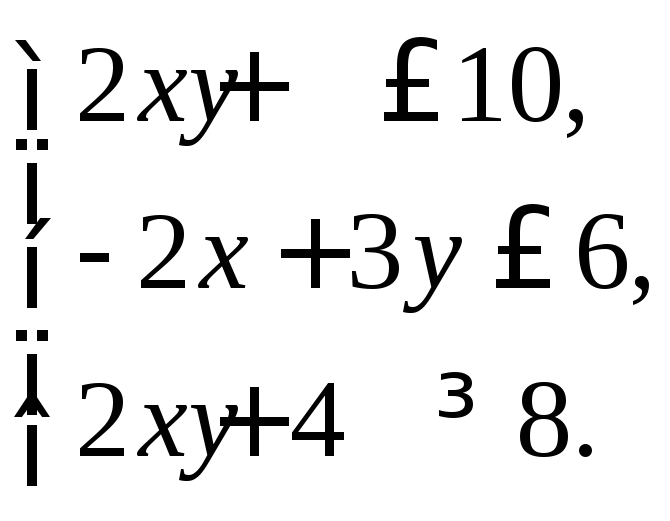
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 5

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

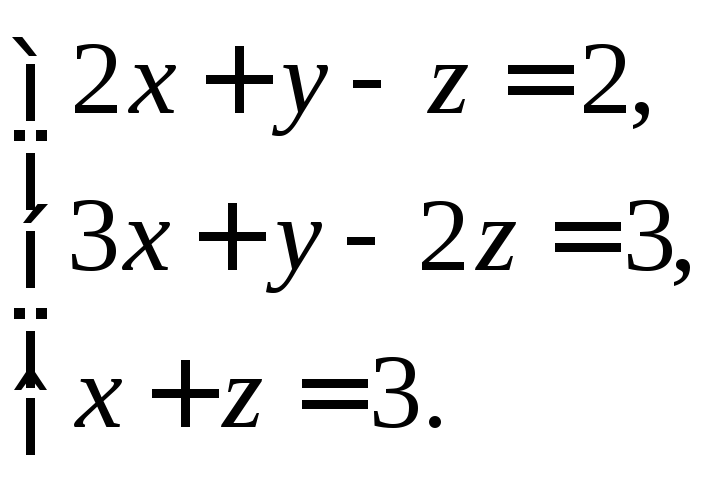
2. Найти множество решений системы линейных неравенств:

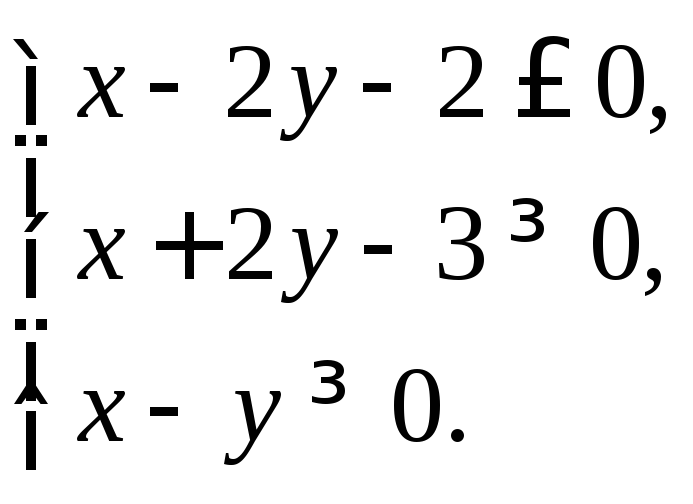
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 6

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

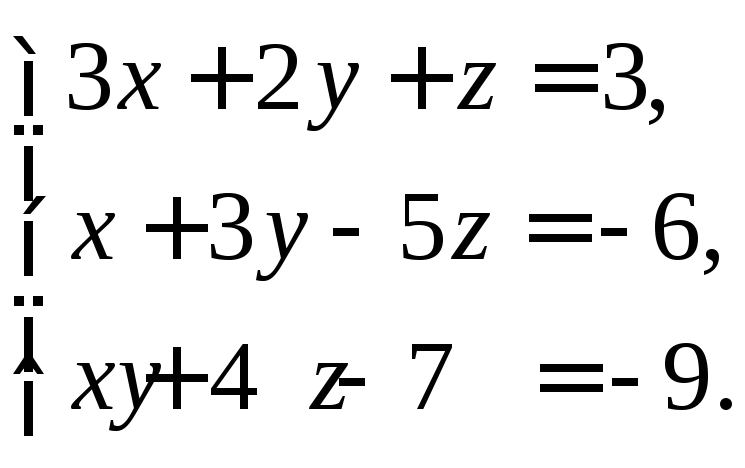
2. Найти множество решений системы линейных неравенств:

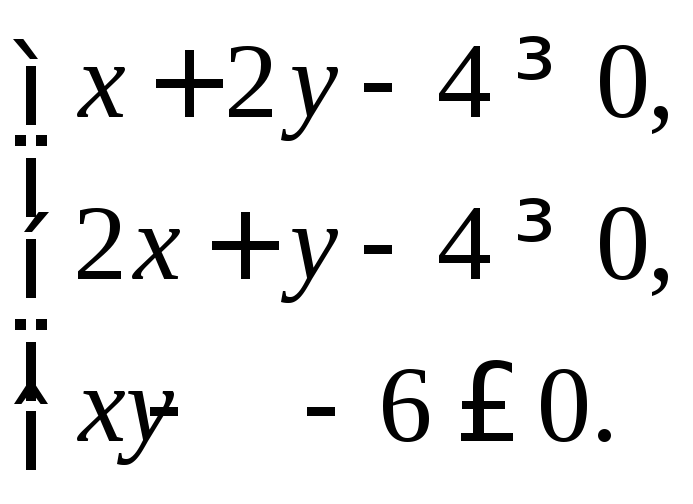
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 7

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

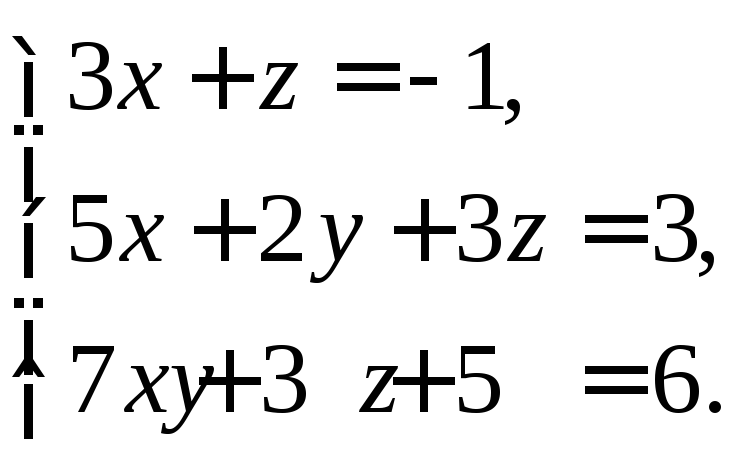
2. Найти множество решений системы линейных неравенств:

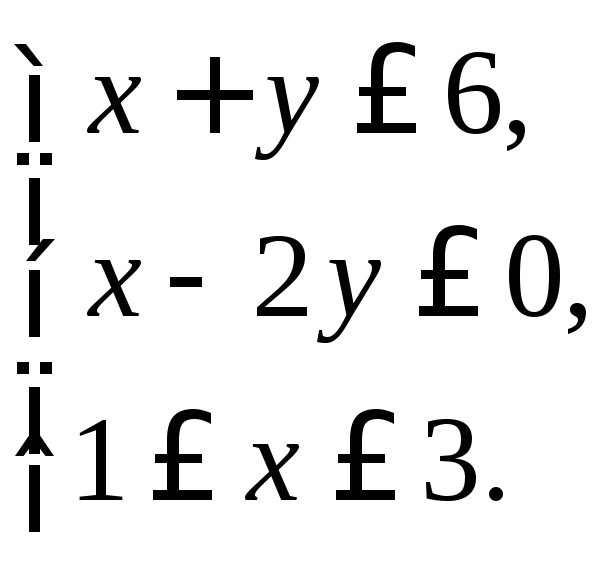
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 8

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

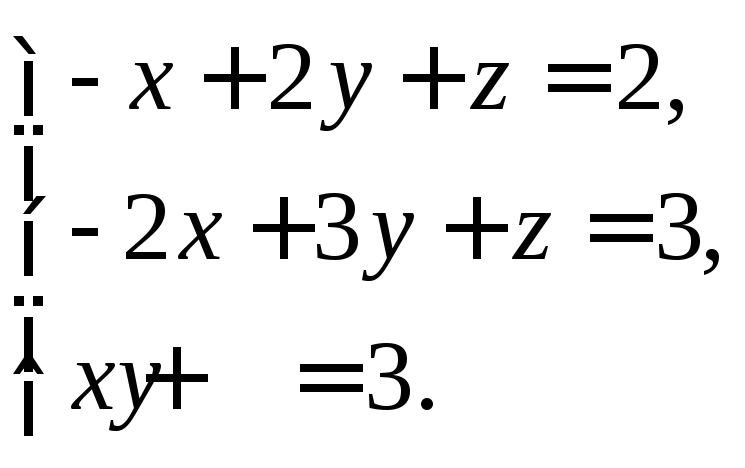
2. Найти множество решений системы линейных неравенств:

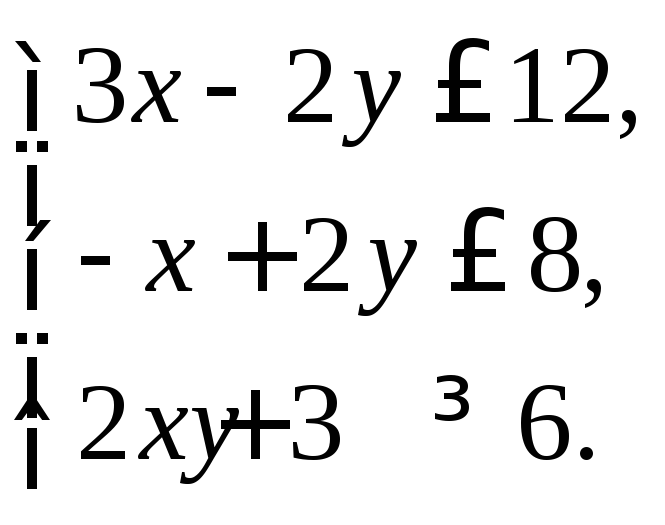
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

ВАРИАНТ 9

1. Решить систему линейных уравнений:

а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

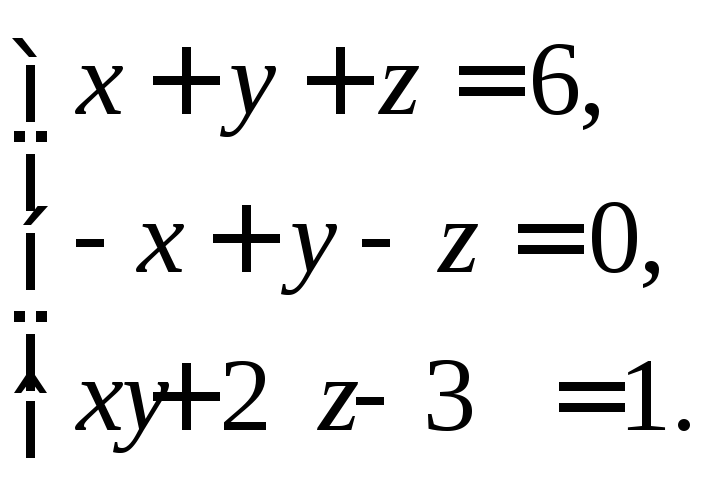
2. Найти множество решений системы линейных неравенств:

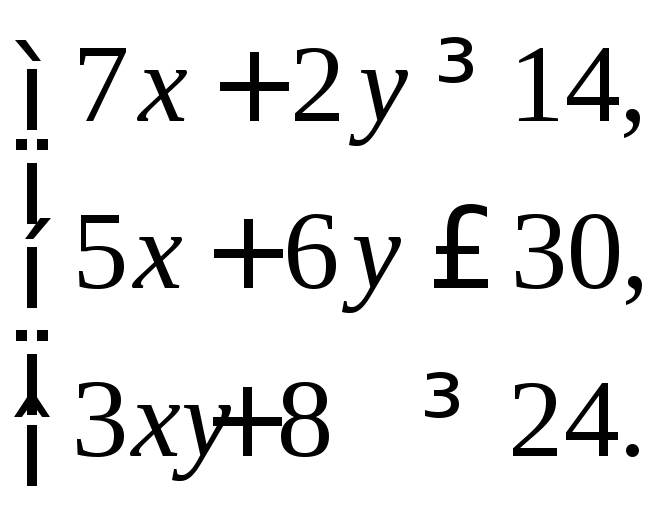
3. По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

4. Определить линейную зависимость системы векторов

5. Представить вектор как линейную комбинацию векторов

9Методические указания для выполнения

контрольной работы

Пример 9.1

Решить систему линейных уравнений:

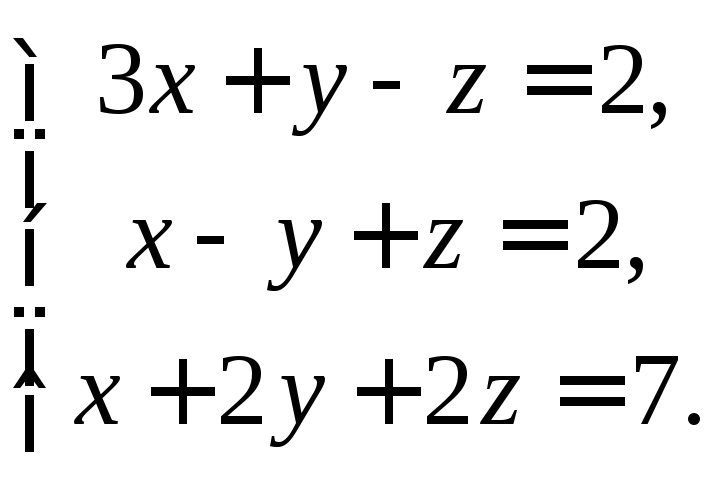
а) методом Крамера,

б) методом Гаусса,

в) матричным методом.

Метод Крамера

1. Найдем определитель системы:

.

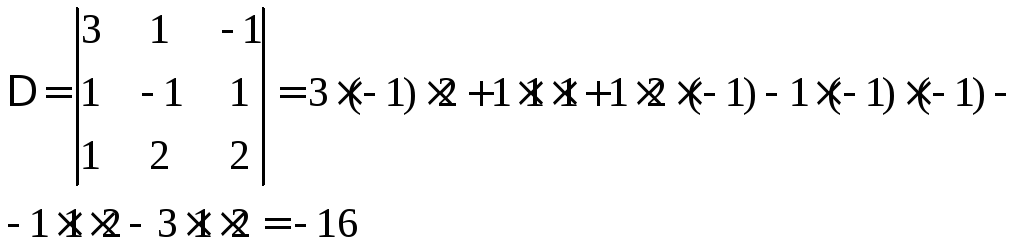2. Найдем вспомогательные определители.

Заменив первый столбец определителя системы на столбец свободных коэффициентов, получим определитель:

.

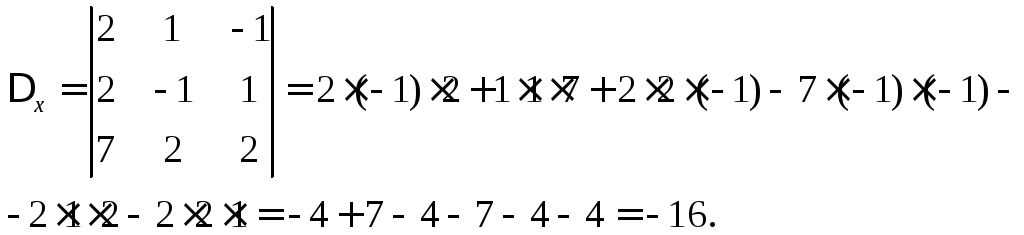Аналогично находим

.

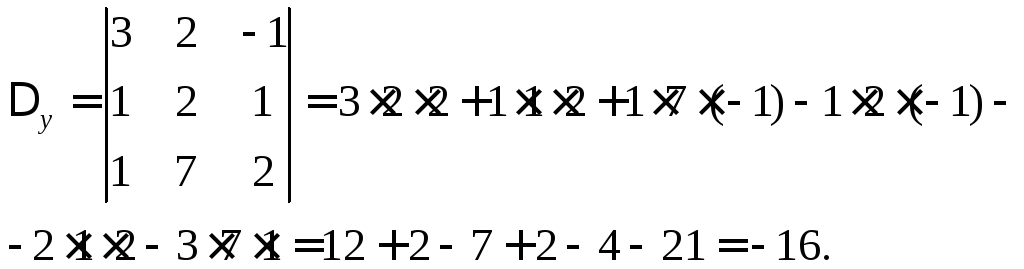
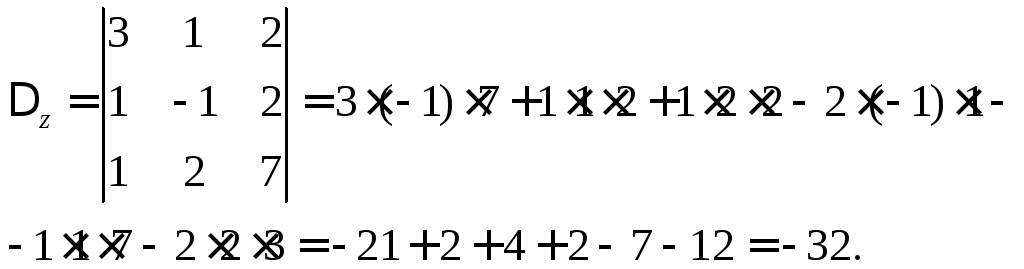3. Теперь по формулам Крамера найдем переменные

, ,.

5. Сделаем проверку решения. Подставим полученное решение в систему уравнений.

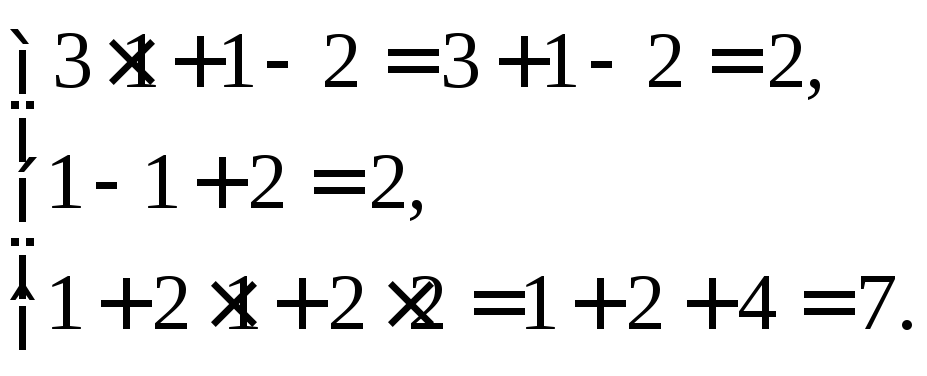
Ответ: (1, 1, 2).

Матричный метод решения

1. Найдем определитель системы:

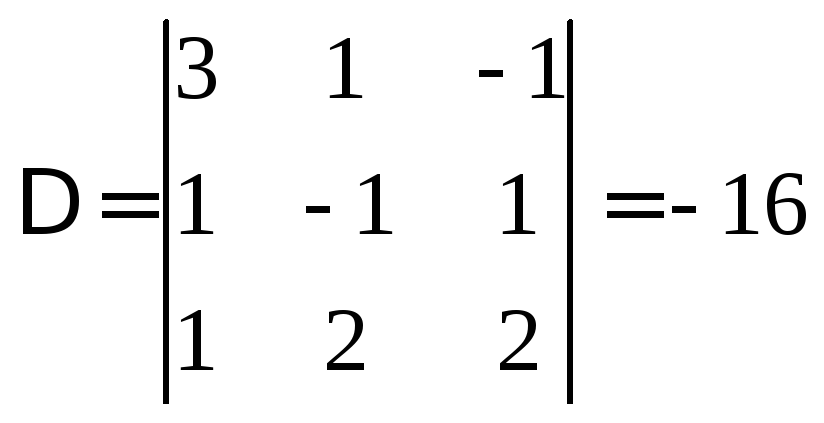
2. Составим матричное уравнение:

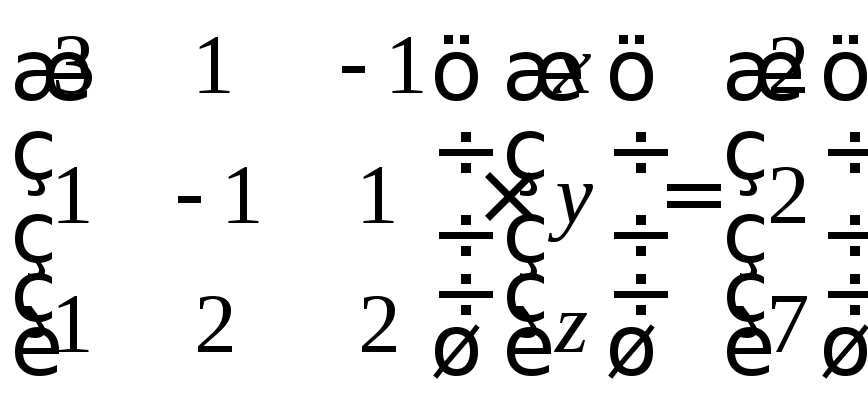
3. Найдем все алгебраические дополнения:

4. Построим обратную матрицу:

.

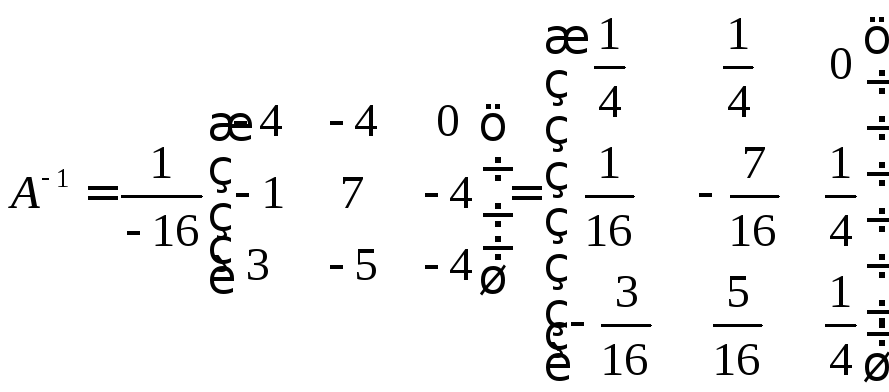5. Проверим обратную матрицу

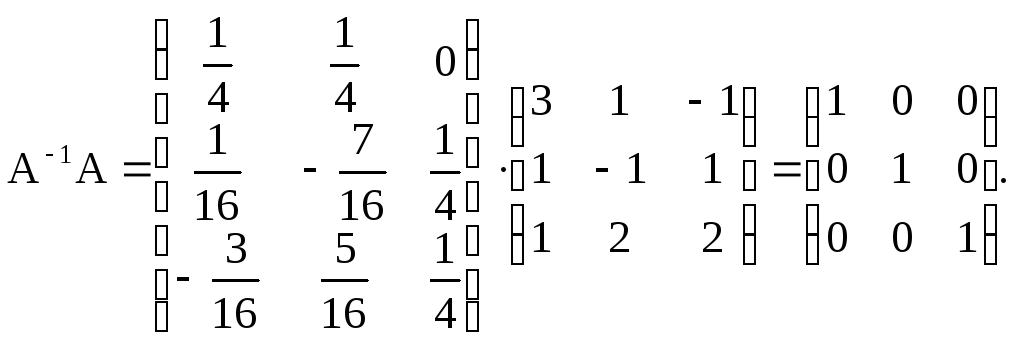
6. Найдем произведение матриц:

.

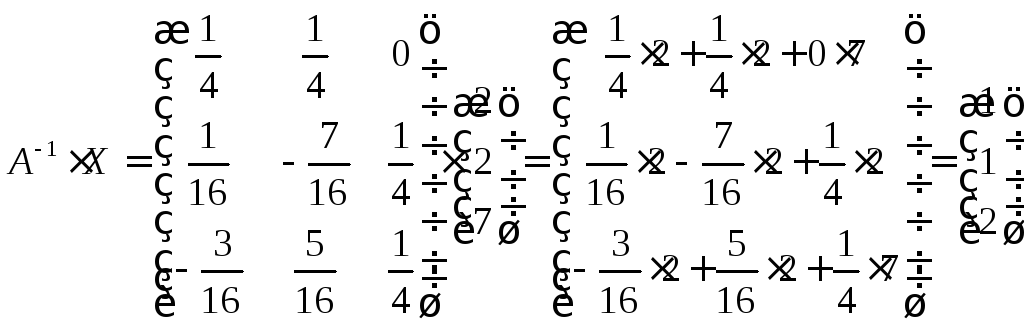Итак, имеем .

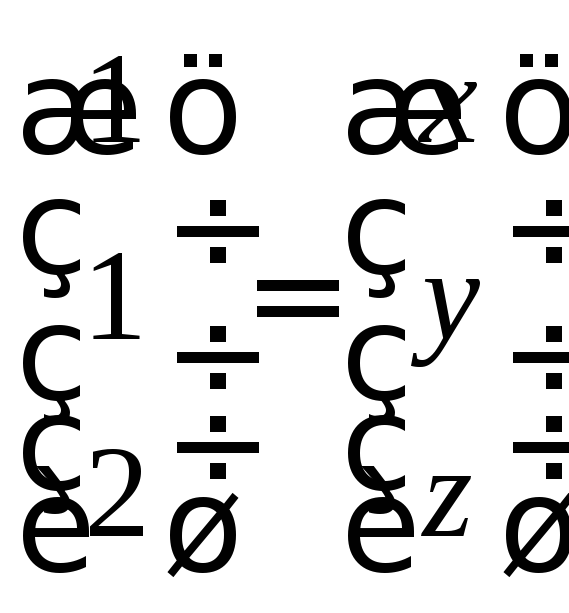Ответ: (1, 1, 2)

Метод Гаусса

Для удобства преобразований, составим расширен­ную матрицу из коэффициентов и свободных членов системы:

.

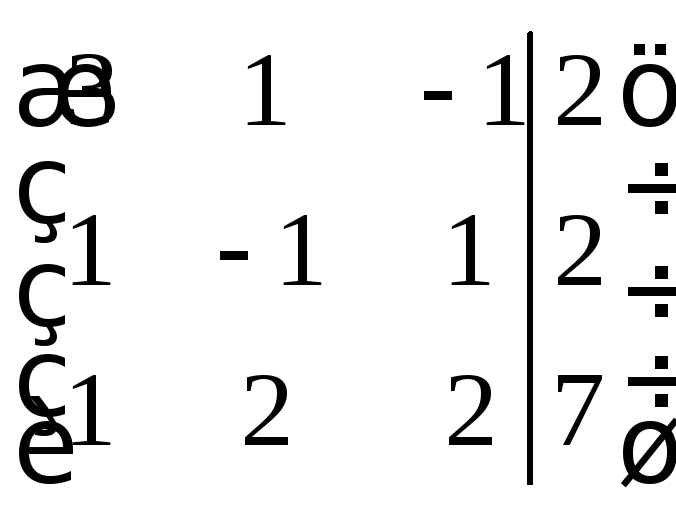Умножим 2-ую строку на (-3) и сложим с первой строкой; затем умножим 3-ю строку на (-3) и сложим с первой, получим матрицу

.

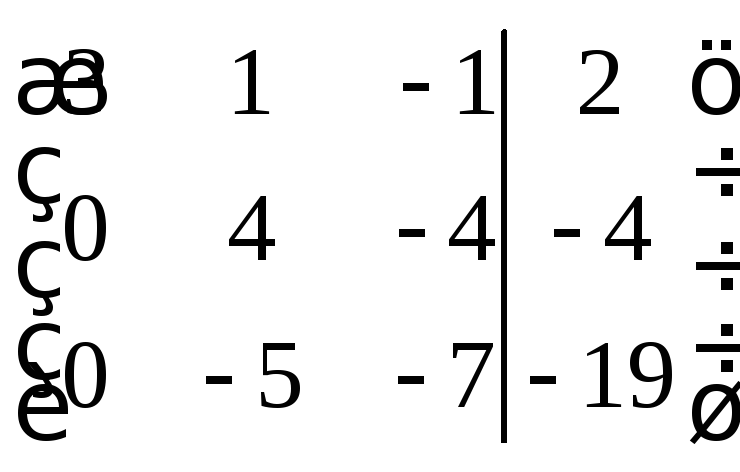Разделим коэффициенты второй строки на 4:

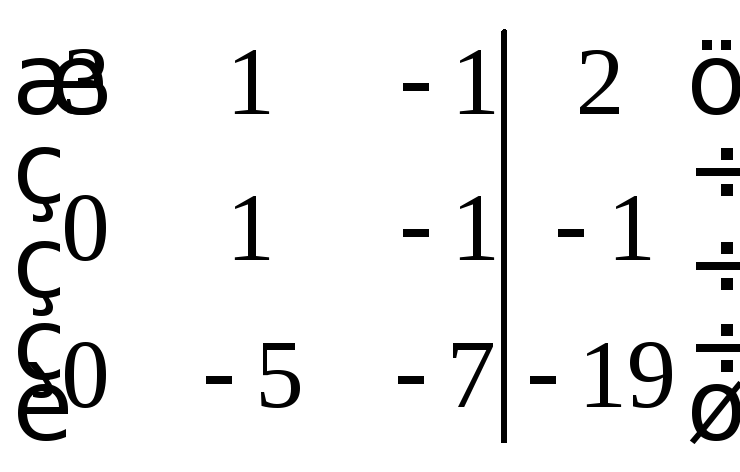
Теперь умножим 2-ую строку на 5 и сложим с третьей; получим

.

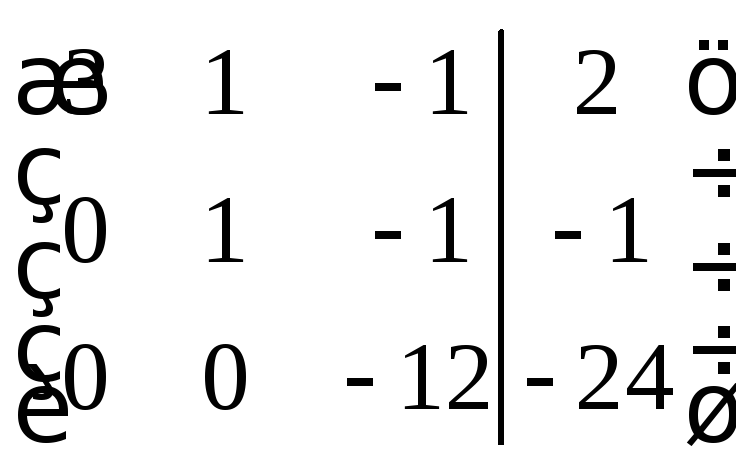Запишем полученные преобразованные уравнения:

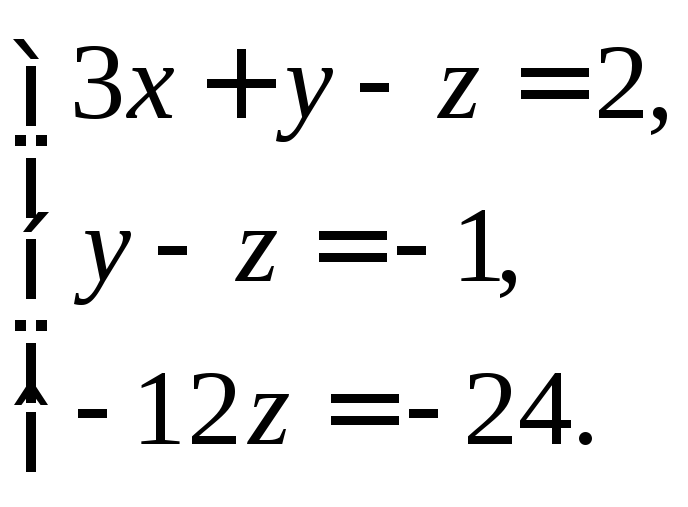
Теперь из 3-его уравнения находим . Подставив это значение во второе уравнение, получаем, откуда находим.

Подставив найденные значения ив первое уравнение, получим, откуда находим,.

Ответ: (1, 1, 2)

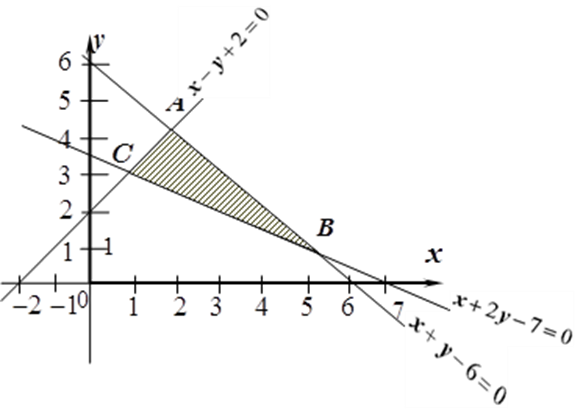
Пример 9.2 Найти множество решений системы линейных неравенств:

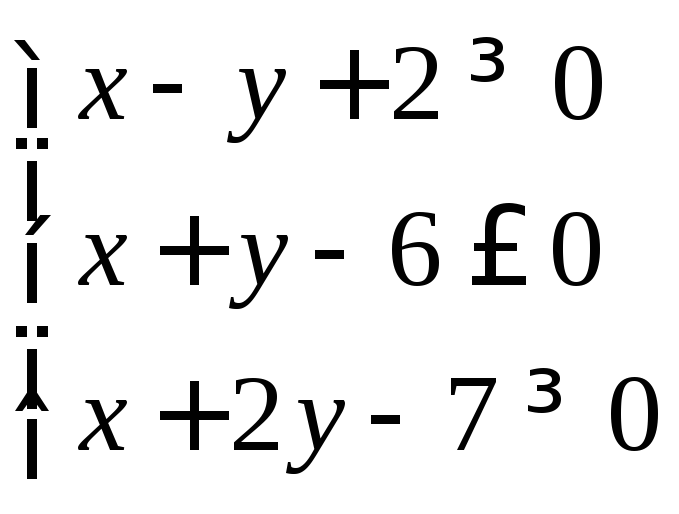
Решение.

Построим прямую . Для этого определим два произвольных решения этого уравнение, например (0, 2) и (1, 3). Отметим полученные значения на координатной плоскостиOXYи построим прямую.

Определим множество решения неравенства . Для этого подставим произвольную точку плоскости, через которую не проходит прямаяв неравенство и определим истинность полученного выражения. Например, подставив точку (0, 0), получим 20, что является истиной. Так как выбранная точка (0,0) расположена ниже прямой, следовательно, множеством решения будет являться полуплоскость лежащая ниже прямой.

Аналогично построим прямые ии определим множество решений соответствующих неравенств.

Множеством решений системы является общая часть решений всех неравенств, представляющая собою треугольник , изображенный на рисунке 9.1. При этом точки, лежащие на сторонах треугольника, в это множество включаются.

Рисунок 9.1 – Множество решений системы неравенств

Пример 9.3

По данным векторам и

а) найти вектора: ,

б) проверить ортогональность векторов.

Решение.

а) Для того чтобы найти вектор , необходимо умножить координаты векторана 2, координаты векторана 3 и сложить соответствующие координаты полученных векторов.

=(8, 6, -2)+(6, 3, 33)=(14, 9, 31).

Аналогично находим вектор :

=(4, 3, -1) – (4, 2, 22)=(0, 1, -23)

Ответ:=(14, 9, 37),=(0, 1, -27)

б) Для того, чтобы проверить ортогональность векторов, найдем скалярное произведение по формуле .

Если скалярное произведение векторов равно нулю, то вектора ортогональные.

,

следовательно, вектора и ортогональные.

Пример 9.4

Определить линейную зависимость векторов

_{Решение.}

_{Составим линейную комбинацию векторов}

_{Отсюда получим систему однородных уравнений:}

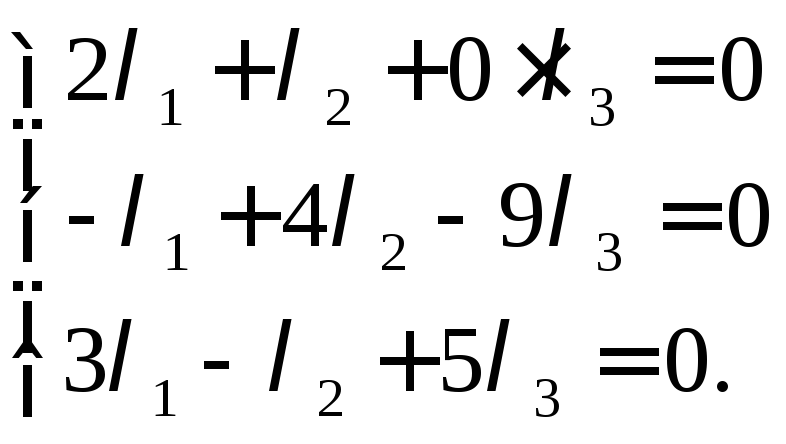
_{Для того чтобы система имела нетривиальное решение необходимо чтобы определитель матрицы системы был равен нулю.}

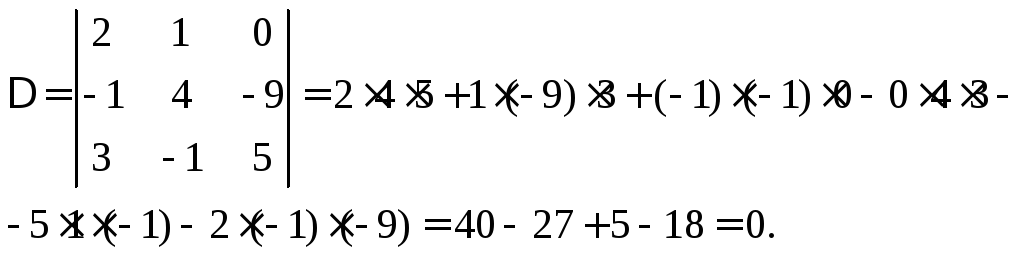
Итак, линейная комбинация векторов равна нулю, при , то есть система векторов линейно зависима.

_{Ответ: система линейно зависима.}

Пример 9.5

Представить вектор как линейную комбинацию векторов, ,.

1. Представим вектор как линейную комбинацию векторов ,,:.

.

2. Используя правила умножения вектора на число и сложения векторов получим равенство:

.

3. Используя условие равенства двух векторов получим систему линейных алгебраических уравнений:

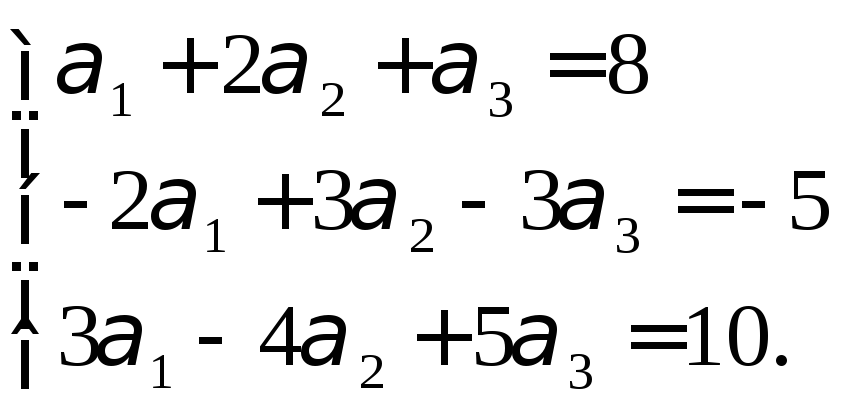
_{4. Решим эту систему любым из методов решения, например методом Гаусса.}

_{Выпишем расширенную матрицу системы}

_.

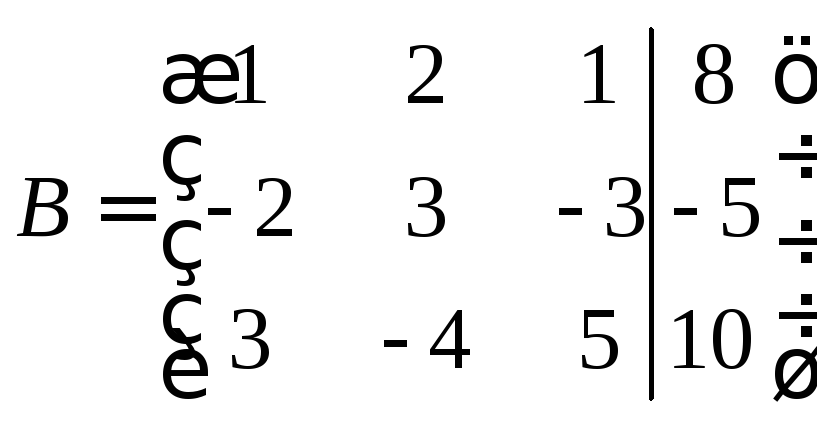_{Умножим первую строку на 2 и сложим со второй строкой, затем умножим первую строку на (-3) и сложим с третей строкой, получим матрицу}

_.

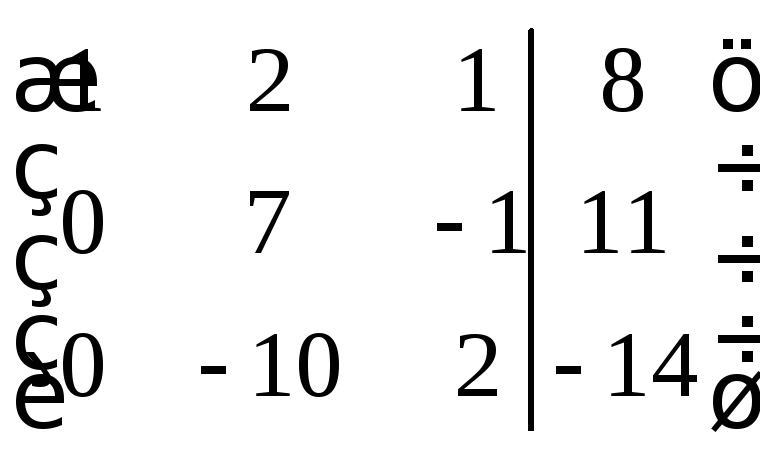Умножим вторую строку на 10 и сложим с третей строкой умноженной на 7.

.

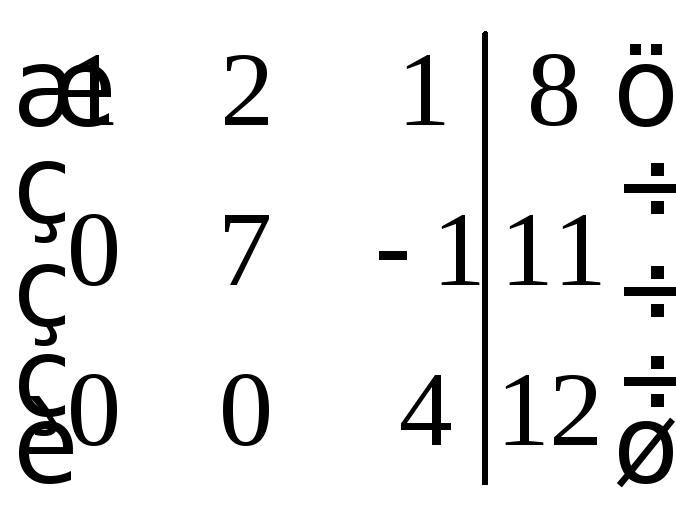Выпишем полученную систему и найдем значения .

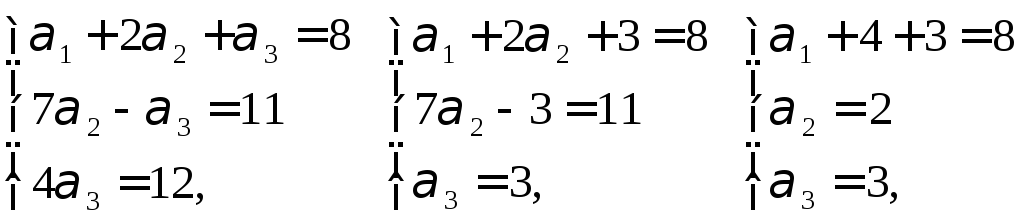
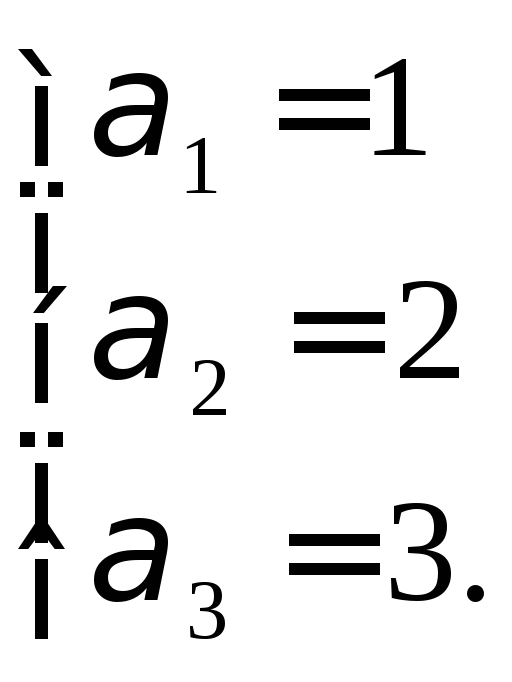
Ответ: