4 Система линейных уравнений

Линейные уравнения- это уравнения, в которых переменные имеют только первую степень и нет произведения переменных.

Система mлинейных уравнений сnнеизвестными записывается в виде:

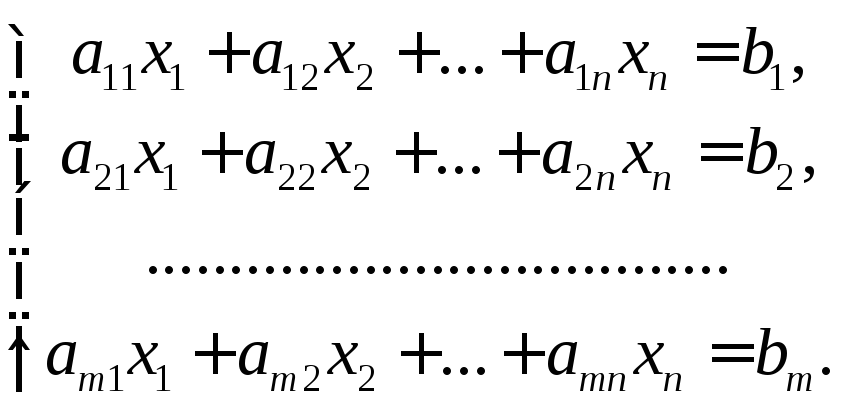(4.1)

В частном случае число уравнений и число переменных совпадают: m = n.

Решением системыявляется совокупностьnчисел, которые при подстановке их в уравнения (4.1) обращают их в тождество.

Если система (4.1) имеет хотя бы одно решение, она называется совместной; если нет ни одного решения, то системанесовместна.

Если совместная система имеет только одно решение, то она называется определенной. Если более одного решения, тонеопределенной.

Определитель, составленный из коэффициентов при переменных, называется определителем системы. Например, для системы двух уравнений с двумя неизвестными

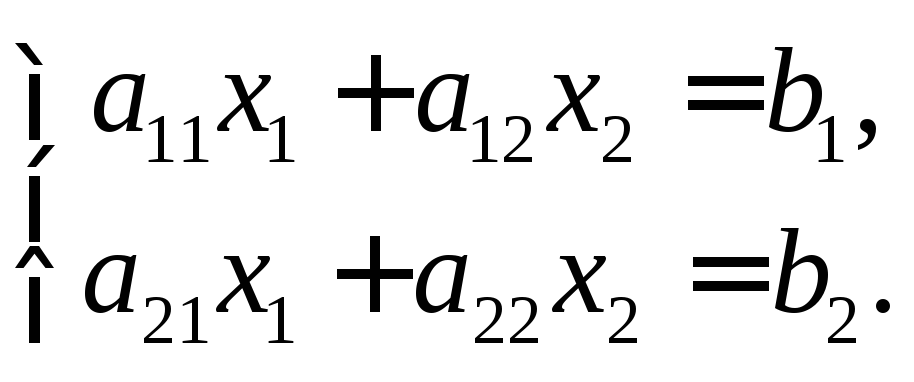(4.2)

определитель системы имеет вид

.

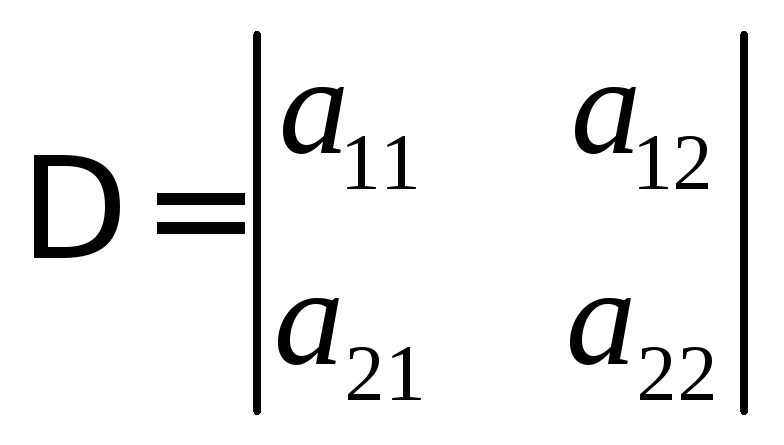Если определитель системы не равен нулю 0, то система имеет единственное решение.

Для решения системы n- линейных уравнений сn- неизвестными существует несколько методов.

4.1 Метод Крамера

При использовании этого метода решение системы находится по формулам

..., (4.3)

где -определитель системы,

_i - определитель, в котором элементыi-го столбца определителя системы заменяются соответствующими свободными членами уравнений системы.

Например, для системы (4.2) имеем

, .

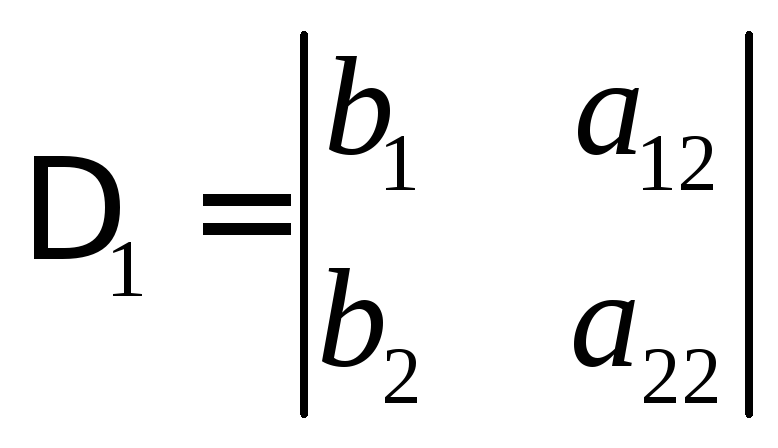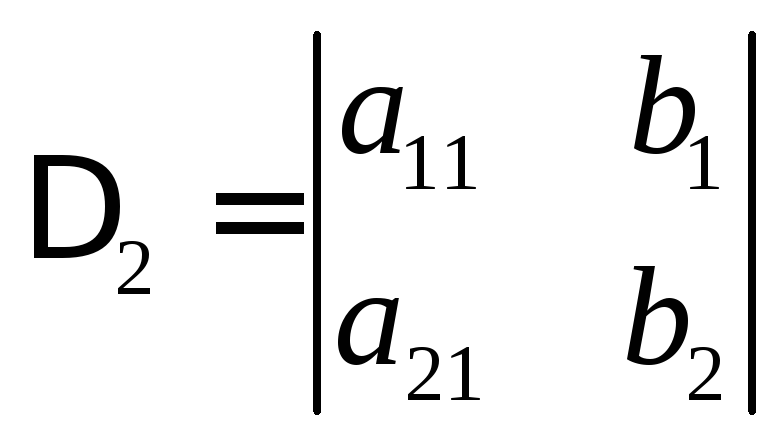При решении системы следует иметь в виду следующее:

Если =0, но хотя бы один из определителей₁,₂, ...,_n не равен нулю, то система несовместна.

Если =0 и все определители₁,₂,...,_nравны нулю , то система или несовместна или имеет бесконечно много решений, если существует хотя бы одно решение.

Пример 4.1

Решить систему уравнений

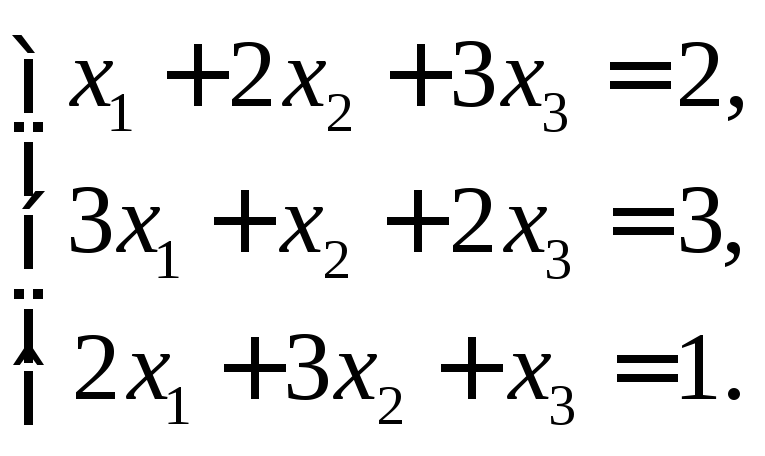
Найдем определитель системы:

.

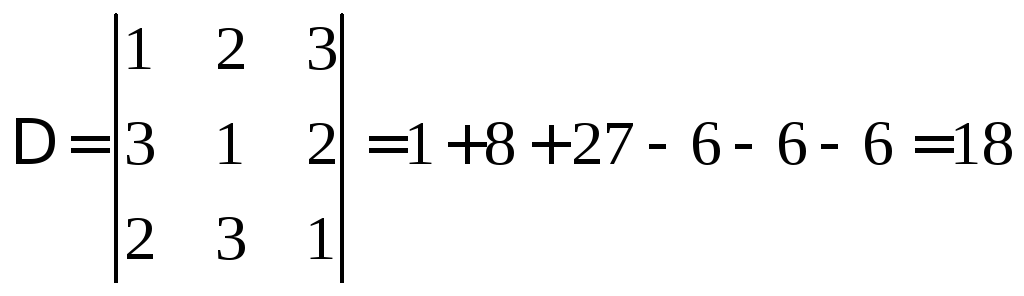Найдем вспомогательные определители

.

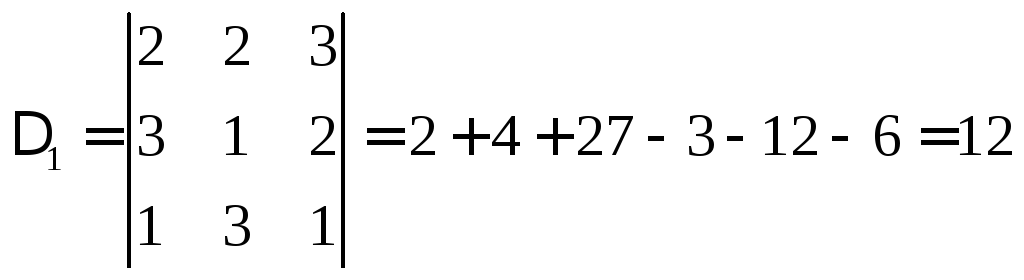Аналогично находим

, .

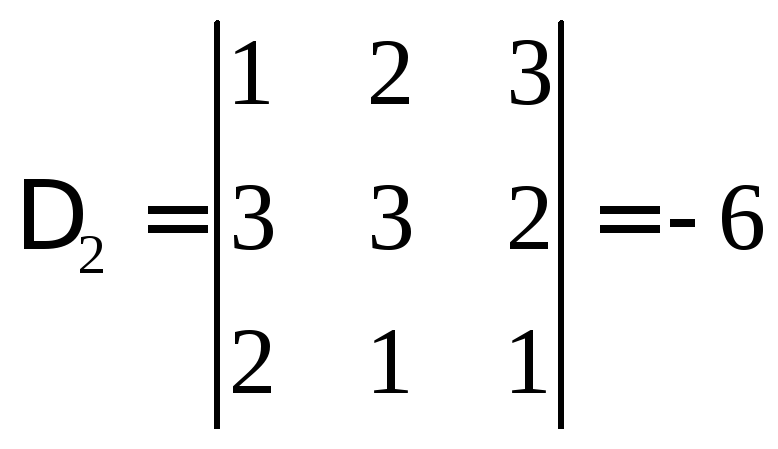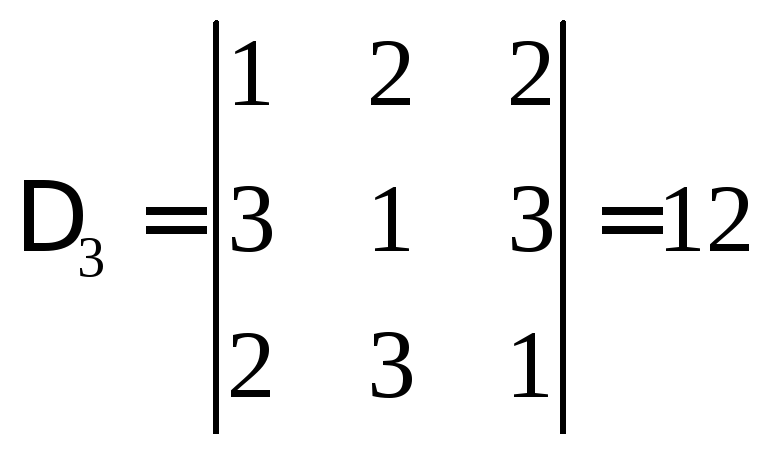Теперь по формулам Крамера (4.3) найдем переменные

,

,

.

Итак, данная система имеет единственное решение:

.

4.2 Матричный метод решения

Рассмотрим этот метод на примере системы трех линейных уравнений:

эту систему можно представить в матричной форме:

АХ=В, (4.4)

где

, ,.

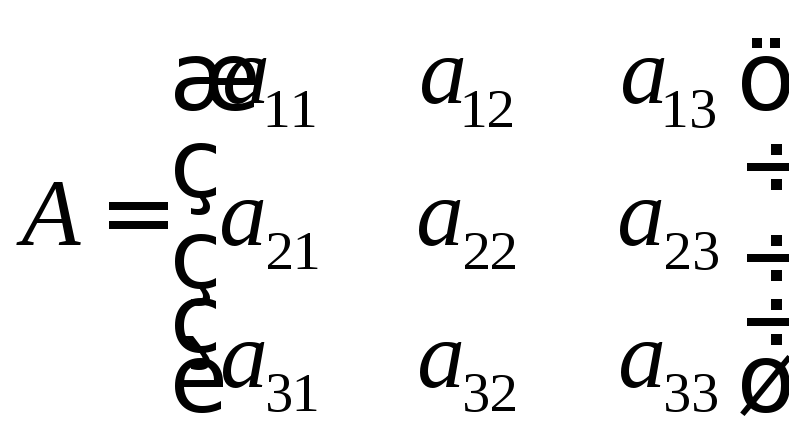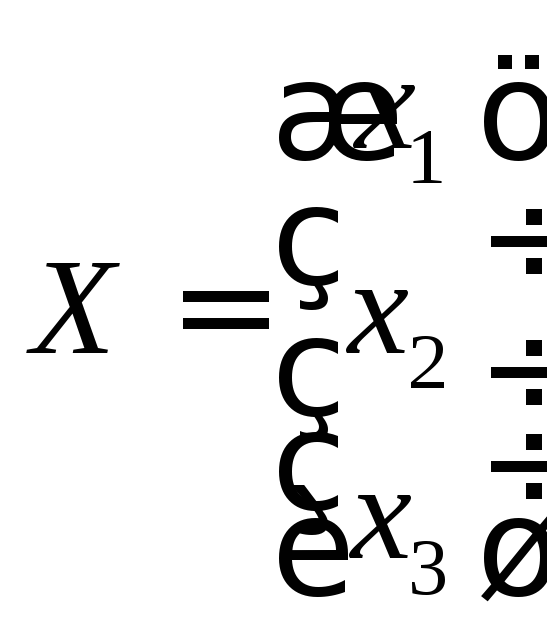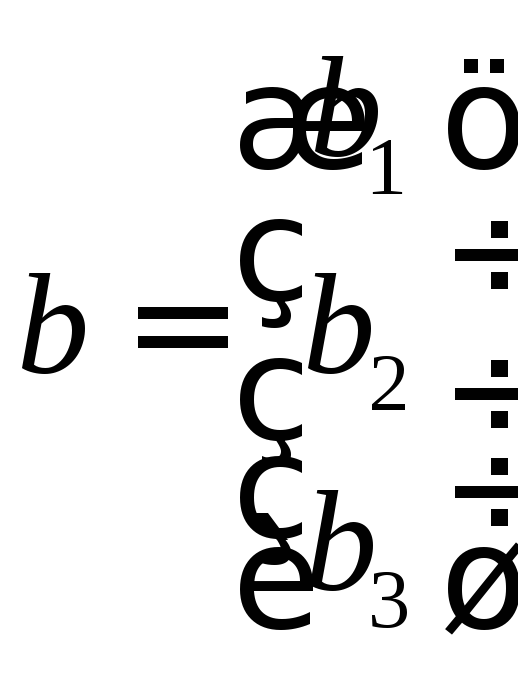Как видно, А -это матрица, составленная из коэффициентов при перемененных,В- матрица - столбец из свободных членов уравнений,Х- матрица - столбец из переменных.

Решая матричное уравнение (4.4), находим

Х=А^-1В,

где А^-1- обратная матрица.

Итак, чтобы найти решение системы, нужно найти обратную матрицу А^-1и умножить ее на матрицуВ.

Пример 4.2

Решить систему матричным способом

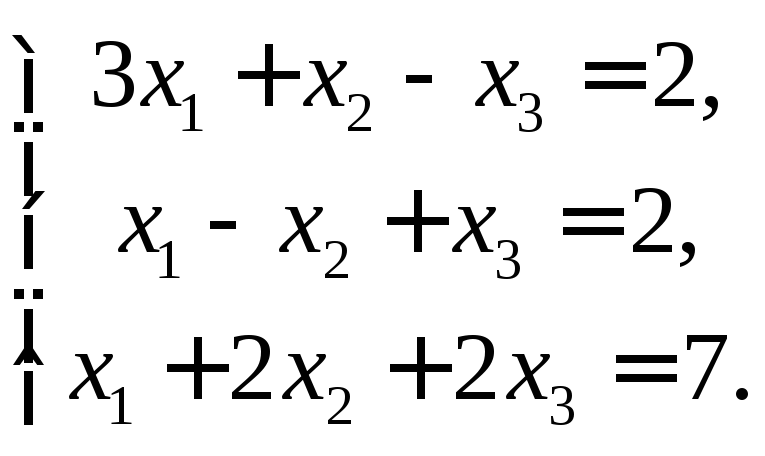
Найдем определитель системы:

.

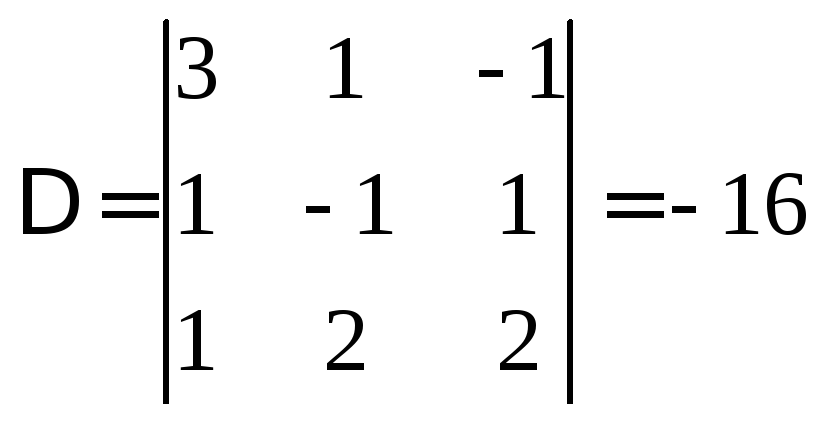Составим матричное уравнение:

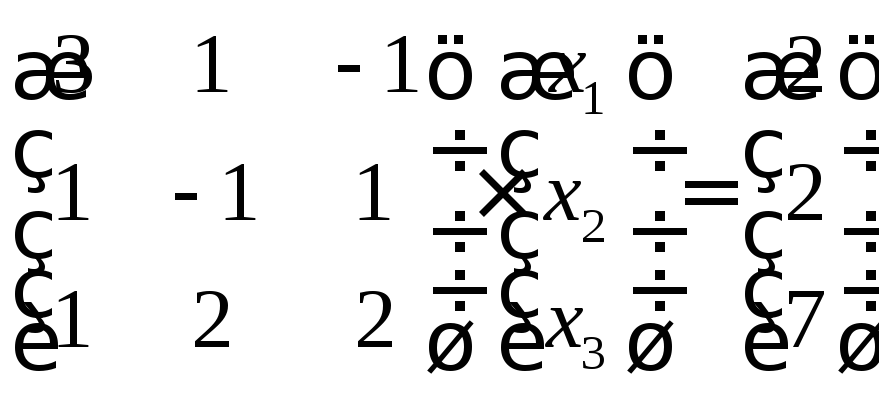
Найдем обратную матрицу. Для этого сначала найдем алгебраические дополнения:

, ,,

, ,,

, ,.

Построим обратную матрицу:

.

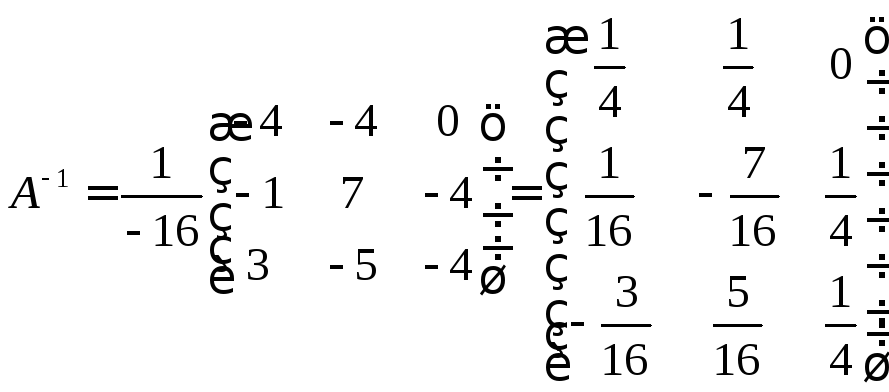Теперь найдем произведение матриц:

.

Итак, имеем

.

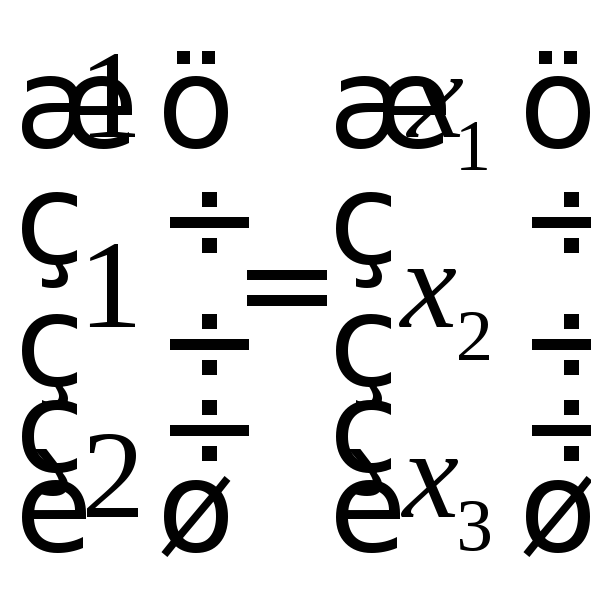Отсюда, х₁=1,х₂=1,х₃=2.

4.3 Метод Гаусса

Этот метод решения системы линейных уравнений заключается в последовательном исключении переменных из уравнений для того, чтобы в одном из уравнений осталось одно неизвестное. Покажем, как применяется этот метод на примере.

Пример 4.3

Решить систему уравнений

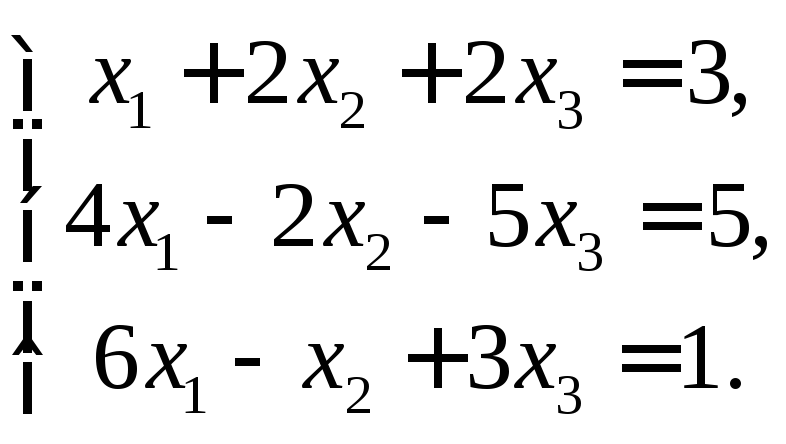
Для удобства преобразований, составим расширенную матрицу из коэффициентов и свободных членов:

.

Умножим 1-ую строку на (-4) и сложим со второй строкой; затем умножим 1-ую строку на (-6) и сложим с третьей, получим

.

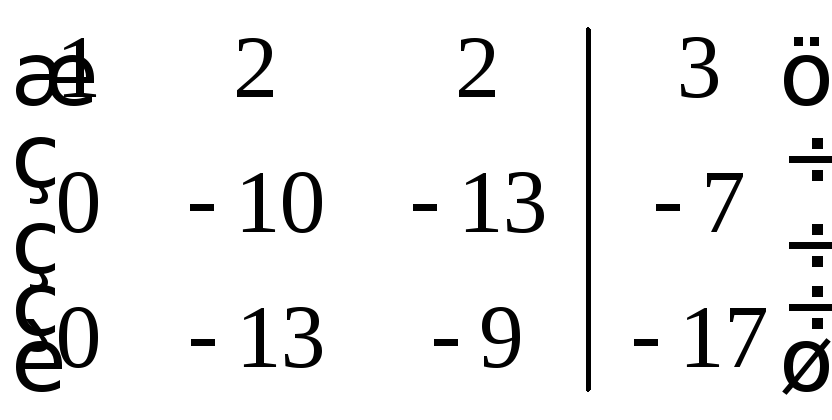Теперь умножим 2-ую строку на и сложим с третьей; получим

.

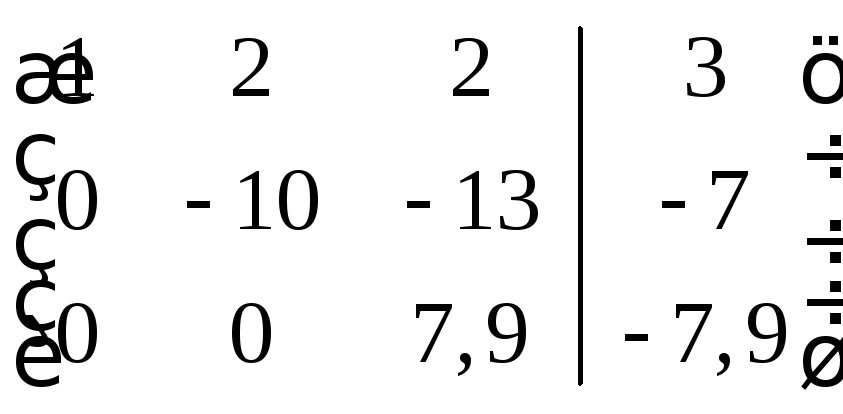Запишем полученные преобразованные уравнения:

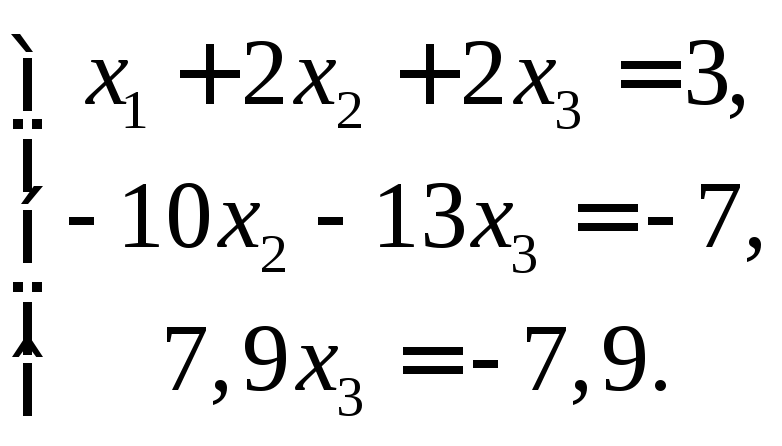
Теперь из 3-его уравнения находим, из 2-го уравнения находимх₂=2, из 1-го уравнения имеемх₁=1. Итак, решение системых₁=1,х₂=2,.

Как видно из данного примера, преобразования уравнений нужно делать так, чтобы элементы матрицы, расположенные ниже диагонали оказались равны нулю.

Пример 4.4

Найти решение системы

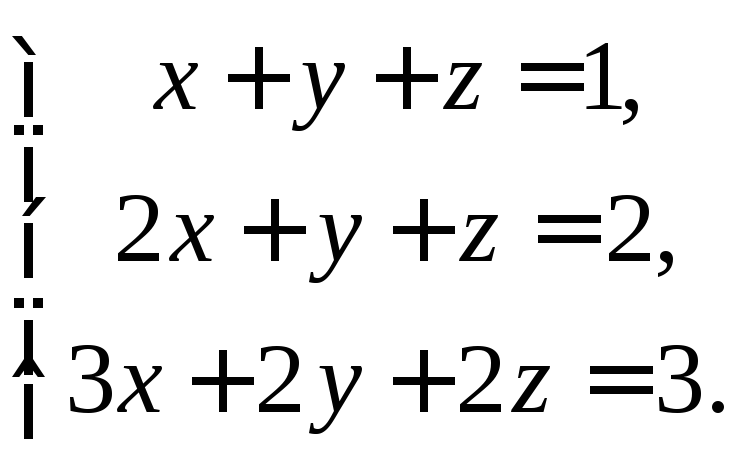
Вычислим определитель системы

.

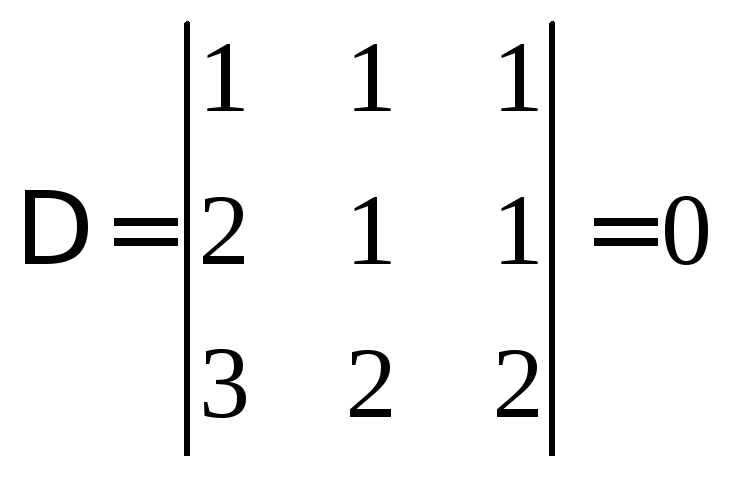Вычислим дополнительные определители по формулам Крамера

, ,.

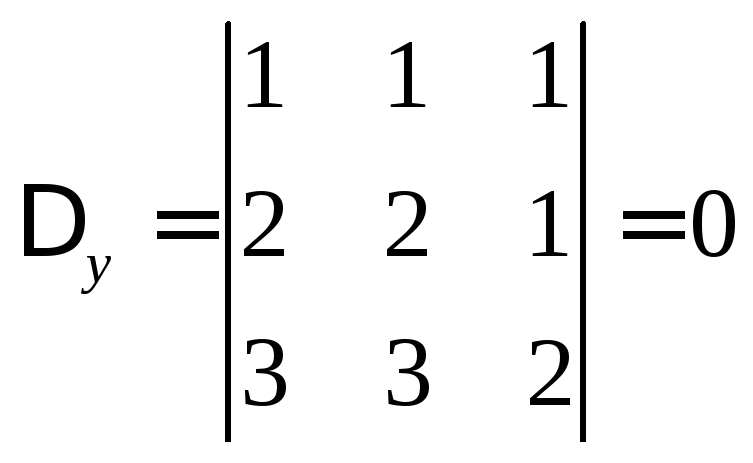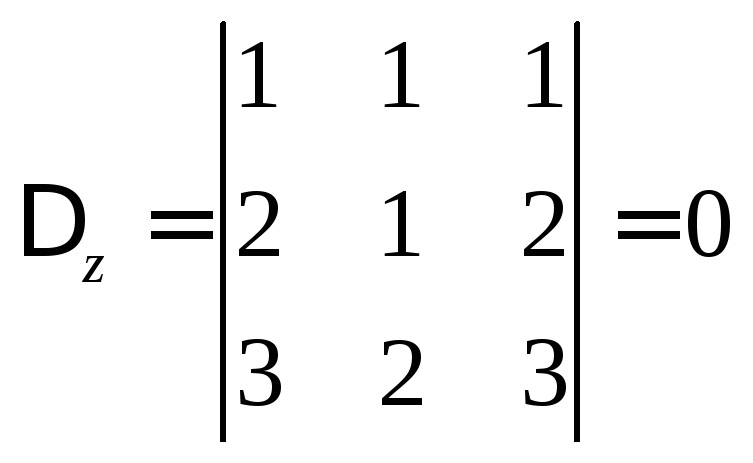Все эти определители равны нулю, так как имеют два одинаковых столбца. Таким образом, единственного решения у системы нет. Полагая х=1, из первого уравнения получим.

Итак, у системы бесконечно много решений , гдеС- любое значение.