6 Пример использования системы линейных уравнений в экономике

Пример 6.1

Для выполнения плана товарооборота, составляющего Q(у.е.), фирме нужно продать товары трех видов в количестваха_11, а₁₂,а₁₃соответственно. Если продать эти товары в количестваха_21,а₂₂,а₂₃, то план товарооборота будет перевыполнен в два раза. Если же товары продать в количестваха₃₁,а₃₂,а₃₃, то план будет выполнен лишь на 50%. Определить стоимость единицы товара каждого вида.

Обозначим стоимость единицы товара каждого вида соответственно через х, у, z. Это условие можно записать в виде матрицы - столбца:

.

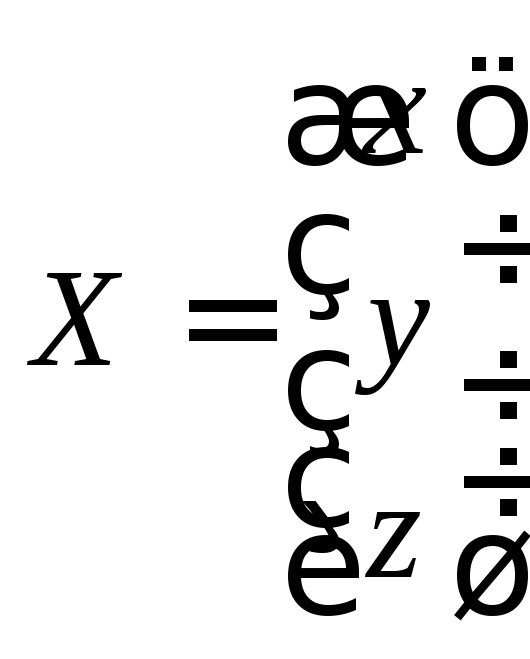Количество товара планируемого к продаже в трех случаях можно представить в виде квадратной матрицы

.

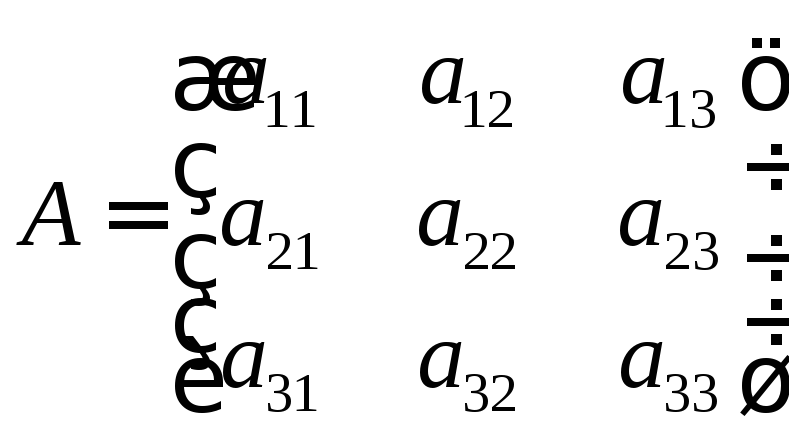Выручку от продажи также можно представить как матрицу:

.

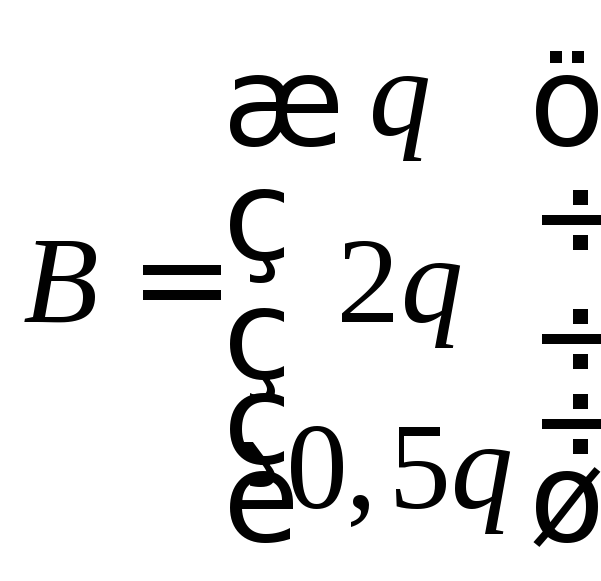Тогда математической моделью задачи будет являться матричное уравнение

АХ=В,

или система трех линейных уравнений

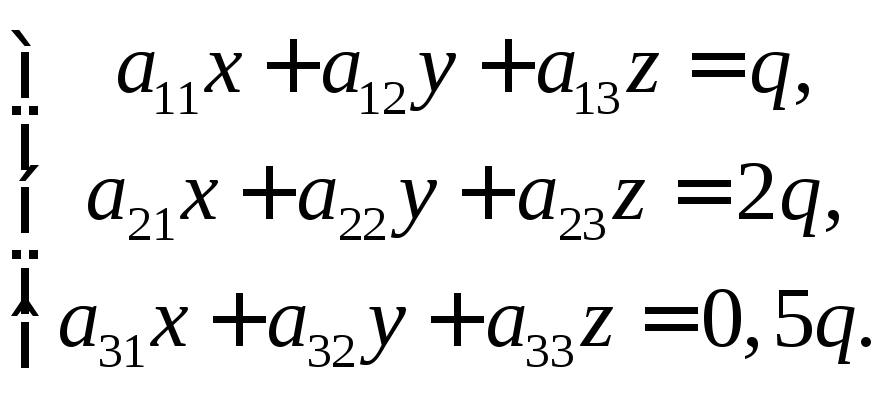
Таким образом, решение задачи сводится к нахождению решения системы трех линейных уравнений. При конкретных числовых значениях это решение можно найти любым из трех методов.

Пример 6.2

С двух заводов поставляют автомобили для двух хозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, второй – 150. Затраты на перевозку машин с заводов в первое хозяйство составляют 15 ден.ед и 20 ден ед., во второе - 8 ден.ед и 25 ден.ед. Минимальные затраты на перевозку равны 7950 ден.ед. Найти оптимальный план перевозки машин.

Обозначим через - количество машин, поставляемых сi- го заводаj- ому хозяйству. Получаем систему уравнений

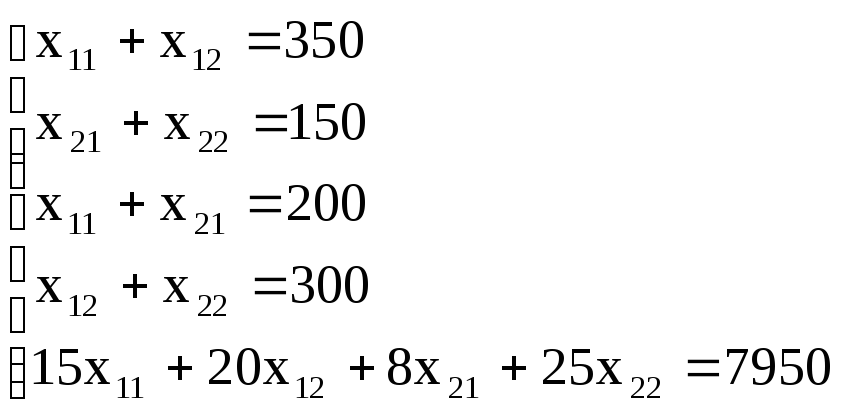
Решив эту систему методом Гаусса, получим

7 Понятие вектора. Система векторов

Векторомназывается упорядоченный набор изnдействительных чисел.

В результате линейных операций над векторами (сложения, вычитания, умножения на число) получается новый вектор

Число равное называетсямодулем или длиной вектора.

Пусть даны два вектора и

Скалярным произведениемдвух векторов называется число равное сумме произведений соответствующих координат векторов.

Если скалярное произведение равно нулю, то вектора ортогональны.

В двумерном и трехмерном пространствах вектор можно представить геометрически как отрезок имеющий направление.

Пусть даны два вектора

Необходимым в достаточным условием коллинеарности векторов является пропорциональность их соответствующих координат:

Скалярным произведением геометрических ненулевых векторов называется произведение их модулей на косинус угла φ между ними:

Косинус угла между ненулевыми векторами может быть вычислен по формуле

Множество всех векторов пространства образует векторное пространство (линейное пространство).

В векторной алгебре большое значение имеет понятие линейной зависимости векторов. Система векторов называетсялинейно зависимой, если существуют числа , из которых хотя бы одно отлично от нуля, такие, что линейная комбинация из векторов будет равна нулю, то есть справедливо равенство

Система векторов называется линейно независимой, если линейная комбинация их равна нулю, когда все коэффициенты равны нулю.

На плоскости существует не более двух, а в трехмерном пространстве не более трех линейно независимых векторов.

Для векторного пространства вводится понятие базис.

Базисом n - мерного пространства называется любая система из n линейно независимых векторов.

Любой вектор a единственным образом представляется в виде линейной комбинации векторов базиса b, c, d

Два вектора равнытогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе.

Пример 7.1

Выяснить являются ли вектора a₁ = (2,0), a₂ = (0,3) линейно зависимыми.

Решение

Составим линейную комбинацию . Подставим координаты заданных векторов.. Отсюда

Это равенство возможно лишь при значениях , т.е. вектора линейно независимы.

Пример 7.2

Разложить вектор d в базисе a,b,c, если известно, что

a= (1,0,0), b = (1,1,0), c = (1,1,1), d = (2,0,-1).

Решение

Представим вектор d как линейную комбинацию векторов a,b,c.

Подставим координаты заданных векторов, имеем

Отсюда приравнивая соответствующие координаты, получим

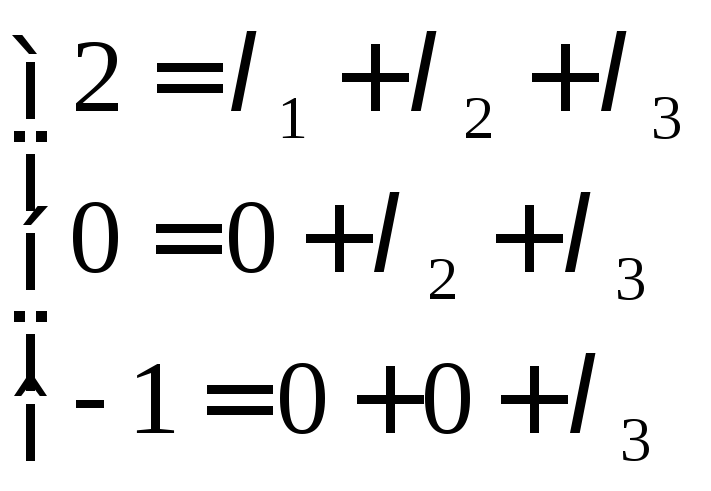
Решением системы является

Итак,