4.5 Однородные системы линейных уравнений

Система называется однородной, если все ее свободные члены равны нулю.

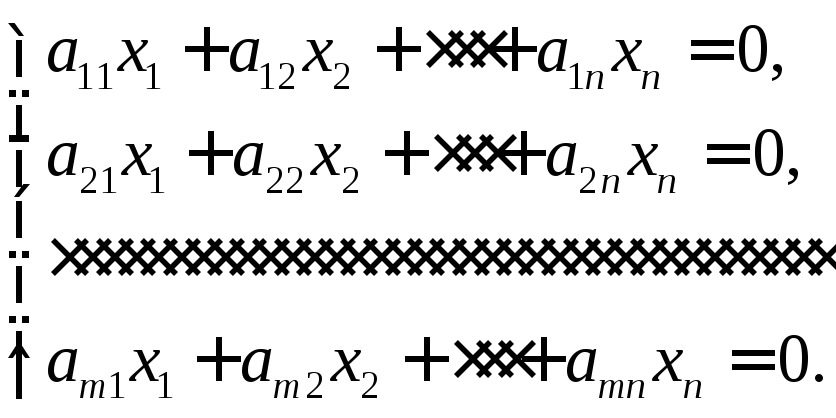
В этом случае система всегда совместна, т.к. имеет нулевое (тривиальное) решение.

Рассмотрим случаи, когда система имеет другие решения.

Теорема

Однородная система имеет ненулевое решениетогда и только тогда, когдарангматрицы Аменьше числа n(переменных)

.

Если (n=m) число уравнений равно числу неизвестных, то система имеетненулевое решениетогда и только тогда, когдаопределительсистемы равен нулю.

Пример 4.6

Исследовать систему

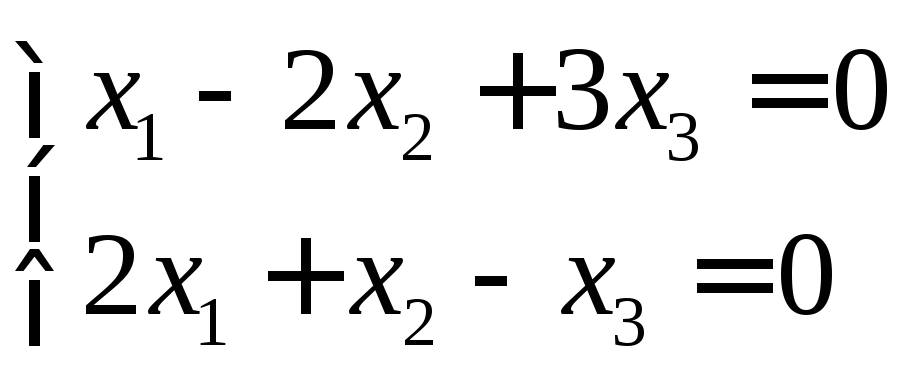
Решение: Составим матрицу системы

Из 2-ой строки вычтем 1-ую умноженную на 2, получим

Отсюда, , а n=3 т.е..

Следовательно, система имеет нетривиальное решение

Перепишем систему в виде

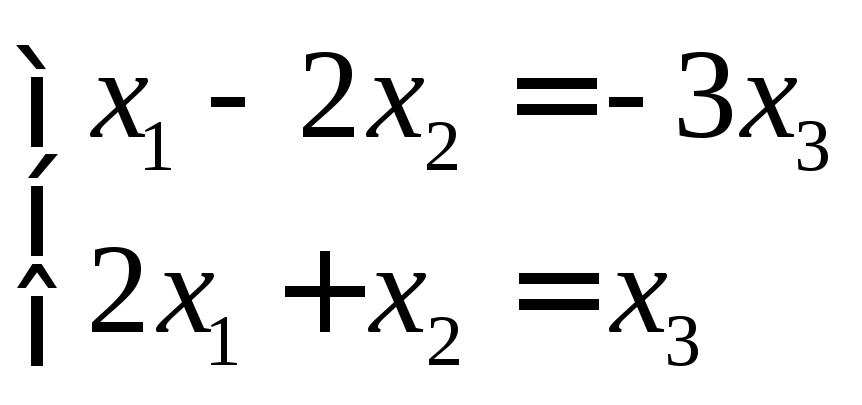
Положим , тогда

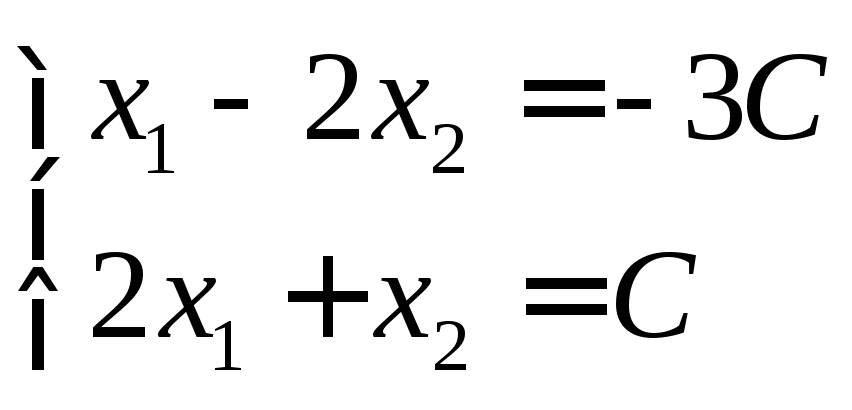
Отсюда

,

множество решений системы имеет вид

5 Системы линейных неравенств

В прикладных задачах часто приходится иметь дело с линейныминеравенствами, которыми называются выражения вида

или

. (5.1)

Линейное неравенство с двумя переменными имеет множество решений.

Геометрически каждое решение неравенства (5.1) можно представить как точку на плоскости . Тогда множеством решений или, иначе говоря,областью решений неравенстваявляется полуплоскость, расположенная выше или ниже прямой, описываемой уравнением.

Если задана система линейных неравенств с двумя переменными:

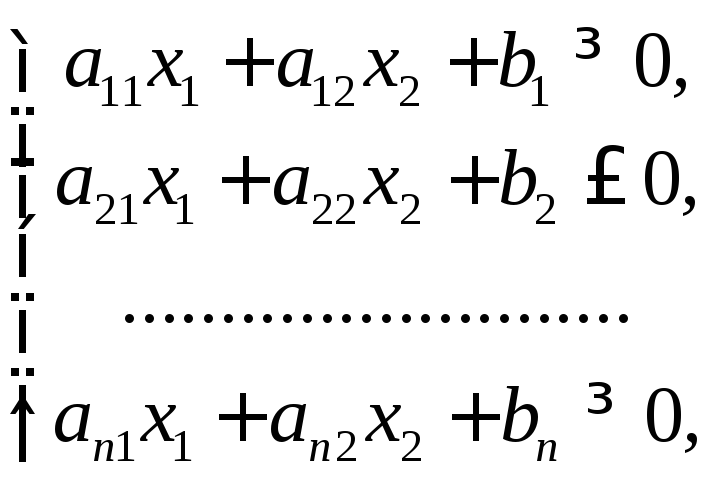(5.2)

то областью решений будет служить некоторый многоугольник, образованный пересечением полуплоскостей, соответствующих области решения каждого неравенства системы.

Заметим, что область решений системы (5.2) может быть и неограниченной, и пустой, когда система неравенств противоречива.

Пример 5.1

Найти область решений неравенства

. (5.3)

Построим прямую

(5.4)

н

0

а плоскостиоху. Для этого найдем точки пересечения прямой с осями: имеем прих=0у=2; приу=0х= -5

Решением уравнения (5.4) являются точки, принадлежащие этой прямой. Теперь рассмотрим строгое неравенство

2х- 5у+ 100 . (5.5)

Для того, чтобы выяснить какая полуплоскость служит областью решения этого неравенства, решим его относительно переменной у:

.

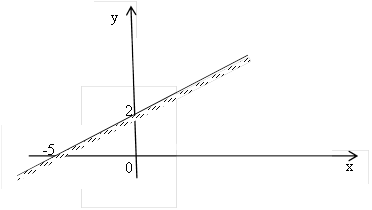
Отсюда следует, что областью решения неравенства (5.5) является полуплоскость, расположенная ниже прямой (5.4) (показано штрихами вниз на рисунке 5.1).

Рисунок 5.1- Область решения неравенства

Другой способ нахождения области решения неравенства (5.5) заключается в использовании контрольной точки. Обычно за нее берется начало координат (0,0). Подставляя х=0 иу=0 в неравенство (5.5), получим 100. Так как полученное выражение справедливо, то точка (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой (5.4), включая и прямую.

Пример 5.2

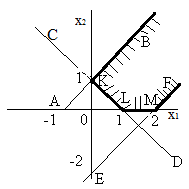
Найти множество решений систем линейных неравенств и найти координаты угловых точек.

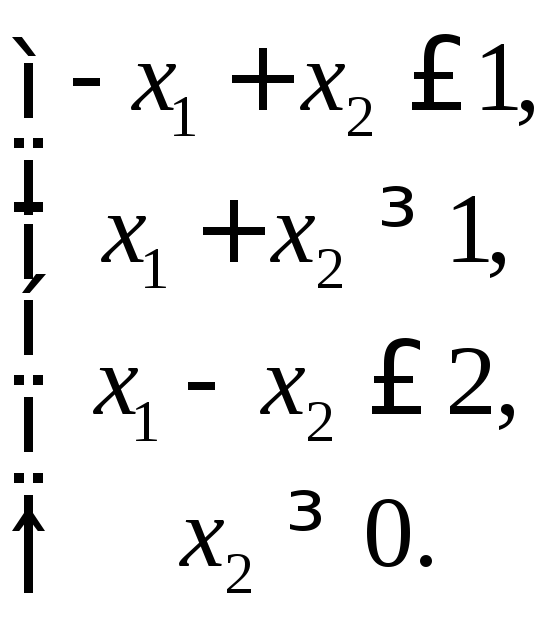
Построим прямые, описываемые соответствующими уравнениями:

-х₁ +х₂= 1 ( прямаяАВ) при х₁= 0х₂= 1 прих₂= 0х₁= -1,

х₁+х₂ = 1 ( прямаяСD) прих₁= 0х₂= 1 прих₂ = 0х₁= 1,

х₁-х₂= 2 ( прямаяЕF) прих₁= 0х₂= -2 прих₂= 0х₁= 2,

х₂= 0 ( прямая - осьх₁).

Теперь найдем область решения для каждого неравенства, используя контрольную точку (0,0).

Для неравенства -х₁+х₂1 получим 01, то есть область его решений расположена ниже прямойАВ.

Для неравенства х₁+х₂1 получим 01, то есть область его решений расположена выше прямойСD.

Для неравенства х₁-х₂2, получим 02, то есть область его решения расположена выше прямойЕF.

Для неравенства х₂0 область решений расположена выше оси Ох₁.

Обобщая, получаем, что областью решения системы неравенств является неограниченная фигура BKLMF (рисунок 5.2).

Рисунок 5.2. – Область решения системы неравенств

Координаты угловых точек в данном случае находятся из рисунка: K(0,1),L(1,0),M(2,0).

В общем случае, координаты угловых точек находятся как решение системы двух уравнений, описывающих соответствующие прямые.

Например, координаты точки Кможно найти, решая систему уравнений

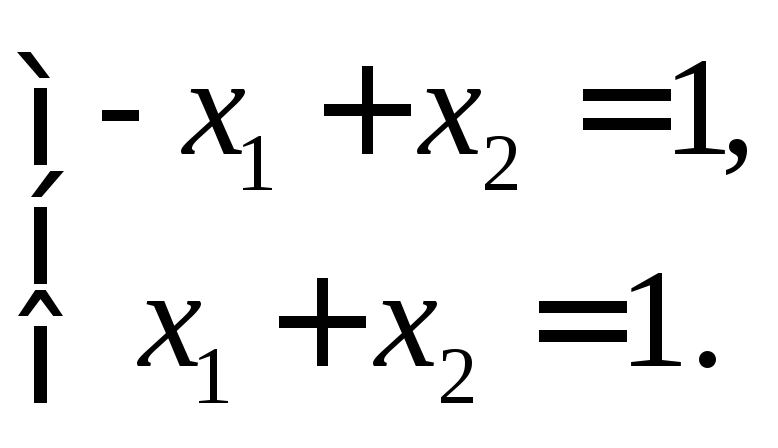
Решая ее, получим х₁=0,х₂=1.