Розв’язування задачі Коші для лінійного др з постійними коефіцієнтами

Нехай треба знайти розв’язок ЛНДР-2 з постійними коефіцієнтами , що задовольняє початковим умовам.

Будемо вважати, що функція та розв’язокразом з їх похідними до другого порядку включно є функціями-оригіналами:. За правилом диференціювання оригіналів з врахуванням початкових умов маємо

.

Застосовуючи до обох частин ДР перетворення Лапласа та користуючись властивістю лінійності перетворення, отримаємо операторне рівняння:

,

.

Знайшовши оригінал для , отримаємо частинний розв’язок ДР, щор задовольняє задані початкові умови.

Аналогічно при ЛНДР-.

Приклад.

Розв’язування систем лінійних др з постійними коефіцієнтами

,

Припустимо, що функції є функціями-оригіналами:.

Застосуємо перетворення Лапласа:

Отримаємо алгебраїчну систему відносно невідомих і.

Приклад. .

Відповідь:

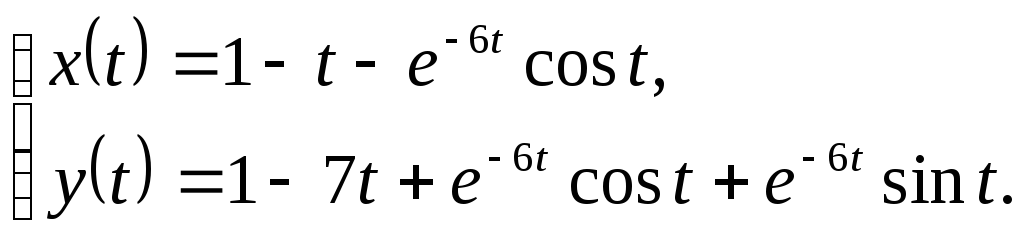
Інтегральні рівняння

Означення. Інтегральним рівнянням називається рівняння, що містить невідому функцію під знаком інтеграла.

Будемо розглядати лише лінійні ІР. Ведемо до розгляду їх основні типи:

1. ІР Фредгольма ІІ роду: ,

2. ІР Фредгольма І роду: ,

3. ІР Вольтерра ІІ роду: ,

4. ІР Фредгольма І роду: .

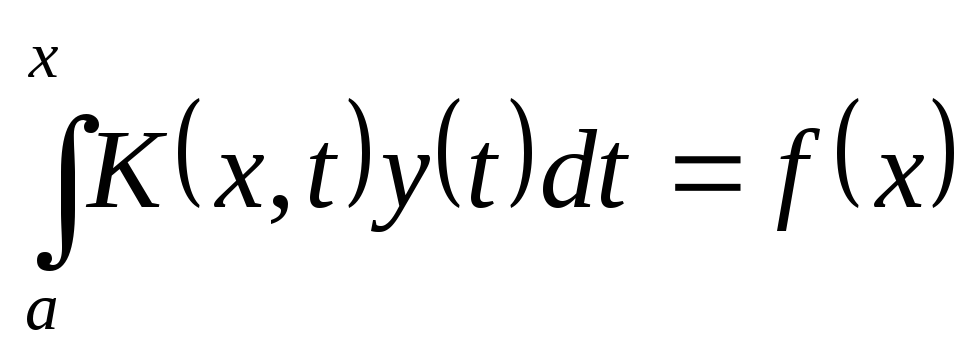Тут - шуканий розв’язок;і- задані функції,- параметр. Функціяназиваєтьсяядром ІР, вільним членом. Якщо , то ІР називаєтьсяоднорідним, якщо -неоднорідним.

Приклади. - неоднорідне Вольтерра ІІ роду

- однорідне Вольтерра ІІ роду

- неоднорідне Вольтерра І роду

- однорідне Фредгольма ІІ роду

- нелінійне

- неоднорідне Фредгольма І роду

- неоднорідне Вольтерра І роду

Інтегральні рівняння Вольтерра

1. Зв’язок між ЛДР та інтегральними рівняннями Вольтерра.

Розв’язок ЛДР з неперервними коефіцієнтамиз початковими умовамиможе бути зведене до розв’язку деякого інтегрального рівняння Вольтерра ІІ роду.

При перетвореннях будемо використовувати формулу

.

Нехай для конкретності маємо ДР-2 ,. Покладемо, тоді враховуючи початкові умови, послідовно знаходимо:

, .

Підставимо в ДР, отримаємо

.

.

Покладемо ,отримаємо.

Існування єдиного розв’язку ІР випливає зі існування та єдності розв’язку задачі Коші для ЛДР з неперервними коефіцієнтами в околі точки .

Справедливе обернене: розв’язуючи ІР, отримаємо єдиний розв’язок ЛДР-2 з початковими умовами.

Приклад. Скласти ІР, що відповідає ДР з початковим умовами.

.

Означення. Ядро називається виродженим, якщо його можна представити у вигляді скінченної суми добутку двох функцій, одна з яких залежить тільки від, а інша тільки від, тобто має вигляд

Тоді ІР матиме вигляд .

Приклад. Розв’язати ІР Вольтерра ІІ роду .

З рівняння випливає, що . Це ЛНДР-1, загальний розв’язок якого. Використовуючи початкову умову.

Приклад.

,

.

З умови , тому , тому,,

.

Приклад. Розв’язати ІР Вольтерра 1-го роду .

Продиференціюємо по праву і ліву частини:

З самого ІР маємо .

2. Розв’язування ір Вольтерра за допомогою резольвенти.

Нехай маємо ІР , де- неперервна при,неперервна при. Розв’язок ІР будемо шукати у вигляді степеневого ряду за степенями:

Підставимо цей ряд в ІР:

Прирівнюючи коефіцієнти при однакових степенях , отримаємо:

,

,

, …

Отримані співвідношення дають спосіб послідовного визначення функцій . При припущеннях щодо функційтаотриманий ряд збігається рівномірно поіприі його сума є єдиний розв’язок ІР. Маємо

,

,

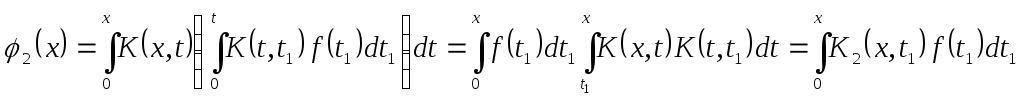де .

Аналогічно .

Функції називаютьсяповторними або ітерованими ядрами, які визначаються за допомогою рекурентних формул

,

Тоді . Функціяназиваєтьсярезольвентою ІР. Даний ряд збігається абсолютно і рівномірно.

Ітеровані ядра (резольвента) не залежать від нижньої межі інтегрування. Резольвента задовольняє наступне функціональне рівняння

За допомогою резольвенти розв’язок ІР запишеться у вигляді

.

Приклад. Знайти резольвенту ІР Вольтерра з ядром .

,

,

,

,

…..

,

.

Приклад. За допомогою резольвенти знайти розв’язок ІР .

,

,

,

…..

.

Тому .