Системи др Основні означення

Означення. Система звичайних ДР ,, розв’язна відносно старших похідних, називаєтьсяканонічною системою. Вона має вигляд

Порядком системи називається число .

Означення. Система звичайних ДР першого порядку виду

,

де - незалежна змінна,- невідомі функції від, називаєтьсянормальною.

Число називаєтьсяпорядком нормальної системи. Дві системи ДР називаються еквівалентними, якщо вони мають одні і ті самі розв’язки.

Приклад. Привести до нормальної системи наступну систему ДР:

Покладемо . Тоді отримаємо,і дана система приведеться до наступної нормальної системи третього порядку:

Означення. Розв’язком системи ДР в називається сукупність довільнихфункцій, визначених та неперервно диференційовних в,якщо вони обертають всі рівняння системи в тотожності, що виконуються для кожного.

Приклад. Показати, що система функцій є розв’язком системи ДР

Означення. Задачею Коші для системи ДР називається задача знаходження розв’язку цієї системи , що задовольняє початковим умовам, де.

Можна навести

теорему (існування та єдності розв’язку задачі Коші). Нехай маємо нормальну систему ДР і нехай функції визначені в деякійвимірній областізмінних. Якщо існує окіл точки, в якому функціїнеперервні і мають обмежені частинні похідні по змінним , то знайдеться інтервал, в якому існує єдиний розв’язок нормальної системи, що задовольняє початкові умови.

Означення. Система диференційовних функцій,, називаєтьсязагальним розв’язком нормальної системи ДР, якщо: 1) при всіх припустимих значеннях система функційобертає всі рівняння системи в тотожності; 2) в області, де виконуються умови теорем Коші, функціїрозв’язують будь-яку задачу Коші.

Означення. Розв’язки, отримані із загального при конкретних значеннях сталих , називаютьсячастинними.

Розглянемо нормальну систему 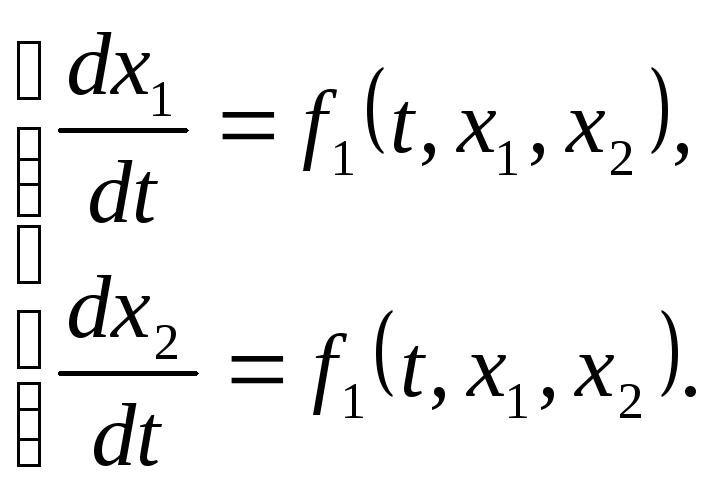Значеннярозглянемо як прямокутні декартові координати точки тривимірного простору. Розв’язокщо приймає призначеннязображує в цьому просторі деяку лінію, що проходить через точку, яка називаєтьсяінтегральною кривою нормальної системи.

Задача Коші має наступну геометричну інтерпретацію: в просторі знайти інтегральну криву, що проходить через точку. Теорема Коші встановлює існування та єдність такої лінії.

Метод виключення

Частинним випадком канонічної системи ДР є одне рівняння -го порядку, розв’язне відносно старшої похідної:.

Введенням нових функцій це рівняння замінюється нормальною системоюрівнянь:

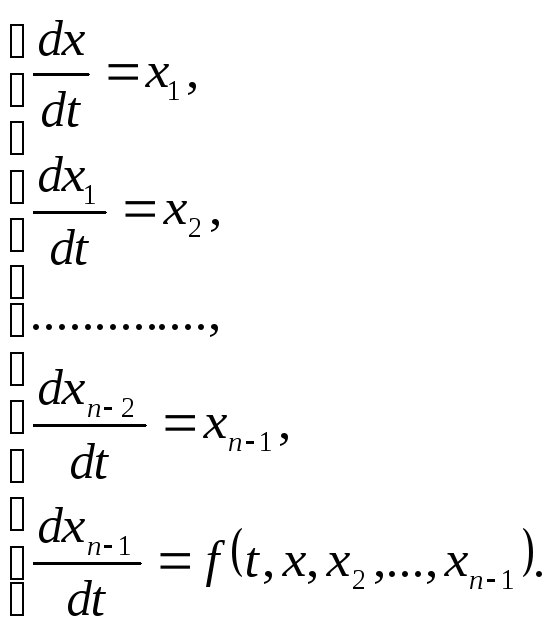
Можна стверджувати і обернене: нормальна система рівнянь першого порядку еквівалентна одному рівнянню-го порядку. На цьому засновано один з методів інтегрування систем ДР – метод виключення.

Проілюструємо його на системі 2-го порядку .

З першого рівняння та підставимо в друге рівняння:

Приклад. Розв’язати задачу Коші для системи .

Відповідь:

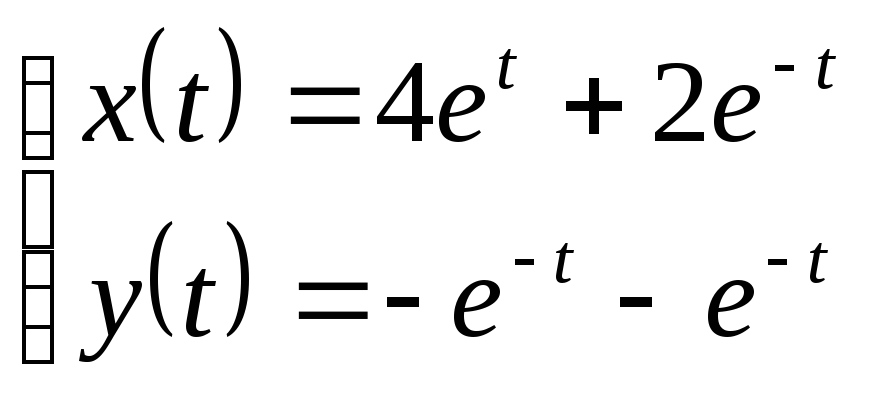
Приклад. Розв’язати систему .

Відповідь:

Зауваження. Не будь-яка система ДР може бути зведена до одного рівняння більш високого порядку. Наприклад,

Метод інтегровних комбінацій

Цей метод полягає в наступному: за допомогою арифметичних операцій (додавання, віднімання, множення, ділення) з рівнянь системи отримують так звані інтегровні комбінації, тобто рівняння системи, які досить просто розв’язуються.

Приклад.

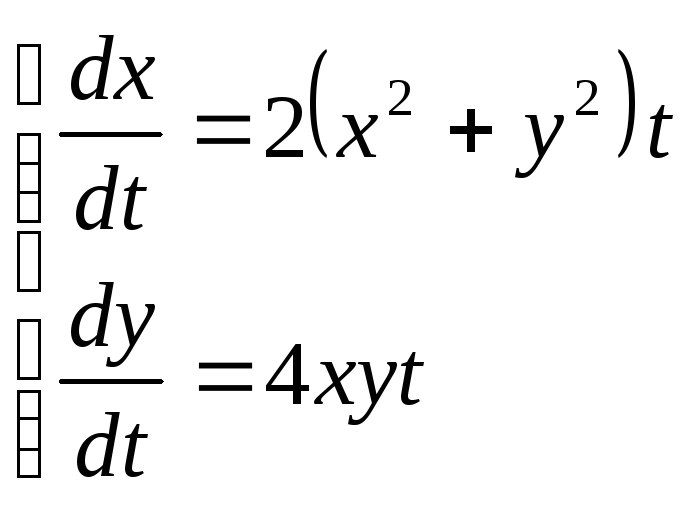
Додамо рівняння системи: .

Віднімемо від першого друге рівняння: .

Розв’яжемо отримані рівності відносно та:

Приклад.

1-2:

Отриману рівність підставимо в 3: .

Підставимо її також у 2: .

Тоді

Приклад. Знайти частинний розв’язок системи що задовольняють початковим умовам.

Запишемо систему у вигляді:

Додамо ці рівняння системи

Оскільки , то друге рівняння системи має вигляд.

Маємо

При маємоі тому частинний розв’язок