Полусумматор

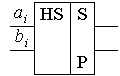
Кроме сумматоров существуют полусумматоры, которые осуществляют сложение двух чисел с формированием сигналов суммы и переноса.

Лекция 12. Одноразрядный комбинационный сумматор

Закон функционирования такого сумматора при сложении трех цифр определяется следующей таблицей.

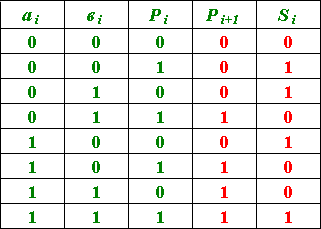
На основании таблицы строятся диаграммы Вейча и получаются минимальные ДНФ функций S_i и P_i+1

Диаграммы Вейча

,

.

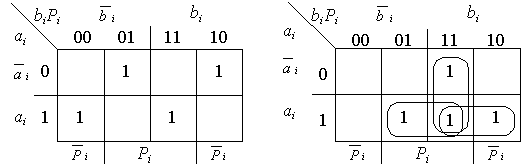
По полученным уравнениям можно построить двухуровневую схему одноразрядного комбинационного сумматора.

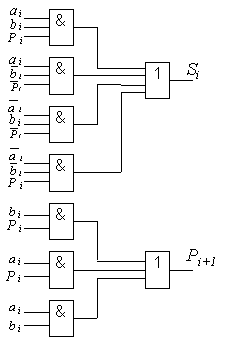
Полученную схему можно упростить, если рассматривать S_i как функцию 4-х переменных S_i=S_i(а_i,в_i,P_i,P_i+1).

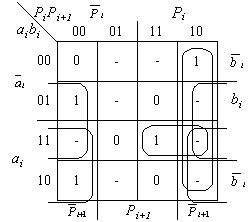
Отсюда имеем:

.

Первая схема, имеющая парафазные входы, обладает большим быстродействием, т.к. число уровней здесь r=2, суммарное число входов у логических элементов равно в₁=25.

Схема с парафазными входами

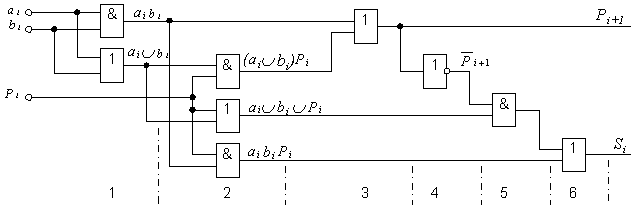
Вторая схема, имеющая однофазные входы, обладает худшим быстродействием, т.к. r=6. Суммарное число входов равно здесь в₂=17, т.е. последняя схема несколько проще.

Схема с однофазными входами

Схема с однофазными входами на элементах И-НЕ и ИЛИ-НЕ имеет вид:

Число уровней r=5, суммарное число входов равно в₃=19, В зависимости от назначения и следует использовать ту или иную схему.

Одноразрядный накапливающий сумматор

Одноразрядным сумматором накапливающего типа является схема, суммирующая поочередно поступающие на ее вход цифры слагаемого и переноса с запоминанием результата суммирования. Для запоминания результата сложения на выходе рассмотренных комбинационных сумматоров можно установить триггеры памяти (триггера R-S и D-типов). Совместно с триггером памяти комбинационный сумматор будет выполнять функции накапливающего сумматора.

Роль накапливающего сумматора может выполнять и счетный триггер со схемой формирования переноса, на счетный вход которого все слагаемые должны подаваться последовательно во времени. Суммирование трех слагаемых будет проходить поэтому за три такта.

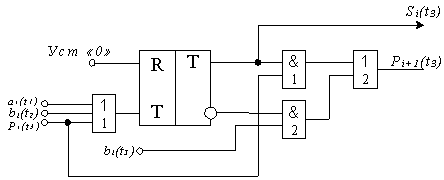
В первый момент времени t₁ через схему ИЛИ1 на вход Т-триггера, который был предварительно установлен в нулевое состояние, поступает цифра a_i и запоминается. После завершения переходных процессов в триггере в момент времени t₂ через схему ИЛИ1 поступает цифра в_i второго слагаемого. При этом Т-триггер реализует функцию . Наконец в следующий момент времени t₃ через схему ИЛИ1 подается цифра переноса из более младшего разряда P_i и триггер реализует функцию: 

, которая совпадает с функцией S_i, полученной ранее по таблице истинности одноразрядного сумматора. Таким образом, по истечении трех тактов в триггере будет находится значение i-ого разряда суммы слагаемых А и В, т.е. S_i.

Сигнал переноса P_i+1 формируется комбинационной схемой, стоящей на выходе триггера. В момент времени t₃, когда триггер еще находится в состоянии f_1, приходит сигнал P_i. На выходе И1 имеем . Если теперь к f₃ добавить через дизъюнкцию a_i×b_i, то получится P_i+1. Непосредственно a_i×b_i получить с помощью конъюнктора нельзя, т.к. они поступают в различные дискретные моменты времени. Поэтому a_i×b_i формируются с помощью элемента И2 реализующего функцию

.

Окончательно, сигнал переноса P_i+1 на выходе ИЛИ2 равен

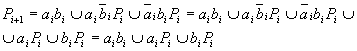
 Этот сигнал совпадает с сигналом, формируемом в комбинационном сумматоре на выходе P_i+1 .

Недостаток рассмотренного сумматора заключается в том, что он имеет малое быстродействие, поскольку в каждом цикле суммирования число срабатываний триггера может равняться четырем (Уст «0», a_i(t₁), b_i(t₂), P_i(t₃)).

Достоинство накапливающего сумматора по сравнению с комбинационным состоит в более простой организации суммирования с накоплением результата, благодаря его способности к запоминанию. Полученная сумма сохраняется в сумматоре и после снятия входных сигналов.

Комбинационно-накапливающий одноразрядный сумматор

Положительные свойства сумматоров накапливающего и комбинационного типов сочетает в себе сумматор комбинационно-накапливающего типа, в котором сигнал переноса вырабатывается комбинационной схемой, а сумма образуется в Т-триггере, на счетный вход которого с помощью другой комбинационной схемы подается результат сложения по модулю два цифр второго слагаемого и переноса.