Диаграммы Вейча

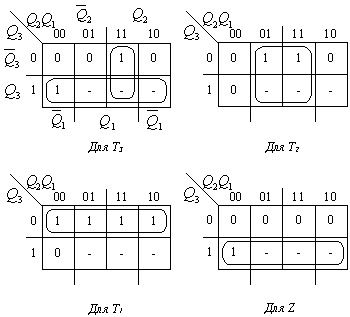
Из диаграмм Вейча получаем следующие выражения для трех функций возбуждения и функции выходов:

Это синхронный пятеричный счетчик.

Синхронный пятеричный счетчик

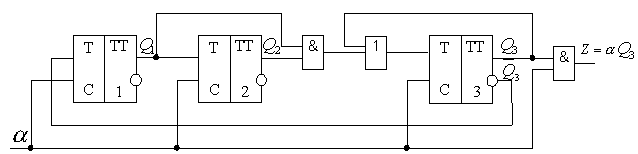
Аналогичным образом может быть синтезирован вычитающий и реверсивный счетчики с различными коэффициентами пересчета. При синтезе реверсивного счетчика появится дополнительный входной сигнал y, управляющий режимом работы счетчика. При сигнале y=0 синтезируем суммирующий счетчик, а при y=1 – вычитающий. Кодированную таблицу переходов строим одну. Студенты синтезируют вычитающий счетчик с коэффициентом пересчета, равным 9, и реверсивный счетчик с коэффициентом пересчета, равным 7 при сложении и вичитании.

Лекция 10. Счетчики на кольцевых сдвигающих регистрах

Эти счетчики строятся на регистрах сдвига, охваченных цепями обратных связей, и применяются в основном при построении схем с небольшим коэффициентом пересчета k.

Простейшим счетчиком такого типа является счетчик, построенный на основе кольцевого сдвигающего регистра, один из разрядов которого предварительно устанавливается в единичное состояние. После каждого счетного импульса осуществляется сдвиг этой единицы на один разряд, и получается переход счетчика в новое состояние. Такой счетчик осуществляет подсчет сигналов по модулю n, т.е. k=n, где n – число разрядов счетчика. Такой счетчик называют еще электронным коммутатором. Основным преимуществом такого счетчика является простота дешифрации его состояний и высокое быстродействие. Недостаток заключается в том, что при больших значениях k требуется большее число триггеров. Эти счетчики обычно строятся на триггерах D, RS и JK типов. Построим схему такого счетчика на синхронных двухступенчатых RS триггерах при k=n=5.

Счетчик на кольцевых сдвигающих регистрах

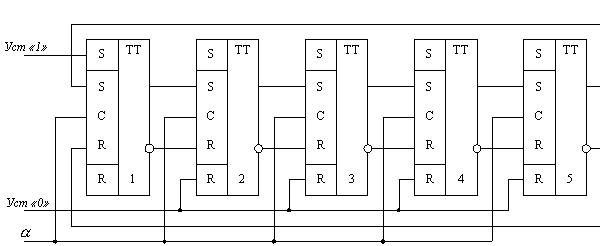
Такой счетчик имеет 5 состояний:

10000 – исходное состояние, затем: 01000, 00100, 00010, 00001,

10000 – вернулись в исходное состояние

Кодовое кольцо.

Если в приведенной схеме счетчика на кольцевом регистре организовать одну перекрестную связь, т.е. прямой выход последнего триггера соединить со входом R первого триггера, а обратный выход – со входом S, то получится счетчик на регистре с перекрестными связями или счетчик Джонсона. Такой счетчик будет иметь число состояний в два раза больше, чем число разрядов, т.е. k=2n. В нашем примере это состояния: 10000, 11000, 11100, 11110, 11111, 01111, 00111, 00011, 00001, 00000, 10000 и т.д. Т.е. пятиразрядный счетчик имеет коэффициент пересчета, равный десяти. Путем исключения из схемы одного «избыточного» состояния, за счет введения элемента И, можно сделать счетчик Джонсона и с нечетным коэффициентом пересчета k=2n-1. Например, счетчик Джонсона с k=9 на D-триггерах имеет вид:

Счетчик Джонсона

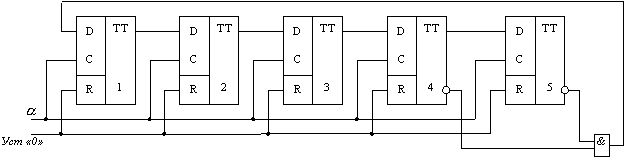
00000 – исходное состояние, затем 10000, 1100, 11100, 11110, 01111, 00111, 00011, 00001, 00000 – вернулись в исходное состояние, состояние 11111 исключено

Полиномиальные счетчики

Полиномиальные счётчики строятся на основе n-разрядного регистра сдвига с линейными обратными связями (с сумматорами по модулю два в цепи обратной связи).

В качестве примера рассмотрим схему счётчика при n = 4:

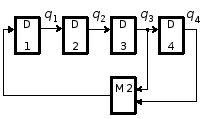
Последовательность состояний регистра сдвига представлена на рисунке (состояние 0 0 0 0 запрещено).

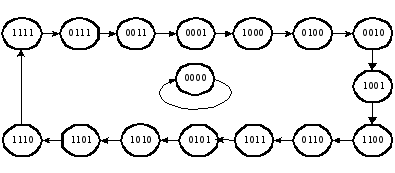
Работа схемы описывается с помощью квадратной матрицы С, связывающей данное и последующеесостояния. Для нее состояния триггеров q₁, q₂, q₃ и q₄ в момент времени (t+1) определятся следующим образом:

или в матричной форме

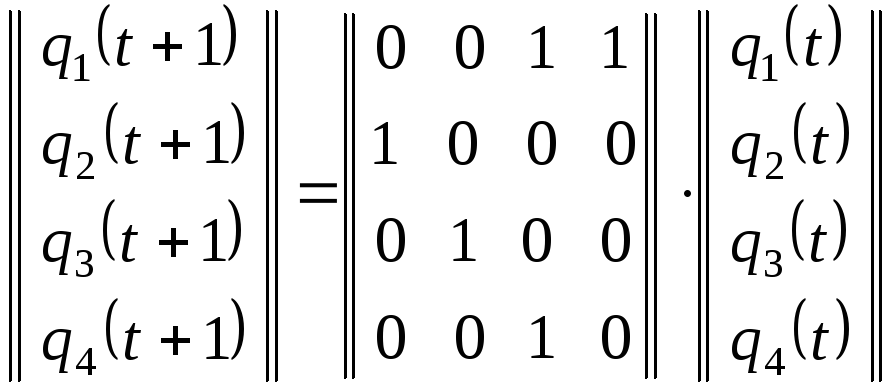
или ,

где

_.

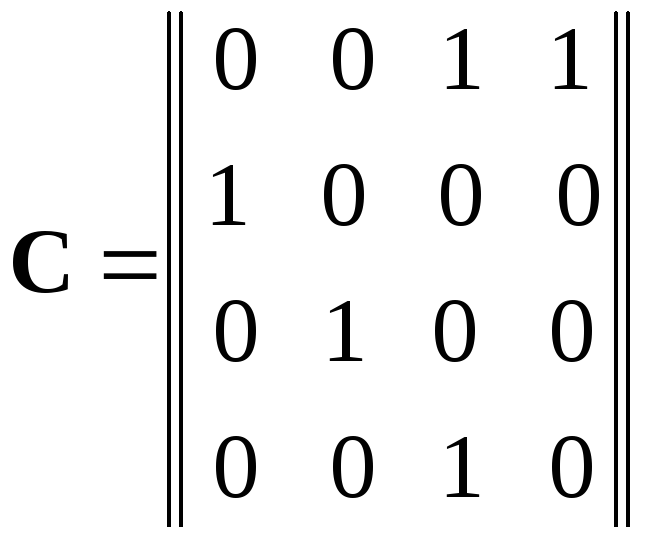Первая строка в матрице C определяется видом обратной связи регистра сдвига, остальные единичные элементы матрицы определяют операцию сдвига содержимого регистра.

Периодические свойства последовательностей на выходах счетчика определяются характеристическим многочленом , который является определителем матрицы (Е – единичная матрица).

Если многочлен неприводим и примитивен, то счетчик будет формировать последовательность максимальной длины или М- последовательность. Для данного примера характеристический многочленj (х) неприводим, примитивен и имеет следующий вид: =x⁴ x 1.

Вероятности появления символа 1 и символа 0 для М-последовательности определяются следующим образом:

, .

Известен оригинальный метод построения счетчика на регистре с многошаговым (s-шаговым) сдвигом за один рабочий такт (). Запишем следующие соотношения:

,и т.д.

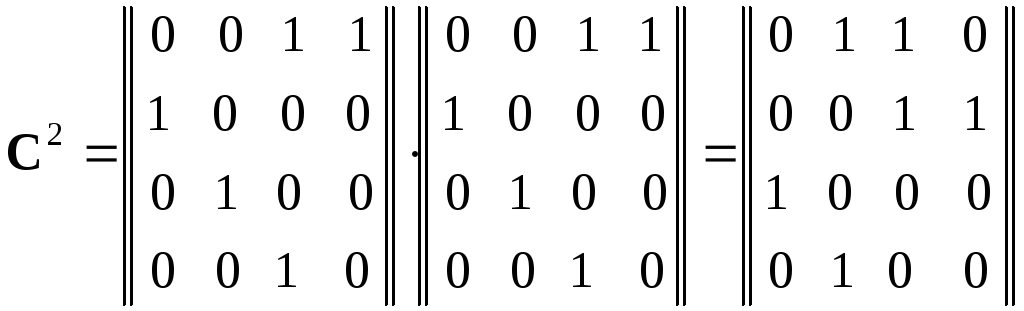
Пусть s = 2. Тогда матрица будет имеет вид:

.