Раздел I. Введение. Общие сведения о цифровых автоматах Лекция 1. Основные понятия и определения.

В ЭВМ обрабатывается числовая информация, представленная в двоичной системе счисления, т.е. информация представлена в виде комбинации нулей и единиц. Поэтому работу любой схемы ЭВМ можно рассматривать как функциональный преобразователь с большим числом входов и выходов. При этом поступление на входы некоторой последовательности входных сигналов, состоящих из нулей и единиц, вызывает появление на выходах вполне определенной последовательности выходных сигналов, также состоящей из нулей и единиц.

Все схемы ЭВМ можно разделить на два больших класса:

1. Класс логических или комбинационных схем (КС).

2. Класс конечных автоматов.

В логических (комбинационных) схемах значение выходных сигналов в момент времени t однозначно определяется значениями входных сигналов в момент времени t₁ t.

Выходные сигналы в схемах второго класса определяются не только значениями входных сигналов в данный момент времени, но и состояниями схемы, которые в свою очередь зависят от значении сигналов, поданных на её входы во все предшествующие моменты времени. Эти схемы обязательно содержат в своем составе элементы памяти, в качестве которых используется триггера различных типов.

Технические вопросы синтеза комбинационных схем решаются с помощью аппарата математической логики. При этом используется самая простая часть математической логики, а именно, алгебра логики или Булева алгебра. Основным понятием в алгебре логики, на котором основывается её приложение к синтезу КС, является понятие Булевой или переключательной функции (ПФ).

Переключательной или Булевой функцией называется функция f(x1, x2, …, xn), способная принимать так же как и её аргументы x1, x2, …, xn только два значения 0 или 1.

Таким образом, аргументы и функции от них могут быть либо истинными, либо ложными. Ввиду того, что аргументы ПФ могут принимать только два значения, область определения любой ПФ конечна. Поэтому любая ПФ может быть задана таблицей ее значений в зависимости от значений ее аргументов. Эту таблицу называют таблицей истинности ПФ. Совокупность значений аргументов принято называть набором.

Свойства переключательных функций.

1. Любая ПФ n аргументов определена на 2ⁿ наборов.

2. Число различных ПФ n аргументов конечно и равно .

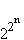Мы будим использовать аппарат алгебры логики к синтезу схем ЭВМ. Это использование основано на следующем: будем отождествлять значение ПФ с выходными сигналами КС, а ее аргументы – с входными сигналами. Тогда ПФ будет описывать процесс преобразования КС входных сигналов в выходные и аппарат Булевой алгебры можно применять при синтезе таких схем. Под синтезом КС будем понимать определение таких способов соединения нескольких простейших схем, называемых логическими элементами, при которых построеные схемы реализуют заданный алгоритм преобразования сигналов при заданном критерии качества. В качестве критерии оценки качества технической реализации заданного алгоритма обычно используют критерий сложности или быстродействия схем.

Общий вид КС можно представить следующим образом:

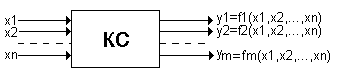
Схема имеет n входов и m выходов и следовательно реализуют m ПФ от n аргументов. Любая сколь угодно сложная КС строится из более простых схем, называемых логическими элементами.

Логическим элементом называется электронная схема, реализующая элементарную ПФ и имеющая количество входов, равное числу аргументов ПФ и только один выход.

В ЭВМ в основном используются логические элементы с одним или двумя входами, реализующие ПФ одного или двух аргументов. Поэтому задача синтеза КС заключается в том, чтобы из логических элементов построить любую сколь угодно сложную схему, реализующую заданный набор ПФ. Математически в алгебре логики этой задачи соответствует задача представления любой сложной ПФ через элементарные ПФ. При составлении сложных КС из логических элементов используют два приема:

1. Последовательное соединение элементов.

2. Перестановка входов элементов.

Пусть имеется два логических элемента, реализующие ПФ f1(x1, x2) и f2(у1, у2). При последовательном соединении этих элементов получим схему, реализующую функцию уже трех аргументов:

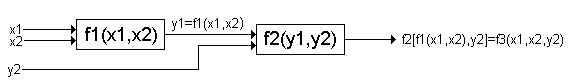
Эта схема реализует функцию f3(x1,x2, y2), получаемую в результате постановки вместо аргумента y1 функции f2 (y1,y2) значение функции f1(x1,x2). Подстановка в функцию вместо ее аргументов других функций называется суперпозицией.

Таким образом, последовательному соединению логических элементов соответствует математическая операция суперпозиция.

Изменим порядок подключения входов элементов.

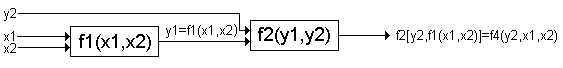
В этом случае схема реализует функцию f4(y2,x1,x2), которая в общем случае отличается от функции f3(x1,x2, y2). В математическом плане мы заменили одни аргументы ПФ другими.

Замена одних аргументов функции другими или изменение порядка записи аргументов называется подстановкой аргументов.

Таким образом, перестановка входов логических элементов соответствует математической операции подстановки аргументов. В Булевой алгебре доказывается, что из ПФ одного или двух переменных можно с помощью операций суперпозиции и подстановки получить все ПФ от большего числа аргументов. Для нас это означает, что из логических одно или двухвходовых элементов можно построить любую сколь угодно сложную КС.

Рассмотрим ПФ от разного числа аргументов.

Переключательные функции одного аргумента.

Существует четыре различных ПФ одного аргумента, таблица истинности которых имеет следующий вид:

Х	f0(x)	f1(x)	f2(x)	f3(x)
0	0	0	1	1
1	0	1	0	1

Функция f₀(x) называется константой нуля и обозначается f₀(x)=0 при любом x.

Аналогично функция f₃(x) и называется константа единицы т.е. f₃(x)=1.

Функция f₁(x) повторяет значение аргумента x и следовательно f₁(x)=x.

Функция f₂(x) принимает значение противоположное значению аргумента x. Эту функцию называют отрицанием (инверсией) переменной x и вводят для нее специальное обозначение f₂(x)=. Черта стоящая над аргументом имеет смысл определенного функционального преобразования и называется знаком отрицания.

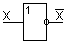
Логический элемент, реализующий функцию отрицания, называют элементом НЕ или инвертором и по ГОСТу обозначают следующим образом:

Переключательные функции двух аргументов.

Для двух аргументов существует четыре набора значений переменных и шестнадцать различных ПФ.

X1	X2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

В шестнадцать ПФ входят также функции, которые зависят от меньшего числа аргументов. Таких функций в таблице истинности шесть:

f₀(x1,x2)=0 – функция константа нуля.

F₁₅(x1,x2)=1 – функция константа единицы.

F₃(x1,x2)=х1,

F₅(x1,x2)=х2,

F₁₂(x1,x2)=,

F₁₀(x1,x2)=.

Рассмотрим оставшиеся десять ПФ от двух аргументов.

Функция f₁(x1,x2) называется логическое произведение или конъюнкция и обозначается: f(x1,x2)=х1*х2=х1^х2=х1&х2.

Таблица истинности этой функции совпадает с таблицей умножения двух одноразрядных двоичных чисел т.е. f₁(x1,x2)=1 тогда, когда аргументы равны между собой и равны единице, в остальных случаях функция равна нулю. Логический элемент, реализующий эту функцию, называют элементом И или конъюнктором. Обозначение конъюнктора на функциональных схемах:

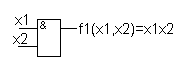
Конъюнкция легко обобщается на случае n аргументов, когда реализуется функция вида: f(x1,x2,…,xn)=x1*x2*…*xn. Функция конъюнкция n аргументов равна единице тогда, когда все аргументы равны единицы.

Функция f7(x1,x2) – называется дизъюнкцией х1 или х2 и обозначается f7(x1,x2)=x1vx2.

Дизъюнкция реализуется элементом, который называется элементом ИЛИ или дизъюнктором.

Сигнал на выходе дизъюнктора принимает нулевое значение только в том случае, если ни один из входных сигналов не имеет в данный момент времени единичное значение.

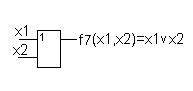
Функция f9(x1,x2)=x1~x2 – равна единице тогда, когда оба аргумента равны между собой. Это функция носит название логической равнозначности.

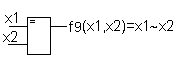
Функция f6(x1,x2)=x1x2 – логическая неравнозначность или сумма по модулю 2. эта функция принимает единичное значение тогда, когда х1≠х2. Второе название этой функции объясняется тем, что таблица истинности f6 совпадает с таблицей сложения двух одноразрядных двоичных чисел по модулю 2, т.е. 0+0=0, 1+0=1, 0+1=1, 1+1=0. Обобщим эту функцию на случай n аргументов. Такая функция принимает единичное значение тогда, когда число аргументов равных единице нечетно и равна нулю если число аргументов четно.

Функции f11(x1,x2)= и f13(x1,x2)=называются импликациями и читаются: если х2, то х1 дляf11, или если х1, то х2 для f13.

Функция f11 принимает нулевое значение только тогда, когда х2=1, х1=0.

Функция f2(x1,x2)=x1x2 – читается: не верно, что если х1, то х2 и является инверсией функции импликации f13.

.

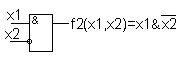Функция f13:

.

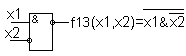Функция f14(x1x2)=x1/x2=называется штрихом Шеффера и является отрицанием функции конъюнкции. Элемент, реализирующий эту функцию, называется элемент И-НЕ и обозначается:

.

f8(x1x2)=x1↓x2=. Функция f8 – называется стрелкой Пирса и является отрицанием от дизъюнкции. Элемент, реализующий эту функцию, называется элемент ИЛИ-НЕ и обозначается:

Две последних функции играют очень важную роль в вычислительной технике, поскольку все остальные функции могут быть выражены через каждую из них.

Система ПФ {f1, f2,,…,fm}, из которых с помощью операций суперпозиции и подстановки можно получить любую сколь угодно сложную ПФ, называется функционально полной системой (ФПС) ПФ. Такие системы ПФ называют базисом.

Приведем примеры некоторых базисов:

1. f=x1/x2

2. f=x1↓x2

Первые два базиса называются универсальными. Кроме универсального базиса существует булев базис:

3. f1=x1vx2

f2=x1&x2

f3=

4. f1=x1x2

f2=x1&x2

f3=1 – базис Жигалкина

Возникает вопрос какие ПФ представляют наибольший практический интерес?

Оказывается, что наиболее удобный для решения задач синтеза схем ЭВМ является ФПС ПФ, содержащая операции конъюнкция, дизъюнкция и отрицание, т.е. булев базис. Этот набор ПФ обладает замечательным свойством: может построить любую КС так, что она будет содержать наименьшее количество элементов, в крайнем случае, равное. Поэтому эта система называется основной функционально полной системой ПФ.

Логические элементы.

Среди систем элементов, выпускаемых промышленностью, наибольшее распространение получили логические элементы, реализующие операции: И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ, а так же элементы булевого базиса.

В эту систему элементов входят как элементы универсального базиса: И-НЕ, ИЛИ-НЕ, так и комбинации операций булевого базиса: И-ИЛИ-НЕ.

Логические элементы характеризуются следующими параметрами:

1. коэффициентом объединения;

2. коэффициентом разветвления.

1. Коэффициент объединения. Из-за взаимных наводок в цепях передачи сигналов возникают помехи, которые суммируются при объединении нескольких цепей на одном элементе. Поэтому для исключения возможности появления недопустимо больших помех, налагаются ограничения на предельное число входных сигналов в одном элементе. Это число входов и называется коэффициентом объединения J.

Если требуемое число входов элементов больше значения J, то производится так называемое разделение входов с помощью дополнительных элементов.

Покажем процедуру разделения входов на примерах:

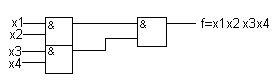
1. Пусть необходимо реализовать в булевом базисе функцию от четырёх аргументов f=x1x2x3x4 при J=2.

2. Пусть необходимо реализовать функцию f=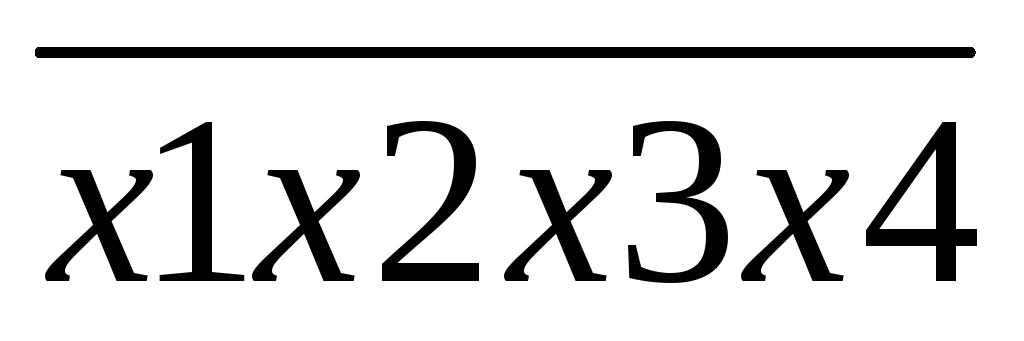в базисе И-НЕ приJ=2.

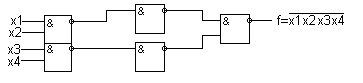
Разделение входов всегда сопровождается уменьшением быстродействия т.к. увеличивается суммарное задержка сигналов.

2. Коэффициент разветвления обозначается F. Всякий реальный элемент обладает конечной нагрузочной способностью, не позволяющей подсоединить выход одного элемента к неограниченному числу входов других элементов. Нарушение нагрузочной способности приводит к искажению сигналов в схеме. Нагрузочная способность элемента характеризуется коэффициентом разветвления F, т.е. наибольшим количеством входов других элементов, которые можно подсоединить к выходу данного элемента. Если число входов элементов, подключаемых к выходу данного элемента больше F, то принимаются меры к разгрузке данного элемента. Разгрузка может выполнятся двумя способами:

1. Дублированием выходного сигнала.

2. Дублированием элемента.

Покажем, как производится разгрузка элементов на примерах:

Пусть F=4 и к выходу некоторого элемента необходимо подключить семь входов других элементов. Тогда для дублирования сигнала можно использовать два инвертора.

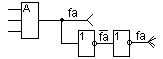
Пусть элемент имеет два выхода прямой и инверсный:

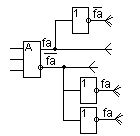
Недостаток этого метода заключается в увеличении задержки сигнала в схеме. От этого недостатка свободен способ разгрузки за счет дублирования элемента.