Счетчик на синхронных т-триггерах

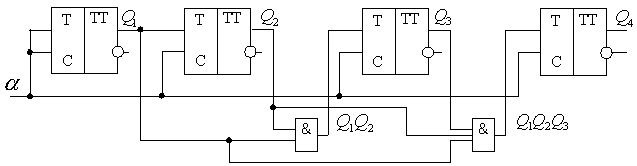
В таком счетчике изменение состояния всех триггеров происходит одновременно. Частота работы такого счетчика определяется из следующего выражения . Здесь Δt - время задержки сигнала коньюнктором. Разрядность счетчика с параллельным переносом ограничивается возможностями логических элементов: коэффициентом разветвления и коэффициентом объединения. Поэтому иногда бывает целесообразно строить менее быстродействующую схему, но с использованием только двухвходовых логических элементов. При синтезе такого счетчика достаточно переписать функции возбуждения, полученные ранее, в виде T₁=a; T₂=Q₁T₁; T₃=T₂Q₂; T₄=T₃Q₃; … T_n=T_n-1Q_n-1 или T₁=1; T₂=Q₁; T₃=T₂Q₂; T₄=T₃Q₃;

Счетчик построенный по этим уравнениям, называется счетчик со сквозным переносом.

Счетчик со сквозным переносом

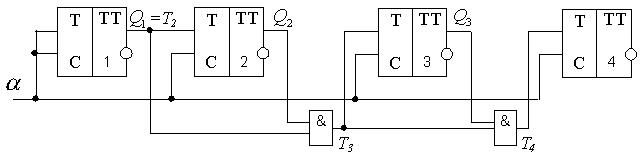
Максимальная частота работы такого счетчика равна

Существует еще один тип счетчиков с так называемым групповым переносом. Эти счетчики занимают по быстродействию и количеству оборудования промежуточное место между счетчиками с одновременным и сквозным переносом и используются в случае, когда число разрядов велико. В таких случаях счетчик разбивается на группы разрядов, в пределах каждой из которых строят цепи одновременного переноса. Перенос между группами реализуется обычно методом сквозного переноса. Рассмотрим процесс построения такого счетчика. Пусть n разрядов счетчика делятся на группы по k разрядов. Введем обозначения T_{l гр} – перенос на вход l-ой группы ;

T_{l гр j} - перенос на вход j-го разряда в l-ой группы . Примем для простотыn=9, k=3. Тогда формулы, полученные ранее для функций возбуждения можно представить в виде:

T_{1 гр}=T₁=1;

T_{2 гр}=T_{l гр}(Q₃Q₂Q₁)=Q₃Q₂Q₁=T₄;

T_{3 гр}=T_{2 гр}(Q₆Q₅Q₄)=T₇;

T_{4 гр}=T_{3 гр}(Q₉Q₈Q₇)=T₁₀;

Из этих формул видно, что между группами разрядов можно организовать цепи сквозного переноса, а внутри каждой группы одновременный перенос.

Организация цепей сквозного переноса

Т.е. в этой схеме каждый из трехразрядных счетчиков с одновременным переносом может быть выполнен не только на Т-триггерах, но и на других типах триггеров, например на JK-триггерах со сложной входной логикой. Здесь группы входов по J и K связаны внутри каждой из групп по И, т.е.

Счетчики с коэффициентом пересчета,    не равным целой степени двух k¹2ⁿ

Рассмотренные схемы n-разрядных счетчиков имеют коэффициент пересчета k, равный целой степени двух (k=2ⁿ). Для многих устройств ЭВМ необходимы счетчики с k¹2ⁿ. Такие счетчики называют еще пересчетными схемами. Эти счетчики получают, вводя в схему обратные связи, управляющие переходом двоичного счетчика из состояния, соответствующего числу k-1, в нулевое состояние.

Синтезируем счетчик с коэффициентом пересчета равным пяти (на Т-триггерах). Такой счетчик имеет пять состояний (от 0 до 4). В исходном состоянии счетчик находится в нуле. После поступления на его вход пяти импульсов он снова должен оказаться в нулевом состоянии. Количество триггеров определяется согласно формуле , где k=5 – число состояний. Отсюда . Выходной сигнал Z=1 должен формироваться на каждый пятый входной сигнал. В результате получается кодированная таблица переходов, выходов и сигналов возбуждения.

Таблица

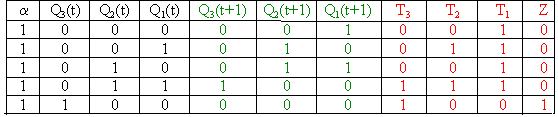
При a=1 строим следующие диаграммы Вейча