Временная диаграмма

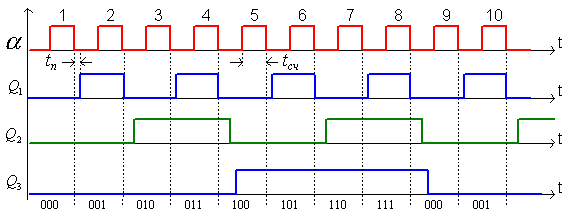
Максимальная частота работ этого счетчика определяется максимально допустимой частотой переключения его младшего разряда.

Для двухступенчатых триггеров частота счетных импульсов определяется из условия , где t_сч – длительность счетных импульсов, t_n – время переключения второй ступени триггера.

Поскольку опрос состояния всех разрядов может происходить только в паузе между сигналами счета, т.е. после того, как завершился переходной процесс, связанный с переключением всех триггеров, имеем . Здесь n- разрядность счетчика, t_опр – длительность сигнала опроса, nt_n – время полного переключения n разрядов счетчика.

Вычитающий счетчик. Реверсивный счетчик

Вычитающий счетчик также может быть построен из последовательно соединенных Т-триггеров. На вход младшего разряда счетчика поступают сигналы счета, а входы последующих разрядов соединены с обратными выходами предшествующих триггеров. В результате получается асинхронный вычитающий счетчик с последовательным переносом.

Асинхронный вычитающий счетчик

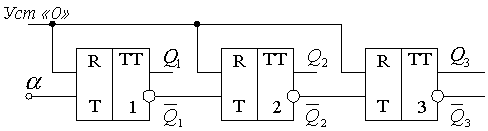
Для построения реверсивного счетчика необходимо объединить схемы суммирующего и вычитающего счетчиков. Схема асинхронного реверсивного счетчика с последовательным переносом имеет вид

Асинхронный реверсивный счетчик

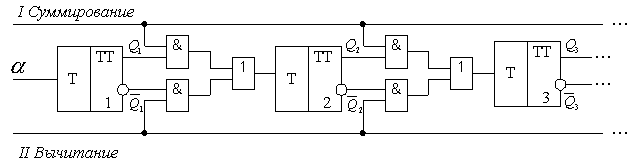
Здесь при наличии единичного сигнала на управляющей шине I счетчик работает как суммирующий, а при наличии единичного сигнала на управляющей шине II – как вычитающий. Обычно счетчики имеют цепи установки в нулевое и единичное состояния. Нарисуем схему асинхронного реверсивного счетчика на синхронных JK – триггерах, имеющих асинхронные установочные входы R и S (инверсные).

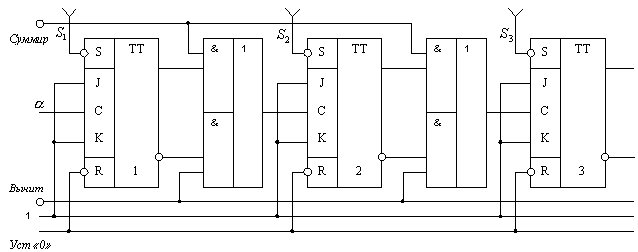
Счетчики с последовательным переносом наиболее просты, но имеют невысокое быстродействие. Для увеличения быстродействие схему формирования сигнала переноса усложняют.

Лекция 9. Счетчики с одновременным, сквозным и групповым переносом

Для ускорения процесса счета в счетчике необходимо, чтобы изменения состояний отдельных разрядов происходило не последовательно, а непосредственно вслед за приходом очередного сигнала счета. Как правило, такие счетчики строят на синхронных двухступенчатых Т-триггерах. При этом счетные сигналы подаются по шине a на синхронизирующие входы триггеров всех разрядов одновременно. Сигнал же на входе Т каждого триггера формируется логической схемой в зависимости от состояний всех триггеров счетчика. Синтез такого счетчика можно провести на основании кодированной таблицы переходов трехразрядного счетчика и таблицы функций возбуждения.

Таблица

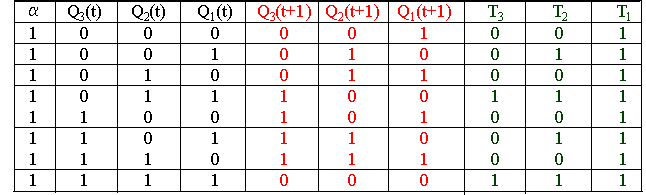
На основании этой таблицы построим диаграммы Вейча для сигналов возбуждения триггеров, рассматривая их как функции состояний триггеров Q₁(t), Q₂(t), Q₃(t). При a=1. Имеем:

Диаграммы Вейча

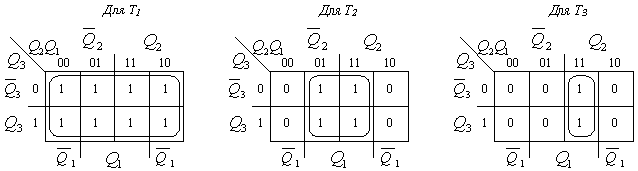
Из диаграмм получаем следующие выражения для сигналов возбуждения триггеров T₁=a; T₂=Q₁a; T₃= Q₁Q₂a; или T₁=1; T₂=Q₁; T₃= Q₁Q₂;

Если бы мы синтезировали n-разрядный счетчик, то получили бы следующие выражения для сигналов возбуждения триггеров:

T₁=a; T₂=Q₁a; T₃=Q₁Q₂a; T₄=Q₁Q₂Q₃a; … T_n=Q₁Q₂Q₃…Q_n-1a

Счетчик, построенный в соответствии с этими уравнениями носит название счетчика с одновременным или параллельным переносом.

Т.к. во всех функциях возбуждения присутствует входной сигнал a, то такой счетчик целесообразно строить на синхронных Т-триггерах, подавая счетные сигналы на входы синхронизации всех триггеров. В результате получаем следующую схему: