2.7. Индуктивный элемент в цепи синусоидального тока.

Пусть к цепи рис. 2.9 подведено синусоидальное напряжение

или в комплексной форме

.

Как показано в разделе 2.2 напряжение в цепи с индуктивностью пропорционально скорости изменения тока, т.е. , т.е.

или

.

(2.26)

После интегрирования 2.26 получим

или

(2.27)

т.е. ток в идеальной индуктивной цепи, так же как и напряжение, изменяется по закону синуса и отстает по фазе от напряжения на одну четверть периода. Амплитуда тока связана с амплитудой напряжения соотношением

.

(2.28)

Поделив обе части 2.28 на получим

,

(2.29)

L – имеет размерность сопротивления, обозначается X_Lи называется индуктивным реактивным сопротивлением, т.к. , то

.

(2.30)

Нетрудно видеть, что индуктивное сопротивление растет с увеличением частоты.

Поделив комплекс напряжения на комплекс тока получим

,

(2.31)

jX_L– называется комплексом индуктивного сопротивления, он может принимать только положительные значения.

Выражения 2.28, 2.29 и 2.31 представляют собой закон Ома для идеальной индуктивной цепи соответственно для амплитудных, действующих значений напряжения и тока, а также в комплексной форме.

Всоответствии с комплексами напряжения и тока, векторная диаграмма идеальной индуктивной цепи построена на рис. 2.10.

Мгновенное значение мощности q_Lэтой цепи равно произведению мгновенных значений тока и напряжения:

.

После преобразования получим

,

(2.32)

т.е. мгновенная мощность в идеальной индуктивной цепи также как ток и напряжение есть синусоидальная величина, и изменяется с удвоенной частотой по отношению к току и напряжению. Волновые диаграммы напряжения, тока и мгновенной мощности, приведенные на рис. 2.11, показывают, что мгновенная мощность положительна только в четные четверти периода, когда ток и напряжение имеют одинаковое направление. В эти промежутки времени энергия от источника поступает в приемник, где накапливается в магнитном поле.

,

(2.33)

а т.к. , то

,

(2.34)

В нечетные периоды, когда напряжение и ток имеют противоположные направления, мгновенная мощность отрицательна. Это означает, что энергия, накопленная в магнитном поле приемника, возвращается источнику. Таким образом, при работе идеального индуктивного приемника энергия циркулирует между источником и магнитным полем приемника, а преобразования ее в другие виды не происходит, поэтому средняя мощность за период равна нулю. Такая цепь называется индуктивной реактивной.

2.8. Емкостный элемент в цепи синусоидального тока.

Пусть к цепи рис. 2.12 действует синусоидальное напряжение

или в комплексной форме

.

Как показано в разделе 2.2., ток в цепи с емкостью пропорционален скорости изменения напряжения, т.е. , т.е.

.

(2.35)

После дифференцирования 2.35 получаем:

,

(2.36)

или в комплексной форме

.

(2.37)

Как видно из 2.36 ток в идеальной емкостной цепи так же, как и напряжение изменяется по синусоидальному закону и опережает напряжение по фазе на одну четверть периода. Амплитуда тока связана с амплитудой напряжения соотношением:

.

(2.38)

Поделив обе части 2.38 на получим:

,

(2.39)

– имеет размерность сопротивления, обозначается Х_Си называется емкостным реактивным сопротивлением.

.

(2.40)

Из 2.40 видно, что емкостное сопротивление уменьшается с увеличением частоты.

Поделив комплекс напряжения на комплекс тока, получим

,

(2.41)

– jXc – называется комплексом емкостного сопротивления, он может принимать только отрицательные значения.

Выражения 2.38, 2.39, 2.41 представляют собой закон Ома для идеальной емкостной цепи соответственно для амплитудных и действующих значений напряжения и тока, а также в комплексной форме.

Всоответствии с комплексами напряжения и тока векторная диаграмма идеальной емкостной цепи построена на рис. 2.13.

Мгновенное значение мощности q_Cэтой цепи равно произведению мгновенных значений напряжения и тока

, т.е.

(2.42)

мгновенная мощность в емкостной цепи также как ток и напряжение есть синусоидальная величина, изменяющаяся с удвоенной частотой по отношению к току и напряжению. Волновые диаграммы напряжения, тока и мощности, приведенные на рис. 2.14, показывают, что мгновенная мощность положительна только в нечетные четверти периода, когда ток и напряжение имеют одинаковое направление. В эти промежутки времени энергия от источника поступает в приемник, где накапливается в электрическом поле.

,

(2.43)

а т.к. i=C, то

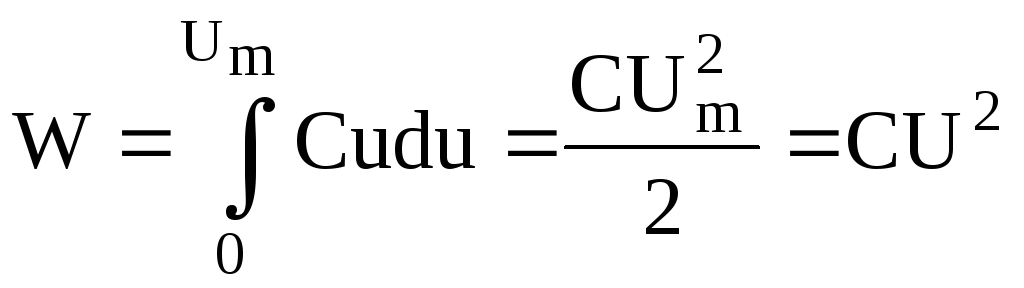. (2.44)

В четные четверти периода, когда напряжение и ток имеют противоположные направления, мгновенная мощность отрицательна. Это означает, что энергия, накопленная в электрическом поле приемника, возвращается к источнику. Таким образом, при работе идеального емкостного приемника энергия циркулирует между источником и электрическим полем приемника, а преобразования ее в другие виды не происходит, поэтому средняя мощность за период равна нулю. Такая цепь называется емкостной реактивной.
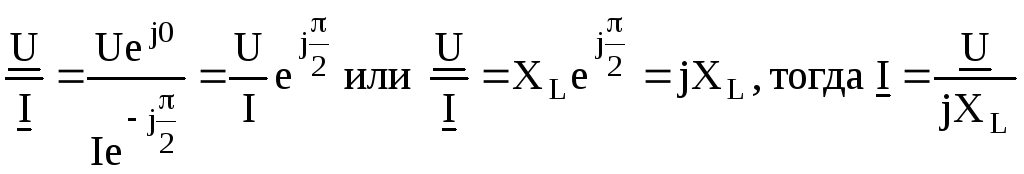