книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

аксиома памяти, в соответствии с которой текущие значения параметров состояния среды несущественно зависят от их значений в отдаленном прошлом.

Следствием постулата макроскопической определимости является принципиальная возможность изучения в достаточно малой окрестности свойств деформируемого твердого тела на образцах конечных размеров с однородным, не зависящим от координат, напряженным и деформированным состоянием. Под достаточно малой окрестностью внутри шара с достаточно малым радиусом, как это определено ранее (п. 1.2), здесь понимается окрестность с малым объемом ΔΩ, в котором в каждый момент времени напряженное и деформированное состояния, непрерывно изменяющиеся во времени, можно считать однородными. По отношению к малому объему ΔΩ в окрестности материальной частицы m деформируемого тела под M образцом понимается любое тело необходимых конечных размеров, вещество которого и его термомеханическое состояние в начальный момент времени t0 одинаковы с веществом и его термомеханическим состоянием во всем объеме ΔΩ в начальный момент времени t0. При этом должны соблюдаться следующие условия:

1)однородность напряженного и деформированного состояний M-образца по его объему в любой момент времени;

2)осуществимость любого процесса деформации или нагружения во времени;

3)осуществимость проникающего действия потоков (тепловых, массовых) через границу M-образца и однородность распределения в нем в любой момент времени параметров, связанных с этими потоками.

Совокупность испытаний M-образцов называется M опытами. В каждом из таких опытов, вследствие однородности напряженного и деформированного состояний M-образца, внутренние параметры НДС могут быть определены по параметрам поведения границы образца. Поэтому в M-опытах используются процессы, в которых форма и размеры образцов, а также условия нагружения на их границе позволяют оценить параметры НДС внутри деформируемого тела. При этом связь внешних и внутренних параметров НДС устанавливается на основании математической постановки задачи о движении материала в деформируемом образце и ее решения.

1.5.3.Математическая постановка краевых задач

Всоответствии с определением в пп. 1.1.4 математическая постановка краевых задач МСС включает запись замкнутого множества уравнений и краевых условий. Для выполнения первой части постановки задачи необходимо сначала установить перечень независимых параметров, которые определяют НДС деформируемого тела. В эйлеровых координатах такими параметрами являются лагранжевы координаты (1.2.9), с помощью которых можно рассчитать тензор

221

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

напряжений (1.5.13). Если принять во внимание, что якобиан (1.2.20) и вспомо-

гательный вектор (1.2.94) также определяются законом движения (1.2.9), то становится очевидной зависимость вектора скорости в (1.2.95) от лагранжевых координат. Опуская промежуточные уравнения связи якобиана (1.2.20) и вспомогательного вектора D (1.2.94) с лагранжевыми координатами для трехмерного движения, устанавливаем, что в основных уравнениях (1.5.13) и (1.2.95) девять скалярных уравнений включают двенадцать скалярных неизвестных величин: σik, Li, Vi. Для замыкания множества необходимо вспомнить, что тензором напряжения может быть не любой тензор второго ранга, а лишь тот, который удовлетворяет уравнению движения (1.4.16). Однако в этом уравнении имеется дополнительная неизвестная величина – плотность ρ. Теперь двенадцать скалярных уравнений включают тринадцать неизвестных величин и множество уравнений не является пока замкнутым. Для замыкания множества добавим еще одно скалярное уравнение неразрывности среды (1.2.143), связывающее плотность и скорость и не вносящее дополнительных неизвестных величин. Полученное замкнутое множество уравнений будем называть основным множеством (табл. 4).

При необходимости к основному множеству всегда можно добавить требуемое количество уравнений, не нарушающих его замкнутости. Так, при определении параметровдеформированногосостояниякосновномумножествуподключаются(1.2.4)

для расчета вектора перемещения U , (1.2.4) или (1.2.70) для расчета тензора деформации TL или Tε, (1.2.137) для расчета тензора скоростей деформаций Tξ. Вместе с основным множеством перечисленные уравнения образуют новое замкнутое множество уравнений, содержащее 28 скалярных уравнений и такое же количество скалярных неизвестных, которые используются в математической постановке изотермических задач ТП. Для неизотермических процессов к этим уравнениям следует

Таблица 4. Уравнения основного замкнутого множества

222

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

добавить уравнение теплопроводности (1.4.61), в котором все теплофизические параметры должны быть заданы. В этом случае к 28 неизвестным величинам добавляется температура θ и замкнутое множество содержит 29 скалярных уравнений.

При решении некоторых задач МСС основное множество уравнений удобно записывать не через вектор скорости V , как это показано в табл. 4, а через вектор перемещения U . В этом случае в основном множестве остается уравнение (1.5.13), а уравнения (1.2.92) и (1.4.5) (табл. 4) заменяются уравнениями (1.2.4) и (1.2.145) соответственно. При этом последнее уравнение необходимо переписать в эйлеровых координатах. Интегрируя (1.2.145), имеем ρJL = с. Для

Кроме того, в уравнении движения (1.4.16) вместо вектора скорости нужно записать его значение, рассчитываемое по формуле (1.2.90). Окончательно получаем основное замкнутое множество уравнений в перемещениях (табл. 5).

Так же как и в предыдущем случае, к основному множеству уравнений, представленных в табл. 5, можно добавлять необходимое количество других уравнений, не нарушающих замкнутость множества.

Для выполнения второй части математической постановки задачи необходимо оговорить значения параметров, входящих в замкнутое множество уравнений, в начальный момент времени (начальные условия) и на границе области движения сплошной среды (граничные условия). Совокупность начальных и граничных условий называется краевыми условиями.

Таблица 5. Основное множество уравнений в перемещениях

223

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Из теории дифференциальных уравнений известно, что при интегрировании множества дифференциальных уравнений, содержащих производные искомой функции одного аргумента наивысшего порядка n, их общее решение зависит от n констант интегрирования. При интегрировании замкнутого множества уравнений, связанного с постановкой краевой задачи, количество таких констант зависит от наивысшего порядка производных по времени t и наивысших порядков производных по эйлеровым координатам Ei. Общее количество соотношений в краевых условиях должно быть равно общему количеству констант интегрирования. Причем эти условия могут быть заданы как для самих параметров, входящих в множество, так и для производных параметров по аргументам порядка не выше n – 1.

Исходя из изложенного, подсчитаем количество соотношений в краевых условиях, необходимых для определения констант интегрирования основного замкнутого множества уравнений (табл. 4). Проще всего это можно сделать путем последовательных подстановок уравнений (1.5.13), (1.2.92), (1.4.5) основного множества в (1.4.16), приводящих множество четырех тензорных уравнений к одному тензорному уравнению. Тогда относительно лагранжевых координат Lk полученное дифференциальное уравнение будет содержать производные второго (наивысшего) порядка по времени t и по эйлеровым координатам Ei. Значит, в N-мерном эйлеровом пространстве количество констант интегрирования n = 2(1 + N). Это же число определяет количество необходимых соотношений в краевых условиях. При этом отмечаем, что две константы были связаны с интегрированием по времени. Значит, начальные условия должны содержать два соотношения. Одно из них определяет значение лагранжевых координат в начальный момент времени t = t0, когда Li = Ei, другое – значение частной про-

изводной ∂Lk ∂Ei

ния должны определяться условиями в каждой точке границы S области Ω движения сплошной среды. В процессе движения среды пространственные координаты граничных точек в общем случае изменяются, а лагранжевы координаты, исходя из определения этих точек (п. 1.3) с учетом (1.2.10), остаются неизменными. Поэтому обычно границу области связывают с интервалом изменения

*Соотношение (1.5.19) следует рассматривать лишь как удобное математическое, но не физи-

ческое равенство.

224

На этой границе производные ∂Lk должны принимать значения, которые

∂Ei

задают в соответствии с априорными или апостериорными представлениями

и граничными (1.2.170) кинематическими условиями для вектора скорости – ус ловия С. Если последние условия заданы на всей границе области, то, как отмечалось ранее (пп. 1.2.8), S = Sv.

Вместо кинематических условий (1.5.20) и (1.2.170) для отдельных задач удобнее записывать статические начальные условия

и граничные статические (нормальные и касательные напряжения) условия (1.3.50) – условия Н. В случае, когда последние условия заданы на всей границе области, имеем S = Sσ (п. 3.5). Наряду с кинематическими или статическими граничными усло-

225

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Таблица 7. Механические краевые условия основного множества уравнений в перемещениях

виями при решении задач часто задают смешанные граничные условия, когда или на поверхности Spv задаются нормальное напряжение (1.3.52) и тангенциальная скоY рость (1.2.175) – условия ННТС, или на поверхности Sτv задаются касательное наY пряжение (1.3.53) и нормальная скорость (1.2.171) – условия КННС.

Совокупность всех величин, характеризующих значения кинематических и статических параметров в начальный момент времени и на границе области движения среды, называется механическими краевыми условиями. Различные варианты записи механических краевых условий для параметров основного множества уравнений приведены в табл. 6.

В общем случае при решении задач ОМД граница области движения металла может состоять из участков, на которых заданы С-, Н-, ННТС- и КННСграничные условия:

При расширении основного множества уравнений введением дополнительных уравнений и параметров движения среды для последних также записываются краевые условия, если эти условия не являются следствием механических краевых условий основного множества уравнений (табл. 6). Так, при добавлении к основному множеству (табл. 4) уравнений (1.2.4) могут быть использованы краевые условия (табл. 6) либо краевые условия основного множества в перемещениях (табл. 7), где, в отличие от табл. 6, вместо С-, ННТС- и КННСусловий в скоростях используются П , ННТП и КННП условия в перемещениях

226

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

соответственно. Условия табл. 7 применяются при решении основного множества уравнений в перемещениях (табл. 5). При решении неизотермических задач в их математической постановке наряду с уравнением (1.4.61) рассматриваются температурные краевые условия. В зависимости от типа решаемой задачи это могут быть граничные условия первого, второго, третьего или четвертого рода, рассматриваемые для нестационарных задач вместе с начальными температурными условиями. Последние, как и ранее, означают распределение рассматриваемого параметра, в данном случае – температуры, в начальный момент времени

Граничные условия первого рода определяют распределение температуры θn на границе SI объема Ω тела M в любой момент времени:

При этом должна соблюдаться совместимость (1.5.24) с условием (1.5.23) при подстановке в последнее координат Ei точек s границы SI, а в первое t = t0.

Граничные условия второго рода связаны с вектором теплового потока (1.4.58), проекция qn которого на внешнюю единичную нормаль n к поверхности SII задана на этой поверхности. Учитывая, что qn = q n и производная температу-

Граничные условия третьего рода задаются на поверхности SIII, через которую осуществляется значимый конвективный теплообмен между исследуемым объемом Ω тела M и окружающей его средой:

где α – коэффициент теплообмена; θс – температура окружающей среды. Эти условия применяются в задачах стационарного конвективного теплообмена.

Граничные условия четвертого рода на границе SIV позволяют учитывать нестационарный теплообмен контактируемых α- и β-сред, когда температура их соприкасающихся поверхностей Sαβ = SIV одинакова:

227

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

Ясно, что при решении уравнения теплопроводности (1.4.69) для композит-

k

ной среды M = Mα температурные граничные условия на стыке Sαβ ее ком-

α=1

понент должны быть представлены в виде (1.5.27).

Приведенная выше математическая постановка краевых задач является общей, если учесть, что, как отмечалось ранее, к основному замкнутому множеству уравнений с необходимыми краевыми условиями всегда, когда требуется, можно добавить уравнения с соответствующими краевыми условиями без нарушения замкнутости получаемого при этом множества уравнений.

Следует отметить, что в приведенных постановках задач мы не использовали ограничений, накладываемых на тензор деформаций Tε и тензор скоростей деформаций Tξ. Вид этих ограничений (1.2.88) и (1.2.166) для обоих тензоров по форме одинаков. Ранее отмечалось, что при решении задач в перемещениях или скоростях тензор Tε или тензор Tξ определяется по формуле О. Коши (1.2.70) или Дж. Стокса (1.2.137) соответственно, которые с точностью до символики также совпадают, и вследствие безусловного выполнения тождества (П1.89) такое определение Tε и Tξ приводит к тождественному выполнению условий Б. Сен-Венана (1.2.88) или (1.2.166). Этим объясняется отсутствие последних уравнений в приведенных математических постановках краевых задач.

Если решение задачи основано на постановке в деформациях через тензор Tε или в скоростях деформаций через тензор Tξ, то соответствующие условия Б. Сен-Венана должны учитываться в замкнутом множестве уравнений. Пример таких множеств без учета инерционных и массовых сил для сред, свойства которых описываются определяющими уравнениями (1.5.2) или (1.5.4), приведен в табл. 8. При этом тензор напряжений представлен в виде (1.4.19) с помощью тензора TΦ функций напряжений Э. Бельтрами для безусловного выполнения уравнения равновесия (1.4.18). С использованием тензора TΦ уравнения (1.5.2) и (1.5.4) принимают соответствующий вид:

228

1.5. РЕОЛОГИЯ КОМПОЗИТНЫХ СРЕД

Если на границе области движения среды заданы кинематические или смешанные граничные условия, то сложность реализации постановки задач с уравнениями табл. 8 связана с интегрированием формул Е. Чезаро (1.2.89) или (1.2.167).

Задачи к пп. 1.5.3

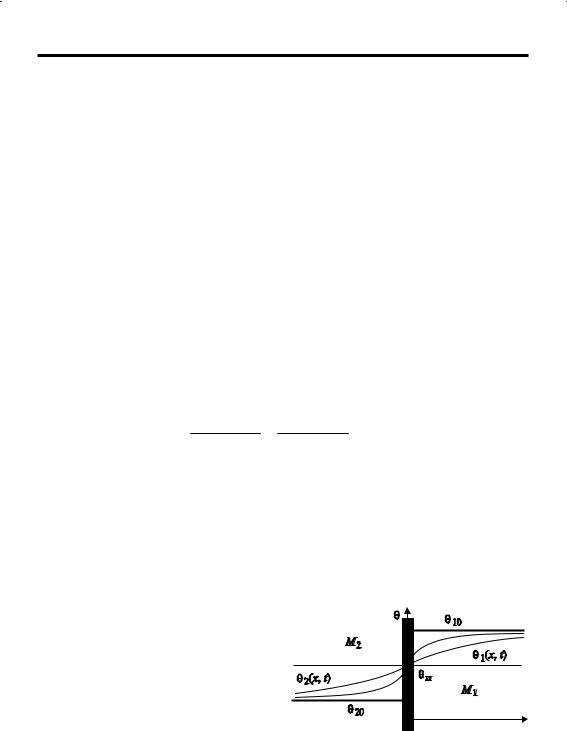
Задача 1.5.3.1. Найти распределение температуры в произвольный момент времени для двух контактирующих полуограниченных тел М1 и М2 (рис. 49), равномерно нагретых до температуры Τ10 и Τ20 соответственно, приведенных в соприкосновение в момент времени t = 0, при начальных условиях Τ1(x, 0) = Τ10, Τ2(x, 0) = Τ20 и при граничных условиях четвертого рода:

где Τ1(+0, t) и Τ2(–0, t) – предельные значения температуры при стремлении аргумента х к нулю справа и слева; Νi – коэффициенты теплопроводности тел Мi. В качестве дополнительного вводится условие затухания тепловых возмущений при х = ρ φ:

ωΤ1(φ, t) ωΤ2 (φ, t) 0. ωx ωx

Решение. По условию задачи температура в любой точке рассматриваемых неподвижных тел зависит только от двух переменных: координаты х и времени t. Запишем уравнение теплопроводности (1.4.62) без внутренних источников тепла для тела М1 (i = 1; t > 0; x > 0) и тела М2 (i = 2; t > 0; x < 0):

229

1. МЕХАНИКА СПЛОШНЫХ КОМПОЗИТНЫХ СРЕД

ны краевые условия и записано замкнутое относительно θi множество уравнений) выполняется с помощью интегрального преобразования П. С. Лапласа и представляется в виде

где приращение температуры Δθ = θ10 – θ20; критерий

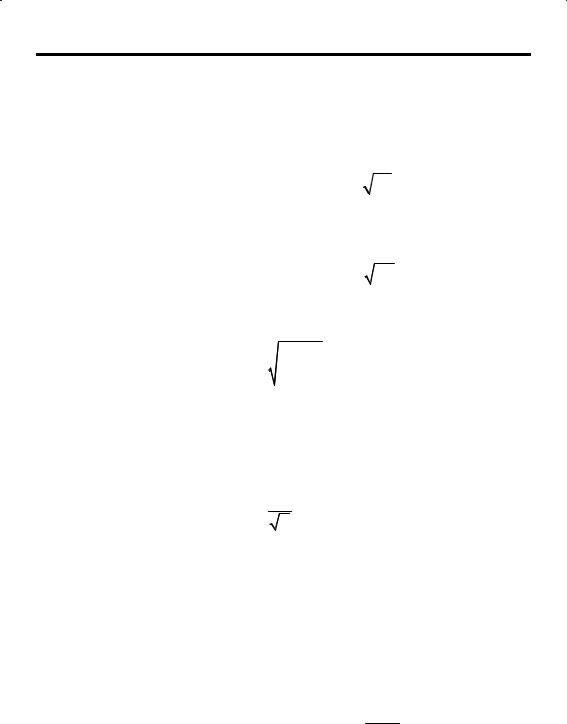
равен отношению тепловой активности первого тела (числитель) к аналогичной активности второго тела (знаменатель); ci – удельные теплоемкости тел Мi; ρi – плотность каждого из тел. Интеграл вероятности, называемый функцией ошибок К. Гаусса, в формуле

erf(z) = 2 ∫z e−uz du,

π 0

имеющий частные значения erf(0) = 0, erf(∞) = 1, и связанная с этим интегралом функция erfс(z) = 1 – erf(z) задаются таблично в математических справочниках, связанных с курсом теории вероятности.

Рассмотренная задача может быть использована для приближенного анализа распределения температуры (на рис. 49 – пунктирные линии) в окрестности контакта между нагретым телом и инструментом в процессах ОМД.

Из полученного решения следует, что на поверхности контакта температура θп сразу же после соприкосновения двух тел устанавливается равной

KΔθ

θп = θ1(+0, t) = θ2(–0, t) = θ20 + 1+ K

230