1.5. Квантовая статистика электронов в кристаллах

Известно, что классическая теория электронного газа в металлах не смогла объяснить три явления:

электронный газ практически не поглощает тепла при нагревании, то есть не обладает теплоемкостью;

из классической теории следует, что при абсолютном нуле температуры энергия электронов должна быть равна нулю, а электрическое сопротивление металла - нулю;

согласно классическим представлениям длина свободного пробега электронов в металлах должна составлять величину около 0,5 нм, что соответствует параметру кристаллической решетки большинства металлов. На самом деле она равна 10...100 нм, при высоких температурах - немного меньше.

Перечисленные трудности удалось преодолеть с помощью квантовой теории, разработанной Я. И. Френкелем - А. Зоммерфельдом в 20-х годах прошлого столетия. Квантовая статистика базируется на следующих положениях квантовой теории атомов и электронов.

1.5.1. Уровень Ферми. Работа выхода электронов

Согласно принципу Паули в одном электронном состоянии может находиться не более одного электрона. Поэтому при температуре абсолютного нуля n свободных электронов в кристалле с металлической проводимостью займут n/2 наиболее низких энергетических уровня.

Максимальное значение энергии, которую может иметь электрон в кристалле при температуре Т=0 К называют энергией Ферми (или уровнем Ферми) и обозначают W_F (рис. 1.14). Значение W_F=5...9 эВ.

Для удаления электрона с уровня Ферми за пределы металла или полупроводника следует совершить работу, которая носит название термодинамической работы выхода, =W₀-W_F (рис. 1.14, а). Работу, необходимую для удаления электрона с уровня зоны проводимости W_C за пределы полупроводника (рис. 1.14, б), называют полной работой выхода, _п=W₀-W_C. Работа выхода обычно измеряется в электронвольтах.

1.5.2. Функции распределения электронов по энергиям

В квантовой теории вероятность заполнения энергетических состояний электронами определяется функцией распределения Ферми- Дирака:

, (1.9)

где W - энергия уровня, вероятность заполнения которого определяется при температуре T; k - постоянная Больцмана.

Системы микрочастиц, свойства которых описываются распределением Ферми-Дирака (1.9), называются вырожденными.

При Т=0 график функции Ферми имеет вид, изображенный на рис. 1.15, а.

Из рис. 1.15, а и формулы (1.10) при Т=0 вытекают следующие соотношения:

f(W, 0)=1 для W<W_F, (1.10а)

f(W, 0)=0 для W>W_F, (1.10б)

f(W, 0)={0,1} для W=W_F. (1.10в)

При нагревании металла электронам сообщается тепловая энергия, величина которой определяется произведением kT. Значение этой энергии невелико. Например, при комнатной температуре (около 300 К) значение тепловой энергии электронов определяется величиной W_т=0,026 эВ. Однако за счет теплового возбуждения существует вероятность того, что некоторые электроны с энергией, близкой к энергии уровня Ферми, начинают заполнять состояния с более высокой энергией. В результате график функции Ферми при Т=0 теряет ступенчатую форму и становится более пологим, как это показано на рис. 1.15, б. Из формулы (1.9) для Т>0 вытекают следующие соотношения:

f(W, Т)1 дляW<W_F, (1.11а)

f(W, Т)0 дляW>W_F, (1.11б)

f(W, Т)=1/2 для W= W_F. (1.11в)

Из соотношения (1.11в) следует, что вероятность "нахождения" электрона на уровне Ферми составляет 0,5.

При выполнении условия W-W_F >>kT выражение (1.9) для функции распределения Ферми-Дирака переходит в закон распределения Больцмана, т.е:

. (1.12)

Распределение Больцмана широко используется при расчетах концентрации электронов в полупроводниках.

Следует подчеркнуть, что средняя энергия электронов в металлическом кристалле с ростом температуры практически не изменяется, поскольку в результате нагрева возбуждается лишь малая часть электронов, имеющих энергию, близкую к энергии уровня Ферми (около 1). Кстати, это обстоятельство объясняет малую теплоемкость электронного газа в кристаллах. Из сказанного также следует, что согласно принципу Паули в процессе электропроводности могут принимать участие не все свободные электроны, а только небольшая их часть, имеющая энергию, близкую к энергии уровня Ферми. Только эти электроны способны изменять свое состояние под действием внешнего электрического поля, приложенного к кристаллу.

Выражение для общего числа состояний, которые могут быть заняты электронами на разрешенных уровнях энергии в металлическом кристалле найдем, воспользовавшись функцией распределения Ферми- Дирака (1.9).

Количество энергетических состояний электронов dn, приходящихся на интервал энергий dW, определяется из соотношения

dn=N(W)f(W)dW, м^-3, (1.13)

где N(W) - плотность разрешенных состояний, приходящихся на единичный интервал энергии в единице объема кристалла, м^-3Дж^-1; f(W) - функция Ферми-Дирака.

Подставим в формулу (1.13) значение N(W) из (1.7) и f(W) из (1.9). Учитываем, что при Т=0 в интервале энергий от W=0 до W=W_F значение функции распределения f(W) равно единице. В результате интегрирования формулы (1.13) в пределах от W=0 до W=W_F, получим соотношение для расчета общего количества состояний n:

. (1.14)

В результате интегрирования получаем, что

, м^-3. (1.15)

Из этого выражения можно получить формулу для расчета значения энергии уровня Ферми в металле при Т=0 в виде

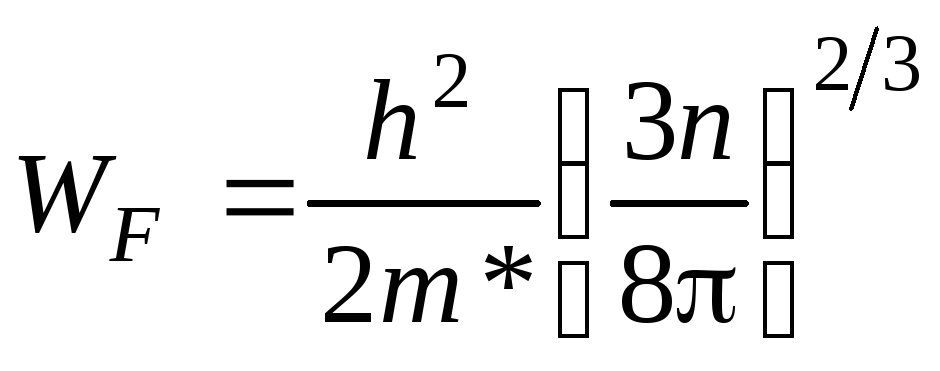, Дж. (1.16)

Пример. Рассчитаем по формуле (1.16) значение энергии уровня Ферми для одновалентной меди, характеризующейся плотностью электронного газа, численно равной количеству атомов, содержащихся в 1 м³ меди. Количество атомов N, содержащихся в 1 м³ вещества рассчитаем по формуле

, м³, (1.17)

где А=6,0210²⁶ кмоль^-1 - число Авогадро; р - плотность вещества, кг/м³; M - молярная масса вещества, кг/кмоль.

Для меди p=8,910³ кг/м³, M=64 кг/кмоль. Следовательно, количество атомов и, соответственно, количество свободных электронов в 1 м³ меди составляет величину N=n=(6,0210²⁶)(8,910³)/64=8,3710²⁸ м^-3. Подставляя это значение n в формулу (1.16) и, учитывая, что 1 Дж=6,240¹⁸ эВ, получим для величины энергии уровня Ферми W_F в меди значение 7,98 эВ.