Малышев Вычислительная математика EQ3

2

УДК 681.322(07)

Малышев Р. А. Вычислительная математика: Учебное пособие/РГАТА. – Рыбинск, 2008. – 77 с.

В настоящем пособии рассматриваются вопросы об особенностях математического моделирования и теоретические основы вычислительных методов как его инструмента. Рассмотрены методы обработки данных: интерполяция, аппроксимация, сглаживание, вычисление производных и интегралов.

Подготовлено на кафедре «Вычислительные системы» Рыбинской государственной авиационной технологической академии им. П. А. Соловьева в качестве учебного пособия для студентов специальности 230101 «Вычислительные машины, комплексы, системы и сети» направления 230100 «Информатика и вычислительная техника».

РЕЦЕНЗЕНТЫ:

Кафедра информационного сервиса Костромского государственного университета им. Н. А. Некрасова.

Заведующий ПЦК информатики Рыбинского полиграфического колледжа, программист Смирнов В. Б.

4

5.4.Конечно-разностная аппроксимация производных

5

ВВЕДЕНИЕ

Процесс научного познания часто приводит к количественным результатам. Именно эта количественная природа научных и технологических задач вызывает необходимость обработки числовой информации. В действительности ключ к пониманию многих задач заложен в том, насколько продуманно представлены описывающие их числовые данные. Напротив, плохое представление данных часто приводит к заблуждениям, неправильной интерпретации и даже к ошибкам исследователей. Из-за больших вычислительных возможностей часто используют для анализа экспериментальных данных персональный компьютер (ПК) [1].

В настоящее время практически все потоки цифровые, в связи с этим необходима обработка цифровой информации. Часто имеется набор данных (таблица, аналитическое выражение), полученный экспериментальным или расчетным или теоретическим путем, который необходимо обработать, например, найти экстремумы, угол наклона кривой, площадь фигуры, ограниченной линиями. Этим вопросам и посвящено данное пособие.

1. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ

Во всех случаях обработка информации сводится к математической обработке некоторых функциональных зависимостей, исходя из этого, к общим для всех методов можно отнести: сглаживание цифровой информации, дифференцирование, интегрирование, поиск экстремумов и т. д.

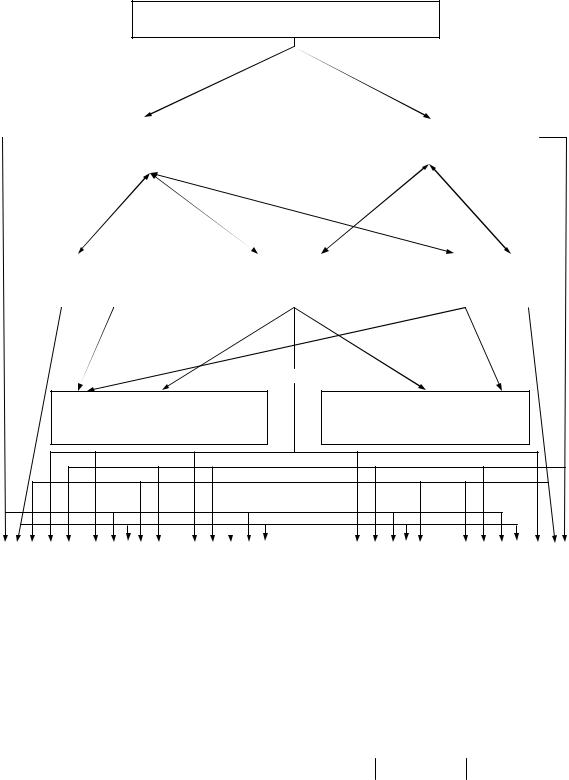
Виды представления данных и методы их обработки приведены на рис. 1.1.

1.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. КЛАССЫ ФУНКЦИЙ

На отрезке [a, b] вещественной оси будем рассматривать множество В, элементы которого непрерывные функции.

Если f(x) и g(x) – две функции из этого множества, а с – вещественное число, то cf(x) и f(x) + g(x) тоже являются его элементами. B – называется линейным пространством, а его элементы – точки линейного пространства [2].

Расстояние ρ(f, g) между двумя точками пространства или метрика – это вещественная функция пары точек, принимающая неотрицательные значения и удовлетворяющая следующим аксиомам метрики:

а) ρ(f, g) = 0, тогда и только тогда, когда f = g;

6

б) ρ(f, g) = ρ(g, f) (симметрия);

в) ρ(f, r) ≤ ρ(f, g) + ρ(g, r) (неравенство треугольника).

Исходные данные

Интегрирование:

Рис. 1.1. Представление и методы обработки исходных данных процессов

Линейное пространство с метрикой называется метрическим пространством.

В множестве В введём расстояние формулой:

ρ( f , g ) = f (x) − g (x) = max x [a, b] f ( x) − g ( x) .

Это расстояние удовлетворяет всем аксиомам метрики и делает В метрическим пространством.

7

Каждый элемент f(x) метрического пространства можно характеризовать числом ||f(x)|| (расстоянием до нулевого элемента), называемым нормой элемента

ρ( f , 0) = f ( x) − 0 = max x [a, b] f (x) − 0 = max f ( x) .

Обозначим Cm[a, b] классы функций в пространстве В, имеющие на отрезке [a, b] непрерывные производные до m-го порядка включительно, т. е., если f(x) C3 то f ′(x), f ″(x), f ″′(x) – непрерывны на [a, b]. Если непрерывны производные до (m – 1)-го порядка, а m-е производные кусочнонепрерывны, то такой класс обозначим C(m)[a, b]. Значения функций f(x) и их производных f (p)(x) из этих классов можно представить в виде разложений по формуле Тейлора [2]:

ζ– точка на множестве В.

1.2.ПРОСТРАНСТВО МНОГОЧЛЕНОВ

Многочлены Pn(x) = a0 + a1x + ... + anxn являются элементами пространства В. Функции 1, x, ... , xn , из которых конструируются многочлены степени n, линейно независимы, т. е. Pn(x) ≠ 0, если хотя бы один коэффициент ak ≠ 0. Число этих функций n + 1 (степени от 0 до n) – есть размерность пространства Мn, а сами они образуют базис последнего.

Вообще, базисом n + 1-мерного функционального пространства может быть любая совокупность n + 1 его линейно независимых функций. Так, во множестве Мn базисом является следующая система функций.

где отрезок [a, b] разбивается на n частей точками xk, a = x0 < x1 < ... < xn = = b, k = 0, ... , n.

8

Функции Фk(x) линейно независимы и образуют базис в Мn, т. е. любой многочлен из Мn можно представить в виде Pn(x) = c0Ф0(x) + ... +

+ cnФn(x).

Интерполяция – нахождение значения функции в некоторой промежуточной точке по отношению к заданным (табличным) данным.

Аппроксимация – представление или приближение заданных данных кривыми.

Экстраполяция – отыскание значения функции в некоторой удаленной точке за пределами отрезка, на котором определена функция.

2.МЕТОДЫ ИНТЕРПОЛЯЦИИ

2.1.Интерполяция по Лагранжу

Задачи аппроксимации функций многочленами (а затем и сплайнами) характеризуются их содержанием, точностью приближения и спецификой приближения. Простейшим методом аппроксимации является интерполя-

ция [1 – 3].

Пусть в узлах xk [a, b] заданы значения функции fk = f(xk), k = 0, ... , n. Требуется найти многочлен Pn(x) из множества Мn, удовлетворяющий условиям Pn(xk) = fk, k = 0, ... , n. Решение задачи даёт интерполяционный многочлен Лагранжа: Ln(x) = f0Ф0(x) + ... + fnФn(x) [2].

В знаменателе значения в скобках – числа, следовательно, значение всего знаменателя – число. Таким образом, если раскрыть скобки в числителе, то получится полином n-го порядка от х, т. к. в числителе содержится n сомножителей 1-го порядка. Следовательно, интерполяционный многочлен Лагранжа – это обычный полином n-го порядка со специфической формой записи.

При интерполяции по Лагранжу задают n + 1 табличное значение (xi, fi), где i = 0, 1, .. , n. Предположим, что точки (xi, fi) принадлежат кривой

9

f = f(x) в интервале x0 ≤ x ≤ xn. Интерполяционный многочлен для этого метода имеет вид:

Ln(x) = f0Ф0(x) + f1Ф1(x) + ...+ fnФn(x),

где все Фj(x) – многочлены степени n, коэффициенты которых можно найти с помощью n + 1 уравнений: Ln(xi) = fi при i = 0, 1, .. , n.

В результате получим систему уравнений:

(т. е. Фj(xj) = 1), то выписанные выше уравнения будут удовлетворены. Это условие означает, что любой многочлен Фj(x) равен нулю при каждом xi кроме xj. Следовательно, в общем случае многочлен Фj(x) имеет вид:

Фj(x) = Cj(x – x0) (x – x1) ... (x – xj – 1) (x – xj + 1) ... (x – xn).

Так как Фj(xj) = 1, то коэффициент Cj определяется выражением:

Введя обозначения:

Lj(x) = (x – x0) (x – x1) ... (x – xj – 1) (x – xj + 1) ... (x – xn),

можем записать полученный многочлен в более компактном виде:

10

Основным преимуществом лагранжевой интерполяции является её простота и быстрота.

Решить задачу аппроксимации табличных значений можно также с помощью наилучших приближениях непрерывных функций: равномерного (чебышевского) и среднего квадратического. Они весьма сложны по реализации. Один из путей уменьшения трудностей состоит в построении формул аппроксимации многочленами Pn(x), только похожих на наилучшие, близких к ним (рассмотрены ниже). Другой путь заключается в решении задач приближения не на отрезке [a, b], а на дискретном множестве

точек {xν, ν = 1, ... , N*} [a, b], N* > n + 1, т. е. искомый многочлен Pn(x)

должен максимально приближаться к функции, заданной точками. Погрешностью метода аппроксимации называется расстояние между

приближающим многочленом и аппроксимируемой функцией в заданной метрике. Если обозначить через Rn(x) = Pn(x) – f(x) остаточный член аппроксимации, то погрешность будет ||Rn(x)||. Эта величина зависит от степени многочлена и дифференциальных свойств функции f(x), т. е. от максимального порядка непрерывной производной. При увеличении степени многочлена получаем последовательность (ряд) аппроксимаций. Если ||Rn(x)|| → 0, при n → ∞, то аппроксимирующий процесс сходится, в противном случае – расходится. Сходимость интерполяционных многочленов Лагранжа гарантируется далеко не во всех случаях.

Погрешность в точке xk [x0, xn] [3]:

n

R(x) = |f (x) − Ln (x)| ≤ (M n + 1/(n +1)!) ∏ (x − xi ) ,

i = 0

где Mn + 1 = max|f (n + 1)(x)| – максимальное значение (n + 1) производной исходной функции f(x) на отрезке [x0, xn], т. е. функция должна быть дифференцируема n + 1 раз.

Пример 1 [3].

Дана таблично заданная функция

Требуется найти у при х = 4. В данном случае n = 3. Запишем функцию Лагранжа подробно: