
Малышев Вычислительная математика EQ3
.pdf
11
|
|
|
( x − x0 )( x − x1 )( x − x3 ) |
(x − x0 )( x − x1 )( x − x2 ) |
|
|||||||||||||||
+ y2 |
|
|
|
|
|
+ y3 |
|
|
= |
|||||||||||
( x − x )( x − x )( x − x ) |
( x − x )( x − x )( x − x ) |
|||||||||||||||||||
2 |
0 |
2 |
1 |
2 |
3 |
|
|
3 |
0 |
3 |
|
1 |
3 |
2 |
|
|||||
= −1 |
(4 −1)(4 − 2)(4 − 6) |
|
− 3 |
(4 − 0)(4 − 2)(4 − 6) |
+ |
|
|
|
||||||||||||
(0 −1)(0 − 2)(0 − 6) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
(1 − 0)(1 − 2)(1 − 6) |
|
|
|
|
||||||||||||
+3 |
(4 − 0)(4 −1)(4 − |
6) |
+1187 |
(4 − 0)(4 −1)(4 − 2) |
= 255. |
|
|
|||||||||||||
(2 − 0)(2 −1)(2 − |
6) |
(6 − 0)(6 −1)(6 − 2) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
В данном примере отсутствует информация о значении четвертой производной исходной функции, поэтому оценить погрешность не представляется возможным.
Пример 2 [3].
Дана функция y = 
 x . Найти погрешность интерполяции функции при х = 115. Запишем:
x . Найти погрешность интерполяции функции при х = 115. Запишем:
x |
100 |
121 |
144 |
|
|
|
|
y |
10 |
11 |
12 |
|
|
|
|
Имеем всего три узла интерполяции, n = 2. Оценим максимальное значение третьей производной для оценки погрешности
y′ = x−1 2 / 2; y′′ = −x−3 2 / 4; y′′′ = 3x−5
2 / 4; y′′′ = 3x−5 2 / 8 ;
2 / 8 ;
M 3 = max y′′′ = 3(100)−5 2 / 8 .
2 / 8 .
Погрешность при интерполяции по трем узлам будет:
R ≤ 3(100)−5 2 / 8 (115 −100)(115 −121)(115 −144) /(1 2 3) ≈ 1, 6 10−3 .
2 / 8 (115 −100)(115 −121)(115 −144) /(1 2 3) ≈ 1, 6 10−3 .
Ошибка получилась достаточно малой, а само значение у(115) можно найти самостоятельно и проверить его по таблицам или на калькуляторе.
2.2. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
Часто исходные данные представляются в виде таблиц. Это связано с тем, что они получены экспериментально. Сущность интерполяции состоит в отыскании значения функции в некоторой промежуточной точке по отношению к табличным данным.
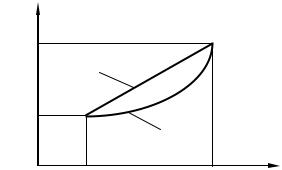
Простейший вид интерполяции является линейная интерполяция [2]. Этот простейший метод приближения функций приведён на рис. 2.1. Он широко применяется на практике. В частности, различные таблицы составляются так, чтобы промежуточные значения функции с принятой точностью можно было вычислить с помощью линейной интерполяции.
12
f(x)
fk + 1
P1(x)
fk
f(x)
0 |
xk |
xk + 1 |
x |
Рис. 2.1. Линейная интерполяция
В основе линейной интерполяции лежит аппроксимация кривой на участке между точками (xk, fk) и (xk + 1, fk + 1) прямой, проходящей через те же точки. Уравнение прямой можно представить в виде:
|
|
(f − fk ) |
(fk +1 − fk ) |
||||
|
|
|
= |
|
|
, |
|
|
|
|
|||||
|
|
(x − xk ) |
(xk +1 − xk ) |
||||
или в виде: |
|
|
|
|
|||
|
|
fk (x − xk +1 ) − fk +1 |
(x − xk ) |
||||
f = |
|
|
|
. |
|||
|
− xk +1 ) |
|
|||||
|
|
( xk |
|
|
|
||
Таким образом, зная два табличных значения fk и fk + 1, соответствующих xk и xk + 1, с помощью указанных формул можно найти значения функции f при любом значении x в интервале [xk, xk + 1].
Если обозначить – xk и ввести параметр
0 ≤ u ≤ 1 (из формулы Лагранжа Ln(x) = f0Ф0(x) + ... + fnФn(x)), то базисные функции будут Ф0(x) = (1 – u), Ф1(x) = u, и интерполяционная формула принимает вид: L1(x) = (1 – u)fk + ufk + 1.
Процесс получения оценки погрешности разбивается на четыре этапа [2]. Пусть f(x) C(2) (непрерывна только первая производная).
Остаточный член интерполяции
R1 (x) = L1 (x) − f (x) = (1 − u) fk + ufk +1 − f (x).
Значения fk, fk + 1 заменим разложениями по формуле Тейлора при m = 2:
xk
fk = f (x) − huf ′(x) + ∫ (xk − ζ)f ′′(ζ)dζ;
x
13
|
xk +1 |
|
′ |
∫ |
′′ |
fk +1 = f (x) + h(1 − u) f (x) + |
(xk +1 − ζ)f (ζ)dζ . |
|
|
x |
|
Подставив эти выражения в R1(x), получаем интегральное представление остаточного члена интерполяции:
x xk +1
R1 (x) = (1 − u) ∫ (ζ − xk )f ′′(ζ)dζ + u ∫ (xk +1 − ζ)f ′′(ζ)d ζ.
xk x
Вкаждом из интегралов сделаем замену переменной интегрирования
ζ= xk + hτ, 0 ≤ τ ≤ 1. Тогда:
|
|
|
|
|
|
u |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
R1 (x) = h2 [(1 − u)∫τf ′′(ζ)d τ + u ∫(1 − τ)f ′′(ζ)d τ]. |
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
u |
|
|
|
|
|
|
|
|
Отсюда следует: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
u |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|R1 (x)| ≤ h2 [(1 − u)∫τ|f ′′(ζ)|d τ + u ∫(1 − τ)|f ′′(ζ)|d τ]. |
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
u |
|
|
|
|
|
|
|
|
Заменяем f (ζ)| на max |
|
f (x) |
|
x |
, x . |
|
|
|
|
|
||||
|
|
|
|
|
′′ |
|
′′ |
|
|
k |
k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Неравенство от такой |
|
замены |
усиливается. |
Вынося |
постоянную |
|||||||||
|
|
f (x) |
|
x |
, x за знаки интегралов, получаем: |
|
|
|
|
|
||||||
|
|
′′ |
|
k |
k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|R1 (x)| ≤ h2[(1 − u)∫τd τ |
+ u ∫(1 − τ)d τ ] ||f ′′(x)||[x |
, x |
] . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k +1 |
|
|
|
|
|
|
0 |
|
|
|
|
u |
|
|
|
|
|
|
|
|
Вычисляя интегралы, находим поточечную оценку погрешности (в |
||||||||||||||
зависимости от x) в виде: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|R (x)| ≤ 0,5 h2 |
u (1 − u) ||f ′′(x)|| |
|
] |
. |
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
[ x , x |
k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
Из последнего неравенства выводится оценка максимальной погрешности. Для этого достаточно подсчитать максимум функции (1 – u)u. Он достигается в середине отрезка при u = 0,5 и равен 0,25. Окончательно:
|| R1 (x)||[ xk , xk +1 ] ≤ 0,125 h2 ||f ′′(x)||[ xk , xk +1 ]

14
2.3. ПРИБЛИЖЕНИЯ МНОГОЧЛЕНАМИ ПЕРВОЙ СТЕПЕНИ, БЛИЗКИЕ К НАИЛУЧШИМ РАВНОМЕРНЫМ
Наряду с интерполяцией по линейной формуле, на отрезке [x0, x1] рассмотрим аппроксимацию (рис. 2.2) [2]:
P (x) = (1 − u) [f |
0 |
− h2 f ′′/16] + u[f |
− h2 f ′′/16] ; |
|
1 |
0 |
1 |
1 |
|
u = (x − xk )/h, 0 ≤ u ≤ 1, h = xk +1 − xk .
f(x)
P1(x)
 f(x)
f(x)
0 x0 x1 x
Рис. 2.2. Приближение многочленом 1-ой степени
Её погрешность для функции f(x) C(3)[a, b] даётся формулой: || R1 (x)||[ x0 , x1 ] ≤ h2 /16[||f ′′(x)||[ x0 , x1 ] + ch||f ′′′(x)||[ x0 , x1 ] ].
Причем значение второго слагаемого стремится к 0 при h → 0.
Из этого видно, что коэффициент при 
 f ′′( x)
f ′′( x)
 [x0 , x1 ] вдвое меньше, чем
[x0 , x1 ] вдвое меньше, чем
при интерполяции. Эта аппроксимация для многочленов второго порядка (f ″′(x) = 0) является наилучшим равномерным (чебышевским) приближением.
Для других функций она даёт приближение, качественно похожее на чебышевское. Второй член правой части при h → 0 есть малая более высокого порядка по сравнению с первым членом. В этом смысле построенное приближение можно назвать асимптотически наилучшим равномерным приближением.
2.4. ПАРАБОЛИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
Наряду с линейной интерполяцией интерполяции кривыми более высокого порядка – это часто используемые методы приближения функций [2]. Характеристики методов приведены в табл. 2.1.

|
|
15 |
|
|
|
|
|
|
|
Таблица 2.1. |
|
|
Методы интерполяции |
|
|
||
Вид |
Характеристики интерполяции |
|
|||
интерполяции |
Формула |
Условия |
Погрешность |
||
Линейная |
L1(x) = (1 – u)fk + ufk + 1 |
Прохождение |
≤ 0,125 h2 ||f ″(x)|| |
||
|
|
|
через две |
|
|
|
|
|
точки |
|
|
Многочленом |
P1(x) = (1 – u)[f0 – |
Прохождение |
≤ h2/16[||f ″(x)|| + |
||
1-ой степени |
– h2f0″/16] + u[f1 – h2f1″/16] |
через две |
+ch||f ″′(x)||] |
||
|
|
|
точки |
|
|
Параболическая L2(x) = f0 + (x – x0)f[x0, x1] + |
Прохождение ≤ 0,1546 (max h)2 · |
||||
|
+ (x – x0)(x – x1)f [x0, x1, x2] |
через три |
· ||f ″′(x)|| *, |
||
|
|
|
точки |
||
|
|
|
≤ |
3 / 27 · |
|
|
|
|
|
||
|
|
|
|
· (maxh)3||f ″′(x)|| |
|
Кубическая |
L3(x) = f0 + (x – x0)f[x0, x1] + |
Прохождение |
≤ K0k(maxh)4 |
||
|
+ (x – x0)(x – x1) f[x0, x1, x2] |
через четыре |
||f IV(x)||, |
||
|
+(x – x0)(x – x1)(x – x2) · |
точки |
K00 = K02 = 1/24; |
||
|
· f[x0, x1, x2, x3] |
|
K01≤ 3/128. |
||
Эрмитова |
3(x) = φ1(u)f0 + φ2(u)f1 + |
3(xk) = fk; |
≤ Kph4 – p||f IV(x)||; |
||
кубическая |
+ hφ3(u)f0′ + hφ4(u)f1′; |
′3(xk) = fk′; |
p= 0, 1, 2; |
||
|
|
|
|||
|
2 |
(1 + 2u); |
k = 0, 1. |
K0= 1/384; |
|
|
φ1(u) = (1 – u) |
|
|
||
|
φ2(u) = φ1(1 – u) = |
|
K1 = |
3/ 216 ; |
|
|
= u2(3 – 2u); |
|
K2= 1/12. |
||
|
φ3(u) = u (1– u) 2; |
|
|
|
|
|
φ4(u) = –φ3(1 – u) = |
|
|
|
|
|
–u2(1 – u). |
|
|
|
|
* – интерполируемая функция из более высокого класса гладкости, f(x) C(3)[x0, x2].
Представим интерполяционный многочлен Лагранжа
Ln(x) = f0Ф0(x) + ... + fnФn(x)
через разделенные разности:
– разделенная разность порядка 0 равна значению функции в точке
f(x0);
– разделенная разность порядка k:
f [x0, …, xk] = (f [x1, …, xk] – f [x0, …, xk – 1])/(xk – x0).
Если f (k)(x) – непрерывная, то f (x0, …, xk) = f (k)(ζ)/k!, ζ – точка на отрезке [x0, xk].

16
Тогда Ln(x) = f0 + (x – x0) f [x0, x1] +…+ (x – x0)…(x – xn – 1) f [x0,…, xn].
Интерполяционный многочлен вида P2(x) = ax2 + bx + c возьмём в форме:
L2(x) = f0 + (x – x0) f [x0, x1] + (x – x0)(x – x1)f [x0, x1, x2].
Точность приближения функции f(x) так же, как и ранее, зависит от того, к какому классу она принадлежит, и от расстояния между узлами. Обозначим h0 = x1 – x0, h1 = x2 – x1, H = max (h0, h1). Остаточный член интер-
поляции R2(x) = L2(x) – f(x) [2, 3]. Тогда, если f(x) C(2)[x0, x2], то

 R2 ( x)
R2 ( x)
 [x0 , x2 ] ≤ 0,1546H 2
[x0 , x2 ] ≤ 0,1546H 2 
 f ′′( x)
f ′′( x)
 [x0 , x2 ].
[x0 , x2 ].
Сравнивая эту оценку с оценкой линейной интерполяции, видно, что при h0 = h1 = h они практически совпадают, незначительно различаясь коэффициентами.
Если интерполируемая функция из более высокого класса гладкости,
f(x) C(3)[x0, x2], то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| R (x)|| |
, x2 |
] |
≤ ( 3 /27 ) H 3 ||f ′′′(x)|| |
, x2 |
] |
. |
|||
2 |
[ x0 |
|
|
[ x0 |
|
||||
Как видно из последнего неравенства (см. табл. 2.1), здесь порядок приближения относительно H, на единицу выше, и при малых H точность повышается. Однако дальнейшее повышение класса гладкости уже не приводит к увеличению порядка приближения относительно H или уменьшению коэффициента. Происходит насыщение интерполяционного процесса. Для многочленов первой степени этому соответствует класс C(2), второй степени – C(3), третьей – C(4).
2.5. КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
Интерполяционный многочлен вида P3(x) = ax3 + bx2 + cx + d возьмём в форме многочлена Лагранжа:
L3(x) = f0 + (x – x0) f [x0, x1] + (x – x0)(x – x1) f [x0, x1, x2] + + (x – x0)(x – x1)(x – x2) f [x0, x1, x2, x3].
Эта формула даёт примерно такую же точность приближения, что и формула параболической интерполяции для функций из классов C(2)[x0, x3] и C(3)[x0, x3]. Наивысший порядок H4 достигается, если f C(4)[x0, x3]. Так как многочлен L3 симметричен относительно индексов 0, 1 и 2, 3, то оценки погрешности будут одинаковыми для промежутков [x0, x1] и [x2, x3]:

17
||L3(x) – f(x)|| [xk , xk +1 ] ≤ K0k H4|| f IV(x)|| [x0 , xk ] ,
где K00 = K02 = 1/24; K01≤ 3/128; H = max(h0, h1, h2). Как видно, K01 < K00 = = K02. Это означает, что точность приближения на среднем звене отрезка [x0, x3] выше, чем на крайних звеньях.
Эрмитова кубическая интерполяция представлена графически на рис. 2.3 и в табл. 2.1.
f(x)
f(x)
3(x)
0 x0 x1 x
Рис. 2.3. Эрмитова кубическая интерполяция
Вывод оценок погрешности эрмитовой интерполяции принципиально не отличается от предыдущих случаев. Дополнение состоит лишь в том, что по формуле Тейлора в узлах приходится представлять не только значения функции f0, f1 , но и значения её производной f0', f1', которые входят в выражение интерполяционного многочлена 3(x). При этом, естественно, число членов в представлениях значений производной на единицу меньше.
Для интерполируемой функции f(x) C(2)[x0, x1] оценки
||R3(p)(x)||[x0 , x1 ] ≤ Kph2 – p||f ″(x)||[x0 , x1 ] ,
p = 0, 1 – порядок производной: при р = 0 получаем погрешность функции, при р = 1 – погрешность производной, где K0 = 1/16, K1 = 0,2515.
Вторая производная многочлена 3(x) не аппроксимирует вторую производную функции f(x). Можно только показать, что
|| 3″(x)||[x0 , x1 ] ≤ 5/3 ||f ″(x)||[x0 , x1 ] .
Если функция f(x) C(4)[x0, x1], то аппроксимируются и вторые производные. Оценки имеют вид:
||R3(p)(x)||[x0 , x1 ] ≤ Kph4 – p||f IV(x)||[x0 , x1 ] , p = 0, 1, 2,
где K0 = 1/384, K1 = 
 3/ 216 ; K2 = 1/12.
3/ 216 ; K2 = 1/12.
18
Привлекают внимание очень малые значения K0 и K1. Сравнивая оценку из табл. 2.1 для эрмитовой кубической интерполяции при p = 0 с оценкой кубической интерполяции, видим, что здесь коэффициент K0 меньше K01 в 9 раз.
Используя большое число соседних точек и аппроксимируя истинную кривую более сложной линией, можно уточнить полученный результат.
Существуют методы нахождения единственного многочлена n-ой степени Pn(x), аппроксимирующего функцию f(x) кривой, проходящей через все n + 1 заданные в таблице точки (xi, yi), где i = 0, 1, ... , n. Многочлен удовлетворяет условиям: Pn(xi) = yi при i = 0, 1, ... ,n.
Методы отыскания такого многочлена делятся на три группы [2]: методы Лагранжа, разностные методы и итерационные методы.
2.6. МЕТОД РАЗДЕЛЁННЫХ РАЗНОСТЕЙ
Существует множество разностных методов интерполяции, однако наиболее распространён метод Ньютона для интерполирования вперёд, известный также как метод Ньютона-Грегори. Интерполяционный многочлен для этого имеет вид [1]:
Pn(x) = c0 + c1(x – x0) + c2(x – x0)(x – x1) + ... + cn(x – x0)(x – x1) ... (x – xn – 1).
Коэффициенты сj находят из уравнений Pn(x) = yi при i = 0, 1, ... , n, позволяющих записать систему:
Pn(x = x0) = c0 + c10 + c20(x0 – x1) + ... +cn0(x0 – x1) ... (x0 – xn – 1);
Pn(x = x1) = c0 + c1(x1 – x0) + c2(x1 – x0)0 + ... +cn(x1 – x0)0... (x1 – xn – 1);
.. .
Pn(x = xn) = c0 + c1(xn – x0) + c2(xn – x0)(xn – x1) + ... + + cn(xn – x0)(xn – x1) ... (xn – xn – 1).
Отсюда:
c0 = y0, x = x0;
c0 + c1 (x1 – x0) = y1, x = x1, (x1 – x0) = h;
c0 + c1 (x2 – x0) + c2 (x2 – x0)(x2 – x1) = y2, x = x2, (x2 – x1) = h, (x2 – x0) = 2h;
.. .
c0 + ... +cn (xn – x0) (xn – x1) ... (xn – xn-1) = yn, x = xn, xn – x0 = nh, xn – x1 = (n – 1)h,…, xn – xn – 1 = h.
Эта линейная система уравнений с треугольной матрицей, и определение с её помощью значений cj не вызывает затруднений. Однако сущест-
19
вует ещё более простой способ определения cj, основанный на применении правых конечных разностей. Если значения x заданы через равные промежутки xi + 1 – xi = h, то в общем случае xi = x0 + ih, где i = 1, 2, ... , n. Последнее выражение позволяет привести решаемые уравнения к виду:
y0 = c0;
y1 = c0 + c1h;
y2 = c0 + c12h + 2h2c2;
.. .
yi = c0 + c1ih + c2ih[(i – 1)h] + ... +ci (i!)hi,
откуда для коэффициентов получаем:
c0 = y0;
c1 = (y1 – c0)/h = (y1 – y0)/h = y0/h .
y0 называется первой правой разностью. Продолжая вычисления, находим:
c2 = (y2 – c0 – c12h)/2h2 = [(y2 – y1) – (y1 – y0)]/2h2 = [ ( y0)]/2h2= 2y0/2h2,
где 2y0 – вторая правая разность, представляющая собой разность разностей. Коэффициент cj можно представить в виде:
cj = jy0/(j!)h j.
В общем случае разности более высоких порядков для функции y = f(x) в интервале x0 ≤ x ≤ xn определяются выражением:
jyi = j – 1yi + 1 – j – 1yi,
где i = 0, 1, ... , n – j. Часто их сводят в таблицы, где разности порядка n выражены через разности порядка n – 1 (табл. 2.2).
R(x) = |f(x) – Ln(x)| ≤ Mn + 1 hn + 1/(n + 1)! q(q – 1)(q – 2) … (q – n);
|
|
Mn + 1 = max|f n + 1(x)|; |
q = (x – x0)/h. |
|
||||||
Интерполяция вперед: |
|
|
|
|
|
|
|
|
||
|
|
|
2 y q(q −1) |
|
3 y q(q −1)(q − 2) |
|
||||
Pn (x) = y0 |
+ y0 q + |
0 |
|
|
|
+ |
0 |
|
+ ... |
|
2! |
|
|
3! |
|
||||||
|
|
|
|
|
|
|
|
|||
|
i y q(q −1)...(q − i +1) |
|
n y q(q −1)...(q − n +1) |
|
||||||
... + |
0 |
|
|
|
+ |
|
0 |
|
|
. |
|
i! |
|
|
|
|
n! |
||||
|
|
|
|
|
|
|
|
|||

20
Таблица 2.2
Правые разности
|
xi |
yi |
|
|
y = y |
|
|
– y |
|
|
|
|
|
2yi = |
|
|
|
|
|
|
|
|
3yi = |
|
|
|
|
|
|
4yi = |
|
|
|
|
|
|
|
5yi = |
|
|
|
||||||||
|
|
|
i + 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
4 |
|
|
|||||||||||
|
|
|
|
|
|
i |
|
|
|
= yi + 1 – yi |
|
= |
yi + 1 – |
|
= |
yi + 1 – |
yi |
= |
yi+ 1 – |
yi |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x0 |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4y |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
x3 |
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4y1 |
|
|
|
|
|
|
|
… |
|
|
|
||||
|
|
|
|
|
|
|
|
y |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y |
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y4 |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x5 |
y5 |
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интерполяция назад: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 yn − 2 q(q +1) |
|
3 yn − 3q(q +1)(q + 2) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Pn (x) = yn + |
yn −1q + |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ... |
|
|
|
|
||||||||||||
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
i yn − i q(q + 1)...(q + i −1) |
|
n y q(q +1)...(q + n −1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
... + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
i! |
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
f '( x) ≈ |
|
y |
; |
|
f "(x) ≈ |
|
|
2 y |
;...; |
|
f (i ) (x) ≈ |
|
(i ) y |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
hi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Пример [3]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Даны следующие точки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x |
|
2,0 |
|
|
|
2,1 |
|
2,2 |
|
|
|
|
|
2,3 |
|
|
|
2,4 |
|
|
|
2,5 |
|
|
|
|
2,6 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
y |
|
|
0,0540 |
|
|
0,0440 |
|
0,0355 |
|
|
|
|
|
0,0283 |
|
0,0244 |
|
|
|
0,175 |
|
|
0,0136 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
Необходимо найти y(2,05). Используем для интерполяции только три |
||||||||||||||||||||||||||||||||||||||||||||||
первые точки, а остальные используем для оценки погрешности. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Следовательно, |
|
n = 2, |
относительное |
|
значение |
|
|
|
аргумента |
|||||||||||||||||||||||||||||||||||||
q = (x – x0)/h (h = 0,1, что видно из исходных данных) будет равно q = 0,5. Воспользуемся первой интерполяционной формулой Ньютона для безразмерной переменной q, для чего предварительно составим таблицу конечных разностей (табл. 2.3).
