Малышев Вычислительная математика EQ3

71

ные формулы Гаусса, т. к. они более эффективны и лучше приспособлены для компьютерных вычислений.

Пример [3].

Рассмотрим вычисление интеграла из предыдущего примера. Выберем k = 4.

2) в этом случае разобьем интервал на четыре участка (n = 4) c h = 0,25, применим для каждого интервала формулу с k = 4, сложим результаты и получим I ≈ 0,78539817.

6.5. ИНТЕГРИРОВАНИЕ ПО МЕТОДУ РОМБЕРГА

Из всех формул Ньютона-Котеса метод трапеций является наиболее простым, однако он не даёт достаточной степени точности. Метод Ромберга получил широкое распространение, поскольку сочетает в себе простоту метода трапеций с высокой точностью вычисления [1]. Он состоит в применении экстраполяционного метода Ричардсона для улучшения результатов, полученных с помощью метода трапеций. Для интегрирования по методу Ромберга вспомним метод трапеций:

где h = (b – a)/m и xj = a + jh. Известно, что погрешность усечения уменьшается с увеличением числа шагов m. Один из способов повышения систематического повышения m состоит в использовании прогрессии вида:

m = 2k – 1, k = 1, 2, ... , n,

где n – целое положительное число. Шаг h для такой прогрессии уменьшается как:

hk = b – a/2k – 1, k = 1, 2, ..., n.

h1 = b – a/21 – 1 = b – a/1, отсюда m = 1

h2 = b – a/22 – 1= b – a/2, m = 2 h3 = b – a/23 – 1= b – a/4, m = 4

Удобно обозначить Rk,1 приближённое значение интеграла, тогда:

72

Можно показать, что эта последовательность записывается в общем виде как:

для каждого k = 2, 3, ... , n. Это выражение можно использовать для ускорения процесса вычисления каждого Rk,1. В то время как k увеличивается, точность Rk,1 также увеличивается, однако сходимость к точному значению интеграла очень медленная. Для ускорения процесса сходимости используют экстраполяционную формулу Ричардсона:

Rij = [22(j – 1) Ri,j – 1 – Ri – 1,j – 1]/(22(j – 1) – 1).

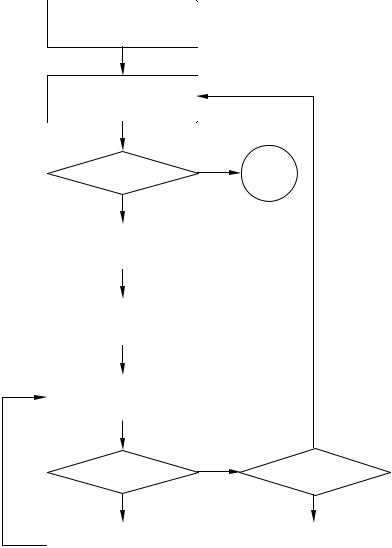
для каждого i = 2, 3, ... , n; j = 1, 2, ... ,i, где экстраполированное значение, отвечающее большему индексу j, соответствует более старшему порядку в формулах Ньютона-Котеса (рис. 6.3).

Результат аппроксимаций может быть записан в виде треугольной матрицы:

R1,1

R2,1 R2,2

R3,1 R3,2 R3,3

R4,1 R4,2 R4,3 R4,4

.. .

Rn,1 Rn,2 ... Rn,n

Диагональные элементы сходятся к точному значению интеграла быстрее, чем Rn,1. Обычно процедура применения итерационной схемы метода Ромберга заключается в последовательном нахождении элементов в строчках до тех пор, пока для некоторого n разность между Rn,n и Rn – 1,n – 1 меньше некоторой наперёд заданной погрешности.

6.6. КВАДРАТУРНЫЕ ФОРМУЛЫ ГАУССА

Все формулы интегрирования Ньютона-Котеса используют равноотстоящие координаты абсцисс. Если это ограничение снято, расстояние между точками можно выбрать таким образом, чтобы понизить погрешность аппроксимации.

В выражении:

73

wi и xi взяты неизвестными, подлежащими определению. Таким образом, полное число неизвестных параметров равно 2(n + 1). Полином степени 2n + 1 для своего однозначного определения требует задания 2n + 2 узлов.

h = b – a; i = 1; j = 1

Вычислить R1,1

i = i + 1

Рис. 6.3. Алгоритм интегрирования по формулам Ньютона-Котеса

Будем аппроксимировать интеграл, используя полином степени 2n + 1, и потребуем, чтобы для всех полиномов со степенями, равными или меньшими этого значения, погрешности аппроксимации были равны нулю. Это условие даст 2n + 2 уравнений для 2n + 2 неизвестных. В общем случае конечные уравнения окажутся линейными относительно wi, но нелинейными относительно xi. Если пределы интегрирования составляют [–1, 1], значениями xi станут n + 1 корней полинома Лежандра Pn + 1(x) = 0. После того как найдены xi величины wi могут быть найдены методами решения линейных систем. Рассмотрим случай с n = 1. Требование, чтобы равенство

удовлетворялось для всех полиномов степени 2n + 1 и меньше, означает, что для f(x) = 1, x, x2 и x3 равенство должно строго выполняться. Из этого получаем следующие уравнения:

1

w0 + w1 = ∫ dx = 2 ;

−1

1

w0 x0 + w1 x1 = ∫ xdx = 0 ;

w0 x03 + w1 x13 = ∫ x3dx = 0 .

−1

Система четырёх уравнений для четырёх неизвестных может быть решена даже для нелинейных уравнений. Чтобы избежать трудностей, связанных с нелинейностью, возьмём полином Лежандра в виде:

P2(x) = –1 + 3x2.

Преимуществом подобной схемы является то, что корни полиномов Лежандра хорошо известны и табулированы в литературе.

Полином второй степени имеет корни x1 = −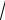3 / 3 и x2 = −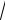3 / 3 . Используя эти значения и два любых уравнения из выше приведённых, получим, что w0 = 1 и w1=1. Тогда интеграл записывается в виде:

Ограничение, связанное с необходимостью выбора промежутка интегрирования от –1 до 1 не настолько затруднительно. Очевидно, что замена переменных z = 2x – (a + b)/(b – a) преобразует интеграл к требуемому виду:

Таким образом, применение метода квадратур Гаусса с n = 2 для вычисления интеграла даёт:

77

поляция, аппроксимация, сглаживание для двумерного и многомерного пространства. Пособие содержит основные вопросы, связанные с численными методами вычисления производных и интегралов.

Весь материал снабжен рекомендациями по выбору методов и примерами вычислений.

В пособие не вошли материалы, посвященные решению систем уравнений и дифференциальных уравнений.

Студенты, изучившие это пособие, должны хорошо ориентироваться в современных методах обработки данных.

СПИСОК ЛИТЕРАТУРЫ

1. Шуп Т. Прикладные численные методы в физике и технике: Пер. с англ. С. Ю. Славянова/под ред. С. П. Меркурьева. – М.: Высш. шк., 1990. –

255с.

2.Завьялов Ю. С., Леус В. А., Скороспелов В. А. Сплайны в инженерной геометрии - М.: Машиностроение, 1985. – 224 с.

3.Васильков Ю. В., Васильков Н. Н. Компьютерные технологии вычислений в математическом моделировании – М.: Финансы и статистика,

2002.

4.Стечкин С. Б., Субботин Ю. Н. Сплайны в вычислительной мате-

матике. – М.: Наука, 1976. – 248 с.

5.Малышев Р. А. Автоматизация контроля химического состава, структуры и свойств чугуна на основе создания многофункционального комплекса вычислительных средств. Диссертация на соискание учёной степени кандидата технических наук. Рыбинск: РГАТА, 2001.