Малышев Вычислительная математика EQ3

31

В общем виде кусочно-полиномиальные функции представляются следующим образом:

P(x) = Pi (x), xi ≤ x ≤ xi + 1, i = 0, 1, ... , k – 1 – полиномы для каждого отрезка;

Pi(j)(xi) = Pi + 1(j)(xi), j = 0, 1, ... , i – 1, – непрерывность в точках соприкосновения (одинаковость производных соседних полиномов в узлах),

где i = 1, ... , k – 1.

Точки x1, ... xk – 1, которые делят сегмент [a, b] на k подсегментов, называются точками склеивания, а точки воспроизводимой кривой, соответствующие этим значениям x – узлами. Для удобства принимают x0 = a,

xk = b.

Функция Sn,ν (x) называется сплайном степени n класса Cm (0≤ m ≤ n; ν = n – m) с m непрерывными производными и с узлами на сетке : a = x1 < < ... < xi < ... < xN = b, если:

а) на каждом отрезке [xi, xi + 1], i = 1, ... , N – 1, функция Sn,ν(x) является многочленом степени n, т. е.

n

Sn,ν (x) = Pni (x) = ∑ aki (x − xi )k =a0 + a1 (x − xi ) + a2 (x − xi )2 +....

k =0

для x [xi, xi + 1];

б) Sn,ν(x) Cm [a, b].

Производные сплайна Sn,ν(p)(x) порядка выше m и до n включительно, вообще говоря, имеют конечные разрывы в точках xi, p = 2, ... , N – 1 – порядок производной, n – степень полинома (сплайна). Индекс ν = n – m указывает на число таких производных. Число ν часто называют дефектом сплайна.

3.3.1. Пространство сплайнов

Множество сплайнов, удовлетворяющих определению, обозначается через Sn,ν( ). Каждое звено сплайна зависит от n + 1 коэффициентов, определяющих его многочлен. Общее число коэффициентов (n + 1)(N – 1). Но в точках xi, i = 2, ... , N – 1 должны выполнятся условия непрерывности первых m = n – ν производных сплайна, которые дают (n – ν + 1) Х (N – 2) линейных уравнений для коэффициентов api. Таким образом, остается число независимых коэффициентов

= (n + 1)(N – 1) – (n + 1)(N – 2) + ν (N – 2) = n + 1 + ν (N – 2). Это есть раз-

мерность пространства сплайнов Sn,ν( ).

32

Задачи аппроксимации сплайнами – это, с одной стороны, те же задачи, что и для многочленов, а с другой – специфические проблемы, рассматриваемые только в теории сплайнов.

К первым относится задача интерполяции. Для сплайнов нечётных степеней, например первой и третьей, характерна схема, при которой узлы интерполяции и узлы сплайна совпадают. В случае чётных степеней, например параболических сплайнов, узлы не совпадают, а чередуются между собой.

Погрешность аппроксимации сплайнами характеризуется так же, как и в случае многочленов, нормой остаточного члена ||Rn,ν(x)|| = ||Sn,ν(x) –

– f(x)||. Она снова зависит от того, к какому классу: Cm[a, b] или C(m)[a, b] принадлежит функция f(x), и от шагов hi сетки .

Уменьшение шага ведёт к увеличению числа узлов. В случае многочленов это связано с возрастанием их степени. Степень же сплайна не изменяется.

При переходе от аппроксимации многочленами к аппроксимации сплайнами преследуют две цели [4]. Первая, это улучшение качества приближения: при одинаковых вычислительных затратах абсолютные погрешности аппроксимации сплайнами меньше, чем погрешности аппроксимации многочленами, а при одинаковых погрешностях уменьшается объём вычислений. Сплайны позволяют избежать осцилляций. Для сходимости аппроксимации к аппроксимируемой функции предъявляются более слабые требования, чем в случае многочленов. Вторая цель – резкое уменьшение вычислительных трудностей как при построении алгоритмов решения задач, так и при дальнейшей работе с аппроксимантами, которые на каждом звене представляют собой многочлены невысоких степеней или иные элементарные функции. С этой точки зрения наиболее простыми оказываются задачи локальной аппроксимации. В таких случаях решения выписываются обычно в явном виде. Нелокальные задачи сводятся к решению систем линейных уравнений размерности порядка N с разреженными (ленточными) матрицами, для которых существуют эффективные алгоритмы. В этом заключается одно из преимуществ сплайнов перед многочленами высоких степеней, где матрицы заполненные [4].

При работе со сплайнами можно использовать либо кусочномногочленное представление, либо представление через базисные функции. В первом случае достигается наибольшая экономия в числе арифметических операций, но зато приходится хранить большой объём информации о многочленах – (n + 1)(N – 1) чисел. Во втором случае достаточно хранить dn,ν = n + 1 + ν (N – 2) коэффициентов сплайна, но при этом увели-

33

чивается число арифметических операций. Следует предупредить, что не все базисы пригодны для организации вычислений. Большей частью их применение приводит к быстрому накоплению погрешностей округления. В частности, при использовании усечённых степенных функций затруднения возникают при вычислении второй суммы при больших N. От этого недостатка свободен лишь базис, состоящий из функций с конечными носителями (отличных от нуля на конечном отрезке), так называемых В-сплайнов.

3.3.2. Сплайны первой степени

Интерполяция. Сплайны первой степени S1(x) класса C на сетке

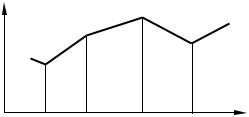
– это кусочно-линейные функции. (Здесь и далее второй индекс ν сплайна, если он равен единице, опускается). Пусть в узлах сетки заданы значения функции fi = f(xi). Интерполяционный сплайн S1(x) определяется условиями S1(xi) = fi, i = 1, …, N. Геометрически он представляет собой ломаную, проходящую через точки (xi, fi) (рис. 3.3). Между соседними узлами реализуется линейная интерполяция. Согласно [1, 4] при x [xi, xi + 1] сплайн будет иметь вид:

S1 ( x) = (1 − u) fi + ufi +1 ; u = (x − xi ) / hi .

S1(x)

xi – 1 xi xi + 1 xi + 2 x

Рис. 3.3. Сплайн первой степени

Если в исходные данные fi внести возмущения δfi ≤ δ, то сплайн изменится в пределах δ. Возмущение его производной оценивается значением δ/hi и растет с уменьшением hi.

Погрешность интерполяции. Пусть f(x) C(2)[a, b], тогда

34

Интерполяция с заданной точностью. На практике обычно требуется осуществить интерполяцию с некоторой заданной точностью. Эта задача решается путем выбора сетки на отрезке [a, b] с учетом свойств интерполируемой функции. Точность интерполяции определяется гладкостью функции внутри отрезков [xi, xi + 1]. Поэтому точки, в которых функция имеет особенности, например, разрывы производных, следует включить в число узлов интерполяции.

Оценка при p = 0 дает возможность определить максимальный шаг

и требуемая точность обеспечивается, например, на равномерной сетке с шагом h. При этом число узлов, как правило, будет очень завышенным.

С помощью оценки при p = 0 можно строить более экономичные по

то задача будет решена с числом узлов, вообще говоря, меньшим, чем при равномерном разбиении.

Пусть, например, функция f ′′( x) монотонно убывает на [a, b]. Если

то xi + 1 = b. Начиная этот процесс от левого конца отрезка [a, b], последовательно находим все узлы сетки. Если f ′′( x) монотонно возрастает, то

построение следует начинать с правого конца отрезка [a, b]. Алгоритм можно применять, если функция f ′′( x) кусочно-монотонна. Алгоритм выбора узлов сплайна, при котором не требуется выделять участки монотонности функции f ′′( x) , будет изложен ниже.

Аппроксимация сплайнами первой степени. Аналогом асимптотиче-

ски наилучшего равномерного приближения многочленом первой степени является следующая аппроксимация сплайном:

35

Производные можно заменить конечно-разностными аппроксимациями (см. п. 5.2 – 5.4). При этом будет внесена погрешность порядка Θ(H2). Отсюда ясно, что главный (первый) член погрешности аппроксимации не изменится.

3.3.3. Кубические сплайны

Кубический сплайн склеивается из полиномов третьей степени, которые для i-го участка записываются так [1 – 5]:

y = ai (x – xi)3 + bi (x – xi)2 + ci (x – xi) + di.

Для всего интервала будет соответственно n кубических полиномов, отличающихся коэффициентами ai, bi, ci, di. Чаще всего узлы при сплайновой интерполяции располагают равномерно, т. е. xi + 1 – xi = const = h (хотя это необязательно).

Необходимо найти четыре коэффициента при условии прохождения каждого полинома через две точки (xi, yi) и (xi + 1, yi + 1), следствием чего являются следующие очевидные уравнения:

Найти все коэффициенты из этих уравнений нельзя, т. к. условий меньше, чем искомых параметров. Поэтому указанные условия дополняют условиями гладкости функции (т. е. непрерывности первой производной) и гладкости первой производной (т. е. непрерывности второй производной) в узлах интерполяции. Математически эти условия записываются как равенства соответственно первой и второй производных в конце i-го и в начале (i + l)-гo участков.

Так как

y′ = 3ai (x − xi )2 + 2bi ( x − xi ) + ci и y′′ = 6ai (x − xi ) + 2bi ,

Получилась система линейных уравнений (для всех участков), содержащая 4n – 2 уравнения с 4n неизвестными (неизвестные a1, a2, . . ., an, b1, . . ., dn – коэффициенты сплайнов). Для решения системы добавляют два граничных условия одного из следующих видов (чаще применяют 1):

Совместное решение 4n уравнений позволяет найти все 4n коэффициента.

Для восстановления производных можно продифференцировать на каждом участке соответствующий кубический полином. В случае необходимости определения производных в узлах существуют специальные приемы, сводящие определение производных к решению более простой системы уравнений относительно искомых производных второго или первого порядка. К важным достоинствам интерполяции кубическими сплайнами относится получение функции, имеющей минимальную возможную кривизну. К недостаткам сплайновой интерполяции относится необходимость получения сравнительно большого числа параметров. Вычислительный пример рассматривать не будем, что связано с большим объемом вычислений, которые нецелесообразно проводить вручную.

3.3.4. Эрмитовы кубические сплайны

Интерполяция

В узлах сетки заданы значения функции и ее производной fi = f(xi), fi′ = f ′(xi), i = 1, …, N. Требуется найти кубический сплайн S3,2(x) такой, что

S3,2(xi) = fi; S′3,2(xi) = fi′, i = 1, …, N.

Это эрмитов кубический сплайн [2]. Его первая производная непрерывна, а вторая и третья в общем случае разрывны в узлах сетки. График представляет собой гладкую линию.

37

На отрезке [xi, xi + 1] реализуется эрмитова интерполяция кубическим многочленом. Звено сплайна имеет вид

где K0 = 1/384; K1 = 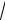3 / 216 ; K2= 1/12.

Эти оценки остаются справедливыми и для функций с кусочнонепрерывными вторыми и третьими производными, если точки их разрыва включаются в число узлов интерполяции. В инженерной практике к такому классу относятся часто используемые гладкие кусочно-аналитические функции.

Из полученных формул получаются оценки, справедливые на всем

отрезке [a, b], заменой hi на H и ... на ... .

xi , xi +1

Интерполяция с заданной точностью. Задача интерполяции с точ-

ностью

R( x) = S3, 2 ( x) − f ( x) ≤ ε, x [a, b]

решается двояко. Шаги равномерной сетки для функций f(x) C2 [a, b] можно определить:

h≤ 4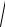ε / f ′′( x) .

Ашаги для функций f(x) C4 [a, b]:

h ≤ 4384ε / f IV ( x) .

38

Для построения неравномерных сеток при интерполяции функций f(x) C(2) [a, b] можно использовать алгоритм, приведенный в п. 4. Для функций f(x) C(4) [a, b] в этом алгоритме нужно всюду заменить f ″(x) на f IV(x).

Ниже рассмотрен другой алгоритм построения неравномерной сетки, не требующий вычисления производных f ″(x) или f IV(x). Он достаточно трудоемок, но зато позволяет получать сетки с минимальным числом узлов.

На отрезке [a, b] возьмем множество точек (контрольных) τi = a + jδx, j = 0, …, и предположим, что остаточный член интерполяции в них удовлетворяет условию

R(τ j ) = S3, 2 (τ j ) − f (τ j ) ≤ ε1 < ε .

Выясним, когда на основании этого можно утверждать, что заданная точность обеспечивается на всем отрезке [a, b].

Построим сплайн первой степени S1(x), интерполирующий функцию R(x) по значениям R(τj). Поскольку R(τ j ) ≤ ε1 , то S1 ( x) ≤ ε1 на всем отрезке [a, b]. Отсюда ясно, что достаточно добиться выполнения неравенства

δR(x) = S1 (x) − R( x) ≤ ε − ε1 ,

и тогда условие заданной точности будет выполнено.

Согласно формуле погрешности интерполяции сплайна первой сте-

пени

δR( x) ≤ 0,125(δx)2 R′′( x) .

Если функция f(x) C2[a, b], то учитываем, что

δR(x) ≤ 3−1 (δx)2 f ′′(x) .

На шаги δx налагаем ограничение

δx ≤ 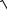3(ε − ε1 ) / f ′′(x) .

При этом ограничении исходные неравенства будут выполнены. Рассмотрим узловые моменты алгоритма. Ввиду локальности эрми-

това сплайна задача состоит в последовательном определении по возмож-

39

ности максимальных размеров каждого шага сетки . Предполагается, что известна оценка f ′′(x) ≤ A . Зададим значение ε1 и по приведенным выше

формулам определим максимально допустимый шаг δx и шаг h равномерной сетки, обеспечивающей точность ε интерполяции: δx =

h = 4ε / A .

Пусть найден узел xi – 1.Узел xi находим путем последовательных

1. ε < ε1. Экстраполируем звено сплайна вправо и вычисляем его

Нетрудно убедиться, что процесс последовательного приближения сходится, т. к. допустимый отрезок α( k ) ,β(k ) на каждом шаге уменьшает-

ся, и как только он становится меньшим δx , можно считать, что узел xi определен.

40

Основные вычислительные затраты этого алгоритма приходятся на

значение A и как выбрано ε1. Очевидно, что большему шагу δx соответствует меньшее значение ε1, т. е. уменьшение числа контрольных точек возможно только за счет уменьшения допустимого уклонения S3,2(x) от f(x) в этих точках. На практике рекомендуется принимать значения ε1 = 0,9 ε. В этом случае δx = и общее число контрольных точек m = (b − a) / δx . Отметим, что конечный результат практически не зависит

δR( x) ≤ 96−1 (δx)2 h2 f IV (x) ≤ (δx)2 ε f IV (x) / 24 .

Чтобы выполнялось условие, следует положить

δx ≤ 424(ε − ε1 )2 / ε f IV ( x) .

Для применения алгоритма нужно знать оценку f IV ( x) ≤ A.

3.3.5. Аппроксимация с помощью сплайна

Сплайны лишь недавно стали использовать в вычислительной математике. Однако в машиностроительном черчении они фактически применяются уже давно, т. к. сплайн – это в переводе не что иное, как «гибкая линейка», которую деформируют так, чтобы по ней можно было провести кривую через заданные точки (xi, уi). Сплайн (или сплайн- функции) – функция с кусочной структурой и повторяющимся на каждом звене (отрезке) строением, но с различными значениями параметров.

Кубический сплайн – это группа сопряженных кубических многочленов, в местах сопряжения которых первая и вторая производные непрерывны. Чтобы построить кубический сплайн, необходимо задать коэффициенты, которые единственным образом определяют кубический многочлен в промежутке между данными точками. Например, в случае, представленном на рис. 3.4, необходимо задать все кубические функции q1(х),

q2(х), . . ., qm(х).