Малышев Вычислительная математика EQ3
.pdf
51
ям характеристик соответствующих точек, по теореме Пифагора найдём сторону С*В*
C*B*= 
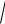C*B'2 + B*B'2 .
Аналогичным образом находятся стороны А*В* и А*С*. Следует отметить также, что стороны С*В*, А*В* и А*С* можно найти по координатам точек х1, х2 и Р, используя формулу для вычисления расстояния S между точками. Таким образом, нашли координаты двух точек А*(0, 0) и В*(0, SА*В*), осталось найти координаты точки С*. По трём сторонам треугольника можно найти его площадь или по теореме синусов или косинусов найти углы треугольника С*В*А*, а затем по полученным данным вычислить значение С*К* – первой координаты точки С* (С* К* – перпендикуляр из точки С* на ось 0Y, высота С*В*А*). Из прямоугольного треугольника С*А*К* найдём сторону А*К* – вторую координату точки С*.
В итоге решение задачи перехода на другие координаты в трёхмерном пространстве оказалось не сложным.
Рассмотрим другой подход для решения задачи о принадлежности точек, лежащих на плоскости, прямой.
Подойдём к решению этой задачи с другой стороны. Пусть точки, по которым необходимо построить плоскость, принадлежат прямой. Тогда получаем прямую А*С* (рис. 4.3).
А* |
B* C* |
|
А* |
|
|
|
C* |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B*
Рис. 4.3. Принадлежность точек прямой
Пусть точка В* лежит между точек А* и С*. Из рис. 4.3 видно, что отрезок А*С* больше отрезков А*В* и В*С* и А*С* = А*В* + В*С*, когда все точки лежат на прямой. А*С* < А*В* + В*С*, если точка В* не лежит на прямой А*С*. Таким образом, если все точки лежат на прямой, то длина максимального отрезка равна сумме длин всех остальных отрезков. Если точки не лежат на одной прямой, то последнее утверждение – не верно.
Таким образом, задача о принадлежности точек, лежащих на плоскости, прямой сводится к нахождению расстояния между двух максимально удалённых точек и сумме расстояний между остальными точками. Для
52
расчёта расстояний между точками следует использовать приведённую выше формулу [5].
По-другому задачу о принадлежности точек, лежащих на плоскости, прямой можно решить при построении плоскости алгебраическим методом.
Уравнение плоскости имеет вид:
a1x + a2 y + a3P = const.
Таким образом, для построения плоскости Ψ необходимо задание трёх точек P(x, y, P). После деления обоих частей на значение константы получается система уравнений вида:
b1x1 + b2y1 + b3P1 = 1; b1x2 + b2y2 + b3P2 = 1; b1x3 + b2y3 + b3P3 = 1.
Перейдём к матричному представлению системы:
x1x2x3
y |
|
P |
|
b |
|
|
1 |
|
1 |
1 |
|
1 |
|
|
1 |
|
|
y |
2 |
P |
|
b |
|
= |
или XB = 1. |
|
|
2 |
|
2 |
|
|
|
|
|
y |
|
P |
|
b |
|
|
1 |
|
3 |
3 |
|
3 |
|
|
|
|
|
Данная система имеет однозначное решение, когда уравнения, составляющие систему линейно-независимы, т. е. одно уравнение нельзя представить через линейную комбинацию других (определитель матрицы характеристик не равен нулю: det (X) ≠ 0). В случае, когда точки лежат на одной прямой, система будет линейно-зависимой и det (X) = 0.
4.2. ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ В МНОГОМЕРНОМ ПРОСТРАНСТВЕ
Переходя к многомерному пространству, имеем уравнение гиперплоскости:
a1x1 + a2x2 + …+ an – 1xn – 1 + anxn = const.
Таким образом, для построения гиперплоскости Ψn необходимо задание n многомерных точек P(x1, x2, …, xn).
В связи с этим возникает новый вопрос о нахождении минимального расстояния до многомерной точки. Для нахождения максимально приближенных к искомой точке рекомендуется применять следующую форму-
лу [5]:
53
S = min S j = min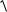 
(x1j − x1j иск. )2 + (x2j − x2j иск. )2 + ... + (xnj − xnj иск. )2 ,
где i = 1, … , n – номер фактора, j = 1, … , k – число значений i-го фактора. Эту формулу можно представить в виде:
|
|
|
n |
|
|
|
S = min S |
j |
= min |
∑ |
(x |
− x |
)2 . |
|
|
|
ij |
ijиск. |
|
|
|
|
|
i =1 |
|
|
|
Та точка, у которой значение Sj минимально, является максимально приближённой.
Рассмотрим решение задачи принадлежности точек, лежащих на гиперплоскости, гиперпрямой. По аналогии с трёхмерным пространством эта задача может быть решена тремя способами.
Для многомерного случая уравнение гиперпрямой имеет вид:
xn – 1* = a1x1* + a2x2* + …+ an – 2xn – 2* + an – 1.
Таким образом, для построения гиперпрямой необходимо решить n – 1 уравнение, т. е. необходимо знать координаты n – 1 многомерной точки на гиперплоскости Ψn. Итак, нам необходимо перейти от координат x1, x2 ,…, xn – 1, xn к координатам x1*, x2* ,…, x*n – 1, xn* на гиперплоскости
Ψn.
Однако при геометрическом методе возникает ряд трудностей. Как привязать ось координат к значениям характеристик?
Как перейти от треугольника к многомерной фигуре, какие свойства фигуры при этом сохранятся?
Что является аналогом прямоугольного треугольника в многомерном пространстве? и др.
При решении этой задачи другими методами этих трудностей не возникает, и поэтому перейдём сразу к ним.
При использовании второго метода задача о принадлежности точек, лежащих на гиперплоскости, гиперпрямой сводится к нахождению расстояния между двух максимально удалённых точек и сумме расстояний между остальными точками. Следует также отметить, что последовательность расположения средних точек должна определяться по минимальному расстоянию между точками. Для расчёта расстояний между точками следует использовать приведённую выше формулу [5].
В итоге можно предположить, что в многомерном пространстве по аналогии с трёхмерным, эти утверждения будут также выполняться, т. е., если многомерные точки принадлежат одной гиперпрямой, то расстояние
54
между двумя максимально удалёнными точками будет равно сумме расстояний между остальными точками.
Однако алгебраческий метод позволяет решить эту задачу на этапе расчёта уравнения гиперплоскости, т. е. без дополнительных вычислений.
Уравнение гиперплоскости имеет вид:
a1x1 + a2x2 + …+ an – 1xn – 1 + an xn = const.
Таким образом, для построения гиперплоскости Ψn необходимо задание n многомерных точек P(x1, x2, …, xn). После деления обоих частей на значение константы получается система уравнений вида:
b1x11 + b2x21 + …+ bn – 1xn – 11 + bn xn1 = 1; b1x12 + b2x22 + …+ bn – 1xn – 12 + bn xn2 = 1;
.. .
b1x1n + b2x2n + …+ bn – 1xn – 1n + bn xnn = 1,
где xij – i-ая координата j-ой n-мерной точки. Перейдём к матричному представлению системы:
x11
x12
x1n
x21 ... |
xn −11 |
x22 ... |
xn −12 |
. . . |
|
x2n ... |
xn −1n |
xn1
xn 2
xnn
|
b |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
b2 |
= |
1 |
|
или XB = 1. |
|
|
... |
|
... |
|||
|
|
|
|
|
|
|
|
bn |
|
1 |
|
||
|
|
|
||||
Данная система имеет однозначное решение, когда уравнения, составляющие систему, линейно-независимы, т. е. одно уравнение нельзя представить через линейную комбинацию других (определитель матрицы характеристик не равен нулю: det (X) ≠ 0). В случае, когда точки лежат на одной гиперпрямой, система будет линейно-зависимой и det (X) = 0.
Исходя из вышесказанного, следует, что алгебраический метод позволяет решить задачу принадлежности точек гиперпрямой на этапе расчёта уравнения гиперплоскости, т. е. без трудностей (геометрический способ) и дополнительных вычислений (по расстояниям между точек).
Итак, наиболее простым и легко реализуемым методом аппроксимации многомерных поверхностей является – построение по n точкам. Однако, как и любая линейная аппроксимация, данный метод обладает низкой точностью, поэтому для повышения точности рекомендуется применять наиболее перспективный в настоящее время методом аппроксимации поверхностей – аппроксимацию многомерными сплайнами [4].
55
4.3. АППРОКСИМАЦИЯ МНОГОМЕРНЫМИ СПЛАЙНАМИ
Сплайны двух и более переменных характеризуются двумя признаками: формой области с её разбиением на подобласти и определением множества сплайнов. В случае двух переменных заданная область прямоугольник Ω = [a, b] X [c, d]. В области Ω вводится сетка линий = x Х s,
причём x: a = x1 < ... < xi < ... < xN = b, |
s: c = s1 < ... < si < ... < sM = d, де- |
||
лящая Ω на прямоугольники Ωij = [xi, xi + 1] X [sj, sj + 1] [4, 5]. |
|||
Функции Sn,ν*(x, s) являются сплайнами степени n класса Cm только |
|||
по переменной x на сетке |
x, а s входит как параметр: |
||
|
|
n |
|
S |
n,ν |
*(x, s) = ∑ ai |
(s)(x − x )k ; |
|
k |
i |
|
|
|
k =0 |
|
(x, s) [xi, xi + 1] X [c, d],
где aki – функции переменной s. Аналогично, если Sn,ν(x, s) есть сплайн по переменной s на сетке s, то
n
Sn,ν *(x, s) =∑ali (x)(s − si )l ;
l =0
(x, s) [a, b] X [sj, sj + 1].
Такие функции называются частичными сплайнами.
Функция Sn,ν(x, s) называется сплайном двух переменных степени n
класса Cm с линиями склейки на сетке |
, если: |
|
|
||
а) на каждой клетке Ωij функция Sn,ν(x, s) является многочленом сте- |
|||||
пени n по каждой из переменных x, s, т. е. |
|
|
|||
|
|
n n |
|
|
|
S |
n,ν |
*(x, s) = ∑ ∑ aij (x − x )k (s − s |
j |
)l , (x, s) Ωij; |
|
|
kl |
i |
|
||
k = 0 l = 0
б) Sn,ν(x, s) Cm, m [Ω].
Погрешность аппроксимации в этом случае характеризуется нормой остаточного члена ||Rn,ν(x, s)|| = ||Sn,ν(x, s) – f(x, s)|| в области Ω. Она зависит от того, к какому классу: Cm [Ω] или C(m) [Ω] принадлежит функция f(x, s),
иот шагов по обеим переменным x, s.
Вслучае n-мерного пространства рассмотрим аппроксимацию с помощью n-мерных сплайнов. Пусть m, x, a, b – точки n-мерного евклидова пространства.
m = (m1, m2,…, mn) – степень многочленов по параметрам xi; x = (x1, x2,…, xn) – аргументы;
a = (a1, a2,…, an) – нижние границы значений параметров xi;
56
b = (b1, b2,…, bn) – верхние границы значений параметров xi; ai ≤ xi ≤ bi, где i = 1, …, n.
Обозначим – множество точек x (a ≤ x ≤ b); введём сетку |
Ni: |
|||||||
|
|
ai = xi(0) < xi(1) < … < xi(Ni) = bi , |
|
|
||||
где i = 1, …, n, Ni – число значений параметра xi; |
N = ( N1, |
N2, …, Nn). |
||||||
При фиксированном m обозначим Pm совокупность алгебраических |
||||||||
многочленов от x, степень по xi которых не превосходит mi. |
|
|
||||||
Пусть j = (j1, j2, …, |
jn), где |
ji – целые |
числа (j-ый |
интервал), |
||||
0 ≤ ji ≤ Ni – 1, i = 1, …, n; |
|
|
|
|
|
|
||
j – совокупность точек x = (x1, x2, …, xn), удовлетворяющих нера- |
||||||||
венствам xi(ji) ≤ xi ≤ xi(ji + 1), i = 1, …, n. |
|
|
|
|
||||
Введём дополнительные числа: |
|
|
|
|
||||
νi(ji) |
= (xi(ji – 1) |
+ xi(ji))/2, |
ji = 1, …, Ni (среднее значение на j – 1 ин- |
|||||
тервале); |
|
|
|
|
|
|
|
|
νi(0) = ai, νi(Ni + 1) = bi, i = 1, …, n (крайние значения) и множества: |
||||||||
Qi – |
точек |
x = (x1, x2, |
…, |
xn), удовлетворяющих |
неравенствам |
|||
νi(ji) ≤ xi ≤ νi(ji + 1), i= 1, …, n. |
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
Точки j и j′ различны, если ∑ |
(j |
− j ')2 >0 [4]. |
|
|
||||
|
|
|
|
i |
i |
|
|
|
|
|
|
i =0 |
|
|
|
|
|
Обозначим через J совокупность различных точек j, координаты ко- |
||||||||
торых удовлетворяют неравенствам 0 ≤ ji ≤ Ni |
– 1, i = 1, …, n; через |
|||||||
I – неравенствам 0 ≤ ji ≤ Ni, i = 1, …, n. Тогда, очевидно, |
|
|
||||||
|
|
= j = Q j |
|
|
|
|||
|
|
|
j J |
|
j I |
|
|
|
Под x(j) будем понимать точку x = (x1(j1), x2(j2), …, xn(jn)), а под m точку m = (m1, m2,…, mn), у которой mi = r, i = 1, …, n.
C(m)( ) – совокупность функций, у которых все частные производные, порядок которых по xi не превосходит mi, i = 1, …, n, m = (m1, m2,…, mn), непрерывны в .
C(m(r))( ) – совокупность функций, у которых все частные производные, порядок которых по xi не превосходит r, i = 1, …, n, непрерывны в .
По определению [4] функция Sm(2)(x) называется интерполяционным n-мерным параболическим сплайном для функции f(x) относительно сетки N, если
а) Sm(2)(x) Pm(2), x Qj (j I);
57
б) Sm(2)(x) C(m(1))( ) (т. е. первые частные производные непрерывны);
в) Sm(2)(x(j)) = f(x(j)), j I,
где Pm(k) – n-мерный многочлен степени k.
Если возникает необходимость подчеркнуть, что Sm(2)(x) интерполирует функцию f(x), то используется обозначение Sm(2)(x, f).
Совокупность сплайнов, удовлетворяющих условиям а) – в), обозначим Sm(2), N. Индукцией по размерности легко показать, что совокупность
сплайнов из Sm(2), N имеет размерность (N1 + 3) (N2 + 3)… (Nn + 3). Число условий в) равно (N1 + 1)(N2 + 1)… (Nn + 1). Чтобы однозначно определить сплайн, необходимо задать ещё соответствующее число краевых условий.
Широкое применение на практике нашли сплайны невысоких степеней, такие как параболические и кубические.
По определению [4] функция Sm(3)(x, f) называется интерполяционным кубическим сплайном для функции f(x) относительно сетки N, если
а) Sm(3)(x, f) Pm(3), x j (j J);
б) Sm(3)(x, f) C(m(2))( );
в) Sm(3)(x, f) = f(x(j)), j I.
Совокупность сплайнов, удовлетворяющих условиям а) – в), обозначим Sm(3), N. Размерность множества Sm(3), N совпадает с размерностью множества Sm(2), N, следовательно, можно рассматривать интерполяционные сплайны с теми же краевыми условиями, что и для параболических многомерных сплайнов.
5. МЕТОДЫ ДИФФЕРЕНЦИРОВАНИЯ
При анализе инженерных и научных данных часто возникает необходимость найти производные функций, наклон кривой или площадь под кривой. Для решения этих задач можно воспользоваться графическим методом, однако, нередко точность таких операций ограничивает пригодность получаемых результатов. По этой причине необходимы численные процедуры дифференцирования и интегрирования.
В случае аппроксимирования производной табулированных значений функции числовые формулы для приближённых производных могут быть получены из разложения в ряд Тейлора или дифференцированием интерполяционных формул или использованием формул конечных разностей. Этот метод состоит в том, чтобы подобрать полином, удовлетворяющий данным точкам, а затем использовать производную полинома в качестве производной табулированных значений. При применении процедуры
58
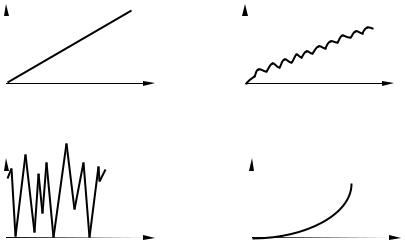
сглаживания сплайном или многочленом такой полином или полиномы в итоге получаются. Рассмотрим два потенциальных источника встречающихся при этом трудностей [1]. Первая трудность проистекает из природы табулированной информации, полученной экспериментальными средствами. В каждом экспериментальном измерении в большей или меньшей степени всегда присутствуют шумы или погрешности эксперимента. Так действительный сигнал, показанный на рис. 5.1, а, в результате измерений в присутствии шума выглядит так, как изображено на рис. 5.1, б. Если эти данные продифференцировать, влияние погрешности существенно возрастёт (рис. 5.1, в). С другой стороны, если данные с шумом проинтегрировать (рис. 5.1, г), то влияние ошибки уменьшается. Таким образом, численное интегрирование представляется гораздо более устойчивой процедурой, чем численное дифференцирование.
f(x) |
|
fизм(x) |
|
|
|
|
|
|
x
a)
f ′(x) |
∫f(x) |
x
в)
x
б)
x
г)
Рис. 5.1. Исследуемые кривые:
а) истинный сигнал; б) измеренный сигнал; в) производная измеренного сигнала; г) интеграл измеренного сигнала
Вторая трудность, связанная с численным дифференцированием, проиллюстрирована на рис. 5.2. Даже если интерполяционный многочлен сможет адекватно описать табулированную функцию, его производные высоких порядков могут совершенно отличатся от таких производных табулированной функции. Это можно увидеть на рис. 5.2, если сравнить наклоны и радиусы кривизны двух кривых.
|
59 |
|
|
|
|
y |
|
f(x) |
|
|
|
|
|
P(x)
x
Рис. 5.2. Производная высокого порядка
5.1. ДИФФЕРЕНЦИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ РАЗНОСТЕЙ
Возьмём интерполяционный многочлен второй степени в таком виде, чтобы он проходил через три соседние точки (x0, y0), (x1, y1) и (x2, y2):
P( x) = |
(x − x1 )(x − x2 ) |
y0 + |
( x − x0 )( x − x2 ) |
+ |
(x − x0 )( x − x1 ) |
||
|
|
y1 |
|
y2 . |
|||
( x0 − x1 ) ( x0 − x2 ) |
|
|
|||||
|
|
( x1 − x0 ) ( x1 − x2 ) |
|
( x2 − x0 )( x2 − x1 ) |
|||
Первая производная этого выражения имеет вид:
P′( x) = |
(2x − x1 − x2 ) |
|
+ |
(2x − x0 |
− x2 ) |
+ |
(2x − x0 |
− x1 ) |
||
|
y0 |
|
|
y1 |
|
|
y2 . |
|||
( x0 − x1 ) ( x0 − x2 ) |
|
|
|
|
||||||
|
|
|
(x1 − x0 ) ( x1 − x2 ) |
|
( x2 − x0 )( x2 − x1 ) |
|||||
Если это выражение вычислить при x = x0, результатом окажется значение первой производной, полученное по левым разностям. Если это выражение вычислить при x = x1, найдём первую производную по центральным разностям. При x = x2 получим производную по правым разностям. Формулы с центральной разностью неприменимы для начальной и для конечных точек в таблице данных.
Для более точных значений левой, центральной и правой разностей при нахождении производных можно использовать аппроксимирующие многочлены старшей степени с более чем тремя узлами. Кроме того, приближенные значения производных более высокого порядка найдены дифференцированием полученных многочленов.
При равностоящих друг от друга значениях x выражения для приближённых вычислений производных упрощаются. Если шаг составляет x1 – x0 = h, приближение правой разностью для производной в точке x0 есть
P′(x) = (–3y0 + 4y1 – y2)/(2h).
Для оценки величины ошибок аппроксимации используем разложение в ряд Тейлора в виде:
60
f(x + ζ) = f(x) + ζ/1! f ′(x) + ζ2/2! f ″(x) + ζ3/3! f ′″(x) + ... .
Если x = x0 и ζ = h (единичный шаг), то f(x0 + h) = y1. Тогда y1 = y0 + hD(y0) + (h2/2)D2(y0) + (h3/6)D3(y0) + ... .
Аналогично, если ζ = 2h, получаем
y2 = y0 + 2hD(y0) + 4(h2/2)D2(y0) +8(h3/6)D3(y0) + ... .
Избавляясь от второй производной в этих уравнениях домножением первого из них на 4, второго на –1 и затем, складывая их, получаем в итоге:
D(y0) = (4y1 – y2 – 3y0)/(2h) + h2y0″′/3.
Найденное второе приближение первой производной совпадает с вычисленным ранее, за исключением слагаемого h2y0′″/3, характеризующего погрешность.
Аналогичная процедура может быть применена для нахождения производной с более высоким приближением для левой, центральной и правой разностей наряду с вычислением соответствующих погрешностей.
Приближённые формулы дифференцирования пятых разностей [1]:
1) y0′
(–3y4 +16y3 – 36y2 + 48y1 – 25y0)/12h левая; (–y2 + 8y1 – 8y–1 + y–2)/12h центральная;
(3y–4 – 16y–3 + 36y–2 – 48y–1 + 25y0)/12h правая;
2) y0″
(11y4 – 56y3 + 114y2 – 104y1 + 35y0)/12h2; (–y2 + 16y1 – 30y0 + 16y–1 – y–2)/12h2;
(11y–4 – 56y–3 + 114y–2 – 104y–1 + 35y0)/12h2;
3) y0′″
(–3y4 + 14y3 – 24y2 + 18y1 – 5y0)/2h3; (y2 – 2y1 +2y–1 – y–2)/2h3;
(3y–4 – 14y–3 + 24y–2 – 18y–1 + 5y0)/2h3.
5.2. КОНЕЧНО-РАЗНОСТНАЯ АППРОКСИМАЦИЯ ПРОИЗВОДНОЙ (ДВУХТОЧЕЧНАЯ СХЕМА)
Дифференцируя формулу линейной интерполяции [2]
L1(x) = (1 – u)fk + ufk + 1