
Малышев Вычислительная математика EQ3
.pdf
21
|
|
|
|
Таблица 2.3 |
|
|
Таблица конечных разностей |
|
|
||
|
|
|
|
|
|
x |
y |
By |
B2y |
B3y |
|
2,0 |
0,0540 |
–0,0100 |
0,0015 |
–0,0002 |
|
|
|
|
|
|
|
2,1 |
440 |
85 |
13 |
0 |
|
|
|
|
|
|
|
2,2 |
355 |
72 |
13 |
3 |
|
|
|
|
|
|
|
2,3 |
283 |
59 |
10 |
10 |
|
|
|
|
|
|
|
2,4 |
224 |
49 |
0 |
|
|
|
|
|
|
|
|
2,5 |
175 |
49 |
|
|
|
|
|
|
|
|
|
2,6 |
136 |
|
|
|
|
Для большей наглядности в таблице опущены нули и знаки, которые показаны лишь в первой строчке каждого столбика.
y(2,05) = 0,0540 + 0,5(–0,01) + 0,5(0,5 – 1) 0,0015/3! = 0,0488125.
Оценим погрешность найденного значения y. Из таблицы находим, что M3 = 0,0010, тогда
R ≤ 0, 001 0, 5(0, 5 −1)(0, 5 − 2) = 0, 0000625 . 3!
Одно из достоинств рассматриваемого метода состоит в том, что он позволяет уточнить результат, используя дополнительные разности, причём нет необходимости начинать вычисления сначала. Поэтому в случае, если неизвестно, сколько членов следует взять, их число можно увеличивать до тех пор, пока их вклад не станет пренебрежимо малым.
Используя другие разности, получим другие интерполяционные схемы, например метод Ньютона для интерполяции назад, методы Гаусса для интерполяции вперед и назад.
2.7. ИТЕРАЦИОННЫЕ МЕТОДЫ ИНТЕРПОЛЯЦИИ
Эти методы основаны на повторном применении простой интерполяционной схемы. Наиболее известным из них является метод Эйткена, сущность которого состоит в повторном применении линейной интерполяции.
Линейная интерполяция между точками (x0, y0) и (xi, yi) осуществляется по формуле [1]:
yi1(x) = (xi – x0)–1[y0(xi – x) – yi (x0 – x)],
22
с помощью которой, задав значение xi, можно составить таблицу функций yi1(x), где i = 1, 2, ... , n. Пользуясь этими функциями, с помощью линейной
интерполяции: yi2(x) = (xi –x1)–1[y11(x)(xi – x) – yi1(x)(x1 – x)], получим новое семейство соотношений. Простой подстановкой можно показать, что вы-
ражение для yi2(x) представляет собой многочлены второй степени, описывающие кривые, проходящие через точки (x0, y0), (x1, y1) и (xi, yi). Получив многочлены yi2 с помощью линейной интерполяции и, используя функции yi2(x), можно записать выражение для многочлена третьей степени: yi3(x) =
= (xi – x2)–1[y22(x)(xi – x) – yi2(x)(x2 – x)], описывающего кривые, проходящие через точки (x0, y0), (x1, y1), (x2, y2) и (xi, yi). Продолжая этот процесс, получим значения yij(x), которые будут стремиться к значению f(x). Хотя в
принципе этот метод позволяет вводить многочлены степени n > 3, обычно стремясь избежать роста ошибок, этого не делают. Следует, однако, отметить, что метод Эйткена не требует, чтобы используемые для интерполяции значения функции были расположены через равные интервалы
(h ≠ const).
Существует множество разностных методов интерполяции [1], однако наиболее распространён метод Ньютона для интерполирования вперёд, известный также как метод Ньютона-Грегори, основанный на применении правых конечных разностей. Одно из достоинств рассматриваемого метода состоит в том, что он позволяет уточнить результат, используя дополнительные разности, причём нет необходимости начинать вычисления сначала. Поэтому в случае, если неизвестно, сколько членов следует взять, их число можно увеличивать до тех пор, пока их вклад не станет пренебрежимо малым.
Используя другие разности, получаются другие интерполяционные схемы, например метод Ньютона для интерполяции назад, метод Гаусса для интерполяции вперёд и назад.
Итерационные методы интерполяции методы основаны на повторном применении простой интерполяционной схемы. Наиболее известным из них является метод Эйткена, сущность которого состоит в повторном применении линейной интерполяции. Следует, однако, отметить, что метод Эйткена не требует, чтобы используемые для интерполяции значения функции были расположены через равные интервалы.

23
3. ПРИБЛИЖЕНИЕ КРИВЫХ
Выше были описаны методы нахождения функции, проходящей через все заданные исходные точки. Однако на практике в исходных данных часто присутствуют шумы, искажающие реальную информацию.
3.1. МЕТОДЫ АППРОКСИМАЦИИ
Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяции) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости [3].
Близость исходной и аппроксимирующей функций определяется числовой мерой – критерием аппроксимации (близости). Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от «экспериментальных» (т. е. заданных), – критерий близости в заданных точках:
n |
β |
( y − yрасчет. )2 . |
|
|
R = ∑ |
|
|
||
|
i |
i i |
|
|
i =1 |
|
|
|
|
Здесь уi – заданные табличные значения функции; y |
расчет. |
– расчет- |
||
|
|
i |
|
|
ные значения по аппроксимирующей функции; βi, – весовые коэффициенты, учитывающие относительную важность i-й точки (увеличение βi, приводит при стремлении уменьшить R, к уменьшению, прежде всего отклонения в i-й точке, т. к. это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).
Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.
Другим распространенным критерием близости является следую-
щий:
R = max yi − yiрасчет. .
i
24
Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.
В обоих рассмотренных случаях в качестве значения функции yi можно брать не только абсолютные, но и относительные значения, например, yi/yn и др.
3.1.1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ФУНКЦИЙ
Как уже отмечалось, при решении задач аппроксимации следует уделять внимание выбору критерия, характеризующего качество приближения. Максимальное расстояние точек от кривой представляется вполне разумным критерием, однако, часто его использование порождает сложные вычислительные проблемы. В принципе, необходимо достижение некоторого компромисса между тем, что интуитивно кажется желательным, и тем, что оказывается реальным с вычислительной точки зрения. Обычно стремятся свести к минимуму сумму квадратов разностей между значениями функции, определяемыми выбранной кривой и заданной кривой.
Такой метод подгонки называют методом наименьших квадратов для функций.
На практике часто приходится иметь дело со случаем, когда значения функции заданы с некоторой погрешностью. Например, они могут быть результатами каких-либо измерений. Если погрешность исходных данных относительно велика, то это крайне неблагоприятно влияет на поведение интерполяционного сплайна и особенно его производных. В частности график сплайна имеет резко выраженные осцилляции. Поэтому возникает вопрос, нельзя ли построить сплайн, проходящий вблизи заданных значений, но более «гладкий», чем интерполяционный. Такие сплайны называются сглаживающими, а процедура их построения сглаживанием
Пусть функция задана n + 1 точками (x0, y0), (x1, y1), ... , (xn, yn) и требуется найти аппроксимирующую кривую G(x) в диапазоне x0 ≤ x ≤ xn. В этом случае погрешность в каждой точке составит:
Ei = G(xi ) − yi .
Тогда сумма квадратов погрешностей определится выражением:
n |
n |
|
E = ∑ E = ∑ |
[G(x ) − y ]2 . |
|
i |
|
i i |
i = 0 |
i = 0 |
|
Обычно функцию G(x) выбирают в виде линейной комбинации:
25
G(x) = c1G1(xi) + c2G2(xi) + ... + ckGk(xi).
Условие минимума Е определяются из уравнений частных производных, приравненных к нулю:
|
|
|
|
|
∂E |
= |
∂E |
= ... = |
∂E |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∂c1 |
∂c2 |
∂ck |
|
|
|
|
|
|
|
||
|
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
|
|
E = ∑[ c G (x ) + c G (x ) + ... +c G (x ) − y ]2 |
, |
|
|
|||||||||||
|
|
|
|
1 1 i |
2 2 i |
|
k k i |
|
i |
|
|
|
|
|||
|
|
|
|
i = 0 |
|
|
|
|
|
|
|
|
|
|
||
то это условие эквивалентно системе уравнений |
|
|
|
|
|
|
||||||||||
|
∂E |
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= 2 ∑[c1G1 (xi ) + ... + ck Gk (xi ) − yi ]G1 (x1 ) = 0 |
|
|
||||||||||
∂c1 |
|
|
||||||||||||||
|
|
i = 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
. |
|
|
|
|
|
∂E |
= 2∑[c1G1 (xi ) + ... + ck Gk (xi ) − yi ]Gk (xk ) = 0 |
|
|
|||||||||||
∂c |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти k уравнений, очевидно после открытия скобок, можно предста- |
|||||||||||||||
вить в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑G12 (xi ) |
|
|
∑G1 (xi )G2 (xi ) . . . ∑G1 (xi )Gk (xi ) |
|
c1 |
|
∑G1 (xi )yi |
|
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
|
∑G1 (xi )G2 (xi ) |
∑G22 (xi ) |
|
. . . ∑G2 (xi )Gk (xi ) |
|
c2 |
= |
∑G2 |
(xi )yi |
. |
||||||
|
|
|
|
. . . |
|
|
|
|
. . . |
. . . |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
ck |
|
∑G (x ) y |
|
|
|
∑G1 (xi )Gk (xi ) |
. . . |
|
|
. . . ∑Gk (xi ) |
|
|
|
k |
i k |
|
|||||
|
|
|
|
|
|
|
||||||||||
Так как элементы матрицы в левой части и вектор-столбца в правой определяются табличными данными, то выписанная система k линейных уравнений с k неизвестными может быть решена. Можно выбрать любую функцию Gi(x), лишь бы она была линейной относительно своих коэффициентов (например, ax + b). Фактический выбор функции Gi(x) должен осуществляться с учётом специфики табличных данных, под которой понимается их периодичность, экспоненциальный или логарифмический характер, свойства симметрии и наличие асимптотики.
Иногда таблицу разбивают на несколько частей и подбирают отдельную аппроксимирующую кривую для каждой части, в тех случаях, когда есть основания полагать, что аппроксимируемые данные соответствуют разным физическим состояниям системы. Пользуясь приближённой фор-

26
мулой, не следует выходить за пределы интервала, в котором она справедлива.
Если при построении аппроксимирующей функции в качестве Gi(x) используют ортогональные полиномы, для которых
∑Gj(xi)Gk(xi) = 0 при j ≠ i,
то матрица выписанной выше системы уравнений окажется диагональной, а выражения для коэффициентов cj упростятся:
n
∑ G j (xi )yi
c j = |
i = 0 |
. |
n |
∑G2j (xi )
i = 0
Это существенно облегчает задачу, и именно во многих стандартных программах подгонки кривых используют ортогональные полиномы.
Реальный выбор порядка того полинома, который будет использован для приближения по методу наименьших квадратов, зависит от природы экспериментальных данных. Естественно, он должен быть меньше, чем полное число точек, заданных таблицей. Вообще говоря, полином более высокого порядка приведет к результатам лучшим, чем полином меньшего порядка. Цена, которую придется заплатить за это лучшее представление, состоит в том, что теперь потребуется решать систему с большим числом неизвестных, коэффициентов и, следовательно, уравнений. Это приведет к программе, которая потребует больше памяти и больше времени на выполнение. Повышать порядок полинома следует с осторожностью, поскольку в тех случаях, когда этот порядок достигает предельно допустимых значений, решение может начать осциллировать между данными и тем самым сильно исказить общее поведение данных. Если это произойдет, имеет смысл попробовать различные порядки полиномов и выбрать тот, который приводит к наиболее разумному результату.
Пример [3].
Необходимо найти аппроксимирующую функцию в виде линейного полинома у = ао + а1x по имеющимся экспериментальным данным.
x |
–26 |
–22 |
–16 |
–11 |
–5 |
3 |
10 |
25 |
42 |
|
|
|
|
|
|
|
|
|
|
у |
66,7 |
71,0 |
76,3 |
80,6 |
85,7 |
92,9 |
99,4 |
113,6 |
125,1 |
|
|
|
|
|
|
|
|
|
|
Система нормальных уравнений будет выглядеть следующим обра-
зом:
27
|
|
n |
n |
|
a0 n + a1 ∑ xi = |
∑ yi , |
|
|
i = 1 |
i = 1 |
|
|
n |
n |
n |
|
a0 ∑ xi + a1 |
∑ xi2 = ∑ yi xi . |
|
|
i = 1 |
i = 1 |
i = 1 |
Используя имеющиеся данные, получим |
|||
n = 9; ∑ xi |
= 0; ∑ xi2 = 4060; ∑ yi |
= 811, 3; ∑ yi xi = 3534,8 . |
|
i |
i |
i |
i |
Решим полученную систему линейных уравнений относительно a0 и
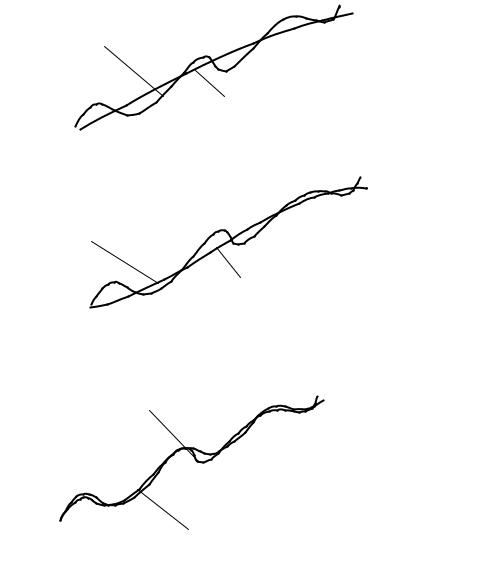
а1, получим a0 = 90,1, а1 = 0,87 (рис. 3.1).
Исходная функция f(x)
Аппроксимирующая функция fa(x)
M = 2
а)
Исходная функция f(x)
Аппроксимирующая функция fa(x)
M = 3
б)
Исходная функция f(x)
Аппроксимирующая функция fa(x)
M = 5
в)
Рис 3.1. Влияние степени аппроксимирующего полинома М на точность аппроксимации:
а) М = 2; б) М = 3; в) М = 5

28
3.1.2. МЕТОД ЧЕБЫШЕВА
Этот метод в основном являемся иллюстрацией решения третьей проблемы интерполяции: выбор узлов аппроксимации (если, конечно, это возможно при решении конкретной задачи) для получения при заданном числе узлов минимально возможной погрешности. Применение метода Чебышева позволяет обосновать размещение узлов интерполяции в заданных пределах на числовой оси. Предварительно переменная х преобразуется в переменную z, изменяющуюся от –1 до 1 при изменении от х0 до
хn [3]. |
|
|
||
z = − |
x0 + xn |
+ |
2x |
. |
|
|
|||
|
xn + x0 |
xn − x0 |
||
В свою очередь переменная z на интервале [–1, 1] формирует узлы следующим образом:
iπ zi = − cos .
n
Из этого соотношения видно, что узлы интерполяции располагаются неравномерно, сгущаясь к концам отрезка [x0, xn]. В вычислительном плане для интерполяции можно пользоваться интерполяционной формулой Лагранжа.
Пример применения метода не приводится, т. к. этот метод не дает ничего нового с точки зрения вычислений
3.1.3. МЕТОД РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
Равномерным приближением называется аппроксимация, в которой в качестве критерия близости используется модуль максимального отклонения расчетных и заданных значений. При этом решается задача минимизации этого критерия [3], т. е.
R = max yi − yiрасчет. → min .
Принято считать, что наилучшее равномерное приближение обеспечивает несколько лучшую аппроксимацию, чем среднеквадратичное. Однако теоретические оценки показывают незначительность такого преимущества; оно более значительно для функций с непрерывными старшими производными, не слишком большими по абсолютной величине, при небольших объемах исходных данных. Однако существенный недостаток –
29
отсутствие эффективных вычислительных алгоритмов (кроме прямого поиска min R методами нелинейного программирования, причем необходимо применять методы, пригодные для недифференцируемых функций) – делает малоприменимым данный способ аппроксимации.
3.2. СГЛАЖИВАНИЕ
Существуют различные возможности задания кривой [1]. При решении одних прикладных задач допустимо представление кривой в виде последовательности пикселов, а при решении других предпочтительно задавать с помощью математического выражения. Последнее может оказаться значительно компактнее дискретных представлений. Как уже говорилось выше, существует два основных подхода к представлению табличных данных (последовательности пикселов) кривыми. Отыскание кривой (возможно, кусочно-гладкой), проходящей через заданное множество точек, составляет задачу интерполирования, а отыскание кривой, проходящей вблизи заданного множества точек (т. е. необязательно проходящей через все точки) – задачу аппроксимации. Второй подход называют подгонкой кривой, которую стремятся провести так, чтобы её отклонения от табличных данных были минимальными (метод наименьших квадратов).
С математической точки зрения задачи интерполирования, вероятно, решать легче, однако при решении многих прикладных задач аппроксимация оказывается более практичной, т. к. точные значения обрабатываемых данных искажаются из-за наличия шума. Компромиссным решением при выборе одного из этих методов служит выделение множества точекориентиров, которые могут быть определены пользователем в интерактивном режиме, и проведения кривой вблизи этих точек (метод Чебышева).
Часто решающее значение при построении кривых по точкам приобретает выбор математического описания (функции). Распространение получили методы, предусматривающие использование многочленов и кусоч- но-полиномиальных функций различных типов.
Следует отметить также широкие возможности сглаживания кривых простым усреднением. Для этого применяются формулы для нахождения среднего значения [5]:
yi = (yi + yi + 1)/2,
или более сложного вида:
yi = (yi – 1 + yi + yi + 1)/3;
yi= (yi – 2 + yi – 1 + yi + yi + 1 + yi + 2)/5;

30
i +2
yi = (ai −2 yi −2 + ai −1 yi −1 + ai yi + ai +1 yi +1 + ai +2 yi +2 ) / ∑ ai и т. д. ,
i −2
где аi – целые числа.
Основным недостатком интерполирования с помощью многочленов являются существенные колебания, которые может претерпевать кривая, построенная между двумя точками. Причина подобного поведения интерполяционных многочленов заключается в том, что многочлен, в принципе, представляет собой сумму степенных функций. Эти функции обладают тем свойством, что их значения на всём сегменте определяются значением на произвольно малом подсегменте. Подбирая коэффициенты многочлена таким образом, чтобы сумма составляющих его функций принимала в нескольких точках искомые значения, контролировать значения отдельных членов в остальных точках невозможно. Примеры [1] показывают, что интерполирование многочленами имеет смысл только при сравнительно небольших сегментах. Оно заслуживает внимания лишь в том отношении, что образует в некотором смысле основу для более приемлемых способов построения кривых по точкам. Однако не следует считать, что кусочномногочленное интерполирование всегда даёт лучший результат, чем интерполирование с помощью многочленов. Если область определения делится не удачно, то все преимущества кусочной аппроксимации полностью исчезают.
3.3. МЕТОД СПЛАЙНОВ
Наибольшее распространение получала интерполяция с помощью кубических сплайнов. Сплайн – это функция, которая на каждом межузловом интервале совпадает с некоторым полиномом, разным для каждого интервала. Полиномы соседних интервалов стыкуются таким образом, чтобы функция была непрерывной. Дополнительно требуют непрерывности нескольких производных (в кубических сплайнах – двух производных)
Сплайн представлен графически на рис. 3.2 [1 – 5].
f(x)
Sn,ν(x)
0 |
x1 x2 |
xi |
xN |
x |
Рис. 3.2. Сплайн одной переменной
