Малышев Вычислительная математика EQ3

61

по x, получаем, что производная функции f ′(x) на отрезке [xk, xk + 1] приближается разделённой разностью L′1 (x) = f [xk, xk + 1], которая называется конечно-разностной аппроксимацией производной по двум точкам.

Остаточный член аппроксимации R′1(x) = L′1(x) – f ′(x). Повторяя рассуждения, по аналогии с выше сказанным находим:

Максимальное значение правой части достигается на концах отрезка [xk, xk + 1]. Получаем:

Все приведённые оценки погрешности интерполяции многочленами улучшить нельзя. Это значит, что существуют такие функции f(x) в рассматриваемом классе, что в оценках либо имеет место знак равенства, либо равенство достигается, если константу уменьшить на произвольно малую величину. В частности, оценка максимальной погрешности точна для многочленов второй степени, когда f ″(x) = const.

5.3. КОНЕЧНО-РАЗНОСТНАЯ АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ (ТРЁХТОЧЕЧНАЯ СХЕМА)

Дифференцируя L2(x), получаем формулу аппроксимации производной [2]

В частности, в узлах интерполяции имеем

f0′ = (1 + µ1 ) f [ x0 , x1 ] − µ1 f [ x1 , x2 ] ; f1 = λ1 f [x0 , x1 ] + µ1 f [ x1 , x2 ];

f2 = −λ1 f [ x0 , x1 ] + (1 + λ1 ) f [ x1 , x2 ] ,

где λ1 = h1(h0 + h1)–1, µ1 = 1 – λ1.

Это – формулы конечно-разностной аппроксимации производной по трем точкам. Они приближают производную функции f(t) C(2) [x0, x2], в узлах интерполяции с точностью

где K10 = K12 = 2/3, K11 = 1/2.

где K10 = K12 = 1/3, K11 = 1/6.

В обоих случаях коэффициент K11, отвечающий x = x1, меньше, чем K10 = K12. Это значит, что в средних узлах конечно-разностная аппроксимация дает более точное приближение, чем в крайних.

Рассмотрим, наконец, аппроксимацию второй производной функции f ″(x). Отметим, что речь может идти только о непрерывной функции. Дифференцируя L2(x), находим

где K20 = K22 = 1, K21 = 1/3.

5.4. КОНЕЧНО-РАЗНОСТНАЯ АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ (ЧЕТЫРЁХТОЧЕЧНАЯ СХЕМА)

Кубической интерполяции соответствует аппроксимация производных в узлах [2]

f1′ = (λ1 − λ1σ1 ) f [x0 , x1 ] + (µ1 + λ1σ1 + µ2σ1 ) f [x1 , x2 ] − µ2σ1 f [x2 , x3 ].

Вторые производные аппроксимируются так:

63

где K10 = K13 = ¼, K11 = K12 = 1/12.

Оценки погрешности формул

где K20 = K23 = 11/12, K21 = K22 = 1/6.

6. МЕТОДЫ ИНТЕГРИРОВАНИЯ

При анализе инженерных и научных данных часто возникает необходимость найти наклон кривой или площадь под кривой. Для решения этих задач можно воспользоваться графическим методом, однако, нередко точность таких операций ограничивает пригодность получаемых результатов. По этой причине необходимы численные процедуры дифференцирования и интегрирования.

Численные методы вычисления применяют в тех случаях, когда интеграл не удаётся сосчитать в аналитическом виде или когда этот вид достаточно сложен. Численное интегрирование применяют и тогда (как в нашем случае), когда нужно найти интеграл от табулированной функции, измеряемой в эксперименте. Как показано на рис. 5.1, г, численное интегрирование, называемое также численной квадратурой, является устойчивой процедурой и, в отличие от численного дифференцирования, имеет тенденцию снижать влияние погрешности данных на окончательный результат. Методы численного интегрирования основаны на аппроксимации определённого интеграла суммой составных площадей. В общем виде задача состоит в нахождении величины [1]

b

I = ∫ f ( x) dx .

a

Методы численного интегрирования (табл. 6. 1) подразделяются в соответствии с тем, равномерно ли распределены взятые значения абсцисс на оси. Формулы Ньютона-Котеса требуют равноотстоящих друг от друга значений на оси абсцисс, а формулы Гаусса – нет.

64

Таблица 6.1

Методы численного интегрирования

6.1.Интегрирование по методу прямоугольников

Кпростейшим методам можно отнести методы прямоугольников (левых и правых) и трапеций. В первом случае подынтегральная функция

заменяется горизонтальной прямой (y + c0) со значением ординаты, т. е. значения функции соответственно слева или справа участка, во втором

случае – наклонной прямой (y + c1x + c0). Формулы интегрирования при разбиении отрезка [a, b] на n частей с равномерным шагом h соответственно приобретают вид [3]:

– для одного участка интегрирования:

b

I = ∫ f ( x)dx ≈ f (a)(b − a) = f ( x0 )h ;

a

b

I = ∫ f ( x)dx ≈ f (b)(b − a) = f ( x1 )h ;

a

ω0 = h = const ;

где x0 = a, x1 = b, h = b – a;

– для n участков интегрирования:

65

Нетрудно заметить, что в методе прямоугольников интеграл вычислится абсолютно точно только при f(x) = c(const), а в методе трапеций – при f(x) линейной или кусочно-линейной.

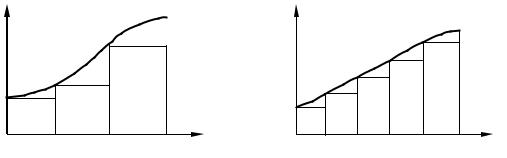
На рис. 6.1 для сравнения приведены примеры прямоугольников при различном числе участков. Наглядно видно, что площадь всех прямоугольников на правом рисунке меньше отличается от площади под кривой f(x), чем на левом.

Метод прямоугольников не находит практического применения в силу значительных погрешностей, что тоже видно из рис. 6.1.

Рис. 6.1. Иллюстрация метода левых прямоугольников: a) с 3 участками разбиения отрезка интегрирования [a, b]; б) с 5 участками разбиения отрезка интегрирования [a, b]

6.2. ИНТЕГРИРОВАНИЕ ПО МЕТОДУ ТРАПЕЦИЙ

Простейшей из всех формул Ньютона-Котеса является формула для метода трапеций [1, 3]. Этот метод основан на линейной аппроксимации интегрируемой функции между соседними заданными точками (xi, yi) и (xi + 1, yi + 1) на промежутке a ≤ x ≤ b. Таким образом, если x0 = a и xn = b, ин-

66

тегралу соответствует сумма площадей n трапеций, каждая из которых имеет высоту h. Значение интеграла записывается через заданные ординаты (см. табл. 6.1).

Метод трапеций представлен графически на рис. 6.2. Он даёт удовлетворительное приближение интеграла в том случае, когда кусочки площадей между верхними сторонами трапеций и кривой малы. В общем случае сумма этих площадей зависит от вида подынтегральной функции и ширины полоски lim∑Si = I при h → 0. Значения этой ошибки называют ошибкой усечения.

y

y = f(x)

y1

y0

x x0 x1

Рис. 6.2. Метод трапеций

S0 = (y0 + y1)/2(x1 – x0) = (y0 + y1)/2h;

S1 = (y2 + y1)/2(x2 – x1) = (y2 + y1)/2h;

S = S1 + S2 = (y0 + 2y1 + y2)/2h и т. д.

Предположим, что для одной трапеции на промежутке от xi до xi + 1

xi +1

I = ∫ f (x) dx = F (xi +1 ) − F (xi ) ,

xi

где F(xi) – первообразная в точке xi.

Этот интеграл равен сумме площади трапеции и погрешности аппроксимации:

I = ∑Si + δ;

I = h[f(xi + h) + f(xi)]/2 +δ.

Из этих двух неравенств погрешность находят в виде:

δ = I – ∑Si;

67

δ = F(xi + 1) – F(xi) – (h[f(xi + h) + f(xi)])/2.

Разложение в ряд Тейлора F(xi + 1) даёт:

F(xi + 1) = F(xi + h) = F(xi) + hF′(xi) + h2F ″(xi)/2! + h3F′″(xi)/3! + Θ(h4).

Вэтом представлении старшие члены имеют порядок h4. Разложение

вряд Тейлора f(xi + h) даёт:

f(xi + h) = f(xi) + hf ′(xi) + h2f ″(xi)/2! + h3f ′″(xi)/3! + Θ(h4).

Пусть старшие члены имеют порядок h4 и являются малыми по сравнению с первыми. Если принять во внимание, что f(xi) = F ′(xi), f ′(xi) = = F ″(xi) и f ″(xi) = F ″′(xi) и вычислить погрешность, подставив эти равенства в ряд Тейлора, получим:

ζ = – h3 f ″(xi)/12 + Θ(h4);

δ= – h3 f ″(xi)/12.

Если ширина шага мала, слагаемое с h3 окажется определяющим и более высокими степенями можно пренебречь. Таким образом, погрешность усечения в методе трапеций зависит от второй производной интегрируемой функции. Для определения погрешности при n интервалах разбиения нужно просуммировать погрешности для каждого интервала.

Если вторая производная на промежутке интегрирования меняется слабо, можно воспользоваться её средним значением:

ni =1

ис учётом xi + 1 = xi + nh записать суммарную погрешность в виде:

пропорциональна квадрату ширины шага. Это означает, что с уменьшением размера промежутка вдвое погрешность усечения уменьшается в 4 раза.

Однако с увеличением числа отрезков разбиения начинает преобладать погрешность округления, возникающая при сложении большого количества чисел. Cуществует оптимальное значение ширины шага h. Ра-

68

зумное значение этой величины определяется в ходе вычислений экспериментальным путём, т. к. получить его в аналитическом виде обычно не представляется возможным.

Пример [3].

на четыре участка. Аналитическое вычисление данного интеграла дает I = = arctg(1) – arctg(0) = 0,7853981634. В нашем случае:

h = 1; x0 = 0; x1 = 1;

h = 0,25(1/4); x0 = 0; x1 = 0,25; x2 = 0,5; x3 = 0,75; x4 = 1;

1

f ( x) = 1 + x2 .

Получим методом левых прямоугольников:

69

6.3. ИНТЕГРИРОВАНИЕ ПО МЕТОДУ СИМПСОНА

Одним из путей уменьшения ошибки в процессе численного интегрирования является использование иного, чем прямая линия (метод трапеций), вида аппроксимирующей кривой на малом отрезке интегрирования. Из этого предположения естественным образом следует, что нужно взять кривую более старшего порядка, а именно параболу. Разумеется, парабола требует уже не двух, а трёх соседних точек табулированных значений, так что в результате формула для интеграла будет другой, чем в методе трапеций. Новая формула, известная как формула Симпсона, имеет вид [1]:

Это равенство применяют для чётного числа промежутков. Погрешность усечения в методе Симпсона может быть представлена в виде:

E = –(xi + n – xi)* h4 * f IVср. /180,

где f IVср. означает среднее значение четвёртой производной функции f(x) на промежутке (xi, xi + n). Суммарная погрешность пропорциональна четвёртой степени интервала разбиения. Это означает, что при делении интервала пополам – погрешность уменьшается в 16 раз. Такой метод, безусловно, имеет преимущества по сравнению с методом трапеций.

При использовании метода Симпсона может случиться так, что количество промежутков нечётно. Этой трудности можно избежать, если для первых трёх промежутков применять следующую формулу, использующую параболу третьей степени, проходящую через четыре первые точки:

A3 = (3h/8)(y0 + 3y1 + 3y2 + y3).

Эта формула известна как формула Симпсона трёх восьмых.

Пример [3].

Рассмотрим вычисление интеграла из предыдущего примера. В случае одного участка будем иметь x0 = 0, x1 = 0,5, x2 = 1, h = 0,5.

70

6.4. ФОРМУЛЫ ИНТЕГРИРОВАНИЯ НЬЮТОНА-КОТЕСА СТАРШИХ ПОРЯДКОВ

Тот факт, что формулы интегрирования легко находятся для многочленов первой и второй степени, приводит к желанию обобщить эту процедуру для многочленов старших порядков. Общий вид результатов приведён в табл. 6.1 с учётом, что n – количество отрезков разбиения, k – степень используемого полинома, x* – принадлежит промежутку [a, b], f(k)(x*) – производная k-го порядка функции f(x), вычисленная в точке x*, h – шаг разбиения. Коэффициенты C0, C1 и wi берутся из специальных таблиц (табл. 6.2) [1]. Для большого числа наборов (например, при k = 2 и n = 6) нужно сложить коэффициенты таким образом, чтобы последние

Это даёт:

что совпадает с ранее полученным результатом. Последнее слагаемое в формуле Ньютона-Котеса показывает порядок погрешности, связанной с аппроксимацией. Очевидно, что при малых h(<1) значения hk + 1 тем более мало. Однако этим соображением необходимо пользоваться с осторожностью, т. к. погрешность зависит и от f (k)(x*). Существуют такие функции, для которых производные высоких порядков становятся очень большими и для них не удаётся снизить погрешность за счёт увеличения k.

Формулы Ньютона-Котеса, несмотря на их внешнюю привлекательность, используют редко, поскольку они достаточно громоздки и имеют большую ошибку округления. Если при интегрировании потребуется более высокая точность, обычно применяют метод Ромберга или квадратур-