
- •3. Циклы поршневых двигателй внутреннего сгорания (двс)
- •3.1. Принцип действия двс
- •3.2. Цикл со смешанным подводом тепла
- •3.4. Термодинамика идеального цикла Дизеля
- •3.5. Индивидуальное задание по термодинамическому расчету необратимых циклов поршневых двигателей
- •3.6. Указания к выполнению задания
- •3.7. Описание программы
- •3.8. Пример выполнения задания
- •4. Газотурбинные установки
- •4.1. Гту со сгоранием при постоянном давлении
- •4.2. Цикл газотурбинной установки с подводом тепла
- •4.3. Цикл газотурбинной установки со сгоранием
- •4.4. Газотурбинная установка со сгоранием при
- •4.5. Индивидуальное задание по термодинамическому
- •4.6. Указания к выполнению задания
- •4.7. Описание программы
- •4.8. Пример выполнения задания
- •0 Дж/кгДж/кгДж/кгДж/кг.
- •5. Элементы химической термодинамики
- •5.1. Закон Гесса и его следствия
- •5.2. Зависимость теплового эффекта химической
- •5.3. Задание по расчету теплового эффекта
- •5.4. Пример расчёта
- •5.5. Закон действующих масс. Константы равновесия
- •5.6. Степень завершенности реакции и состав
- •5.7. Термодинамические уравнения процесса протекания
- •5.8. Методы расчета констант равновесия
- •Метод Темкина-Шварцмана
- •5.9. Индивидуальные задания по определению
- •5.10. Примеры выполнения заданий
4.2. Цикл газотурбинной установки с подводом тепла
при
![]() и изотермическим сжатием
и изотермическим сжатием
В
принципе практическая реализация такого
цикла невозможна. Однако применение
многоступенчатого сжатия с промежуточным
охлаждением, а также интенсивное
охлаждение цилиндров либо других
конструкционных элементов, соприкасающихся
со сжимаемым газом при его сжатии,
позволяют заметно приблизить процесс
к изотермическому. На рис. 4.3, 4.4
показаны
![]() ,
,![]() и
и![]() ,
,![]() -диаграммы
процесса сжатия в компрессоре с
изотермическим сжатием.
-диаграммы
процесса сжатия в компрессоре с
изотермическим сжатием.
Очевидно, что в этом цикле отведенное тепло равно сумме теплот, отводимых в изотермическом процессе сжатия 1-2 и изобарном расширении 4-1.
![]() ;
(4.8)
;
(4.8)
![]() .
(4.9)
.
(4.9)
Рис.
4.3.
ГТУ
с изотермическим сжатием
ГТУ с изотермическим сжатием

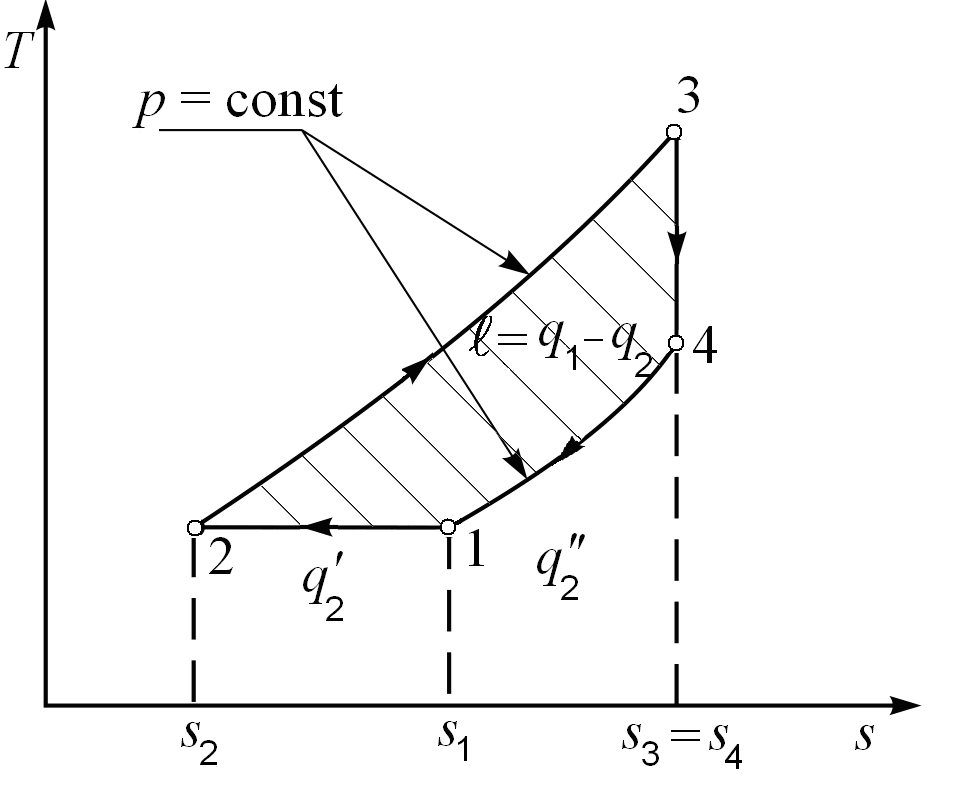
![]() ,
,
![]() -диаграмма
цикла Рис. 4.4.
-диаграмма
цикла Рис. 4.4.
![]() ,
,![]() -диаграмма
цикла
-диаграмма
цикла
Термодинамический
анализ цикла ГТУ со сжатием при
![]() ,
предполагает все допущения, которые
были приняты при анализе предшествующих
циклов, в том числе и при рассмотрении
цикла ГТУ со сжатием по адиабатному
процессу. Рабочее тело – идеальный газ
постоянного химического состава.
,
предполагает все допущения, которые
были приняты при анализе предшествующих
циклов, в том числе и при рассмотрении
цикла ГТУ со сжатием по адиабатному
процессу. Рабочее тело – идеальный газ
постоянного химического состава.
Процессы рабочего цикла квазистатичны и являются частными случаями политропных процессов. Отвод отработавших газов в окружающую среду заменен изобарным процессом расширения рабочего тела. Расширение на турбине осуществляется до давления среды, в которую происходит истечение.
Параметры рабочего тела в узловой точке 1 предполагаются известными. Однозначность расчетного анализа достигается заданием параметров, определяющих характер реализуемого цикла.
Степень сжатия воздуха в компрессоре:
![]() .
(4.10)
.
(4.10)
Степень предварительного расширения, в принципе характеризующая подвод тепла по изобаре 2-3:
![]() .
(4.11)
.
(4.11)
Параметры в начальной точке цикла будем считать известными.
Состояние
1:![]() ,
,![]() ,
,![]() .
.
Найдем выражение для расчета параметров в узловой точке цикла 2.
Температура
![]() – по определению цикла.
– по определению цикла.
Давление
![]() ,
исходя из заданной степени сжатия
воздуха в компрессоре.
,
исходя из заданной степени сжатия
воздуха в компрессоре.
Для
определения удельного объема
![]() воспользуемся соотношением параметров
в изотермическом процессе:
воспользуемся соотношением параметров
в изотермическом процессе:
![]() ;
;
![]()
или с учетом (4.10)
![]() .
(4.12)
.
(4.12)
Состояние
2:
![]() ;
;![]() ;
;![]() .
.
Определим
параметры рабочего тела в узловой точке
3 рабочего цикла, воспользовавшись
соотношением параметров изобарного
процесса 2-3 и заданной величиной степени
предварительного расширения
![]() (4.11).
(4.11).
Давление в точке 3:
![]() .
.
Исходя
из соотношения параметров в изобарном
процессе
![]() ,
найдем
,
найдем![]() :
:
![]() .
.
Удельный
объем в состоянии 3 также в
![]() раз больше чем в состоянии 2:
раз больше чем в состоянии 2:
![]() .
.
Состояние
3:
![]() ,
,![]() ,
,![]() .
.
Исходя
из цикла, давление в точке 4 равно давлению
в точке 1. Объем в точке 4 найдем, записав
соотношение параметров для адиабаты
3-4:
![]() ,
откуда
,
откуда
![]()
или
![]() .
.
Температуру
в точке 4 найдем воспользовавшись
уравнением состояния
![]() ,
тогда
,
тогда![]() .
.
Учтем,
что
![]() и получим
и получим![]() .
.
Состояние
4:
![]() ;
;![]() ;
;![]() .
.
Рассчитаем энергетические характеристики цикла.
От
высокотемпературного источника к
каждому килограмму рабочего тела по
изобаре 2-3 подведена теплота
![]()
![]() .
(4.13)
.
(4.13)
Сбрасываемое
в окружающую среду тепло
![]() состоит из суммы тепла
состоит из суммы тепла![]() ,
отведенного по изобаре 4-1, и
,
отведенного по изобаре 4-1, и![]() ,
отведенного по изотерме 1-2:
,
отведенного по изотерме 1-2:
![]() .
.
Найдем
составляющие теплоты
![]() .
.
Для изобары 4-1:
![]() .
.
Для изотермы 1-4:
![]() .
(4.14)
.
(4.14)
Тогда
![]() .
(4.15)
.
(4.15)
Полезная работа за цикл, полученная от каждого килограмма рабочего тела:
![]() .
(4.16)
.
(4.16)
Термический КПД цикла:
![]() ;
;
 .
(4.17)
.
(4.17)
Преобразуем термический КПД к более удобному для анализа виду:
 .
(4.18)
.
(4.18)
Рис.
4.5. Зависимость термического КПД от
степени предварительного расширения

![]() [6]
[6]![]() для различных значений степени сжатия
в компрессоре
для различных значений степени сжатия
в компрессоре![]() (для
(для![]() )
приведена на рис. 4.5.
)
приведена на рис. 4.5.
Исследуем
функцию
![]() на наличие максимума для фиксированной
степени предварительного расширения
на наличие максимума для фиксированной
степени предварительного расширения![]() .
Продифференцируем
.
Продифференцируем
![]() ,
предполагая
,
предполагая
![]() :
:
![]() .
.
Приравнивая
![]() к нулю, получим условие максимума
термического КПД:
к нулю, получим условие максимума
термического КПД:
![]() .
.
При этом термический КПД принимает максимальное значение:
![]() .
(4.19)
.
(4.19)
Линия максимальных значений термического КПД на рис. 4.5 нанесена пунктиром.
Нетрудно
заметить, что термический КПД цикла
растет с ростом степени повышения
давления
![]() ,
ростом показателя адиабаты. Для
фиксированных значений
,
ростом показателя адиабаты. Для
фиксированных значений![]() и
к КПД несколько возрастает с ростом
степени предварительного расширения
и
к КПД несколько возрастает с ростом
степени предварительного расширения![]() .
Однако с увеличением степени повышения
давления в цикле влияние
.
Однако с увеличением степени повышения
давления в цикле влияние![]() на
КПД существенно снижается.
на
КПД существенно снижается.
