
matstatistika_1_2_3_RGR
.pdfБайкальский государственный университет экономики и права Кафедра математики
Шерстянкина Н.П.
Выполнение расчетно-графических работ по дисциплине Математическая статистика
сиспользованием MS Excel
Методические указания
Иркутск 2009 |
|
СОДЕРЖАНИЕ |
|
1.Математическая статистика |
3 |
1.1. Задание расчетно-графической работы № 1. Математическая |
|
статистика |
3 |
1.2. Тема 1. Описательная статистика. Основные формулы и ряды |
4 |
1.3. Выполнение расчетов в MS Excel |
9 |
1.3.1. Подготовка данных для анализа |
9 |
1.3.2. Построение точечного вариационного ряда 1 |
12 |
1.3.3. Построение интервального вариационного ряда 2 |
14 |
1.3.4. Построение точечных сгруппированных рядов 3–5 |
15 |
1.3.5. Построение графиков |
16 |
1.3.6. Эмпирическая функция распределения |
20 |
1.3.7. Вычисление числовых характеристик |
21 |
1.3.8. Оформление полученных результатов |
23 |
1.4. Тема 2. Статистическое оценивание параметров. Основные фор- |
|
мулы и расчеты. |
29 |
1.5. Тема 3. Статистическая проверка гипотез. Основные формулы и |
|
расчеты. |
31 |
2. Прикладные разделы математической статистики |
38 |
2.1. Задание расчетно-графической работы № 2. Однофакторный |
38 |
дисперсионный анализ |
|
2.1.1. Тема 4. Однофакторный дисперсионный анализ. Основные |
38 |
формулы и таблицы. |
|
2.1.2. Вычисления в MS Excel |
40 |
2.1.3. Оформление полученных результатов |
43 |
2.2. Тема 5. Построение модели парной линейной регрессии |
46 |
2.2.1. Основные формулы |
47 |
2.2.2. Вычисления в MS Excel (поле корреляции) |
53 |
2.2.3. Оформление результатов расчетов |
62 |
2
1.МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1.1.Задание расчетно-графической работы № 1.
Математическая статистика
общая сумма : 20 баллов
Тема 1: описательная статистика. Задание по выборке (объем выборки ≥
50): 10 б.
1.Дать экономическую интерпретацию исходным данным.
2.Построить точечный вариационный ряд, распределив значения по частотам
(ряд 1).
3.От точечного ряда перейти к интервальному, взяв число интервалов k (ряд 2).
4.От интервального ряда перейти к точечному сгруппированному ряду (ряд 3), распределив значения: а) по частотам и относительным частотам в виде доли или процента (ряд 4), б) по накопленным частотам (ряд 5).
5.Построить полигон частот для ряда 3 или 4, гистограмму для ряда 2, кумуляту для ряда 5.
6.Построить эмпирическую функцию распределения по ряду 4.
7.Определить числовые характеристики: выборочное среднее, моду, медиану (по точечному, интервальному рядам и графику), выборочную дисперсию, среднеквадратическое отклонение, коэффициент вариации, асимметрию, эксцесс.
8.Сделать вывод о близости к нормальному закону.
Тема 2: статистическое оценивание параметров |
5 б. |
1.Указать несмещенные оценки неизвестного математического ожидания и дисперсии случайной величины, выборка которой была представлена в теме 1.
2.Построить доверительные интервалы для неизвестного математического ожидания и дисперсии, в предположении, что выборка из нормальной генеральной совокупности и γ1 = 0,95, γ2 = 0,9 .
3.Метод моментов и ММП.
Тема 3: статистическая проверка гипотез |
5 б. |
Используя критерий согласия χ2 проверить гипотезу Н0 |
о нормальном |
распределении изучаемой случайной величины, выборка наблюдений которой представлена в теме 1.
3

1.2. Тема 1. Описательная статистика. Основные формулы и ряды1
Ряд 1: Точечный вариационный ряд (табл.1.1).
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
||
|
|
|
xi |
|
x1 |
|
x2 |
… |
|
xr |
|
|
|
|
|
ni |
|
n1 |
|
n2 |
… |
|
nr |
|
|
где r – число различных значений в выборке. |
|
|
|
|
||||||||
Ряд 2: интервальный ряд (табл. 1.2). |
|
|
|
|
|
Таблица 1.2 |
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
Ci−1 −Ci |
|
C0 −C1 |
|
C1 −C2 |
|
… |
Ck −1 −Ck |
||||
|
ni |
|
n1 |
|
|
n2 |
|
… |
|
nk |
||
k
где ∑ni = n .
i=1
Для построения ряда 2:
1) отмечаются наименьшее xmin и наибольшее xmax значения в выборке, и рассчитывается размах вариации:
R = xmax − xmin ; |
(1.1) |
2) для выборки объемом п значений берется число интервалов группирования
k ≈ log2 n +1 = ln n / ln 2 +1 =1,443 ln n +1; |
(1.2) |
|||||
3) находим шаг (длину) интервала: |
|
|
|
|
|
|
h = |
x max |
− x min |
= |
R |
; |
(1.3) |
|
k |
k |
||||
4) вычисляем границы интервалов: |
|
|
|
|||
|
|
|
|
|
||
C0 = xmin , C1 = C0 + h, |
C2 = C1 + h , …,Ck = Ck−1 + h . |
(1.4) |
||||
После построения интервалов нужно посчитать, сколько значений вошло в |
||||||
каждый интервал.
Ряд 3: точечный сгруппированный ряд (табл. 1.3) – распределение значений по частотам.
|
|
|
|
|
|
|
Таблица 1.3 |
|
|
xi* |
|
x1* |
|
x 2* |
… |
|
x k* |
где |
ni |
|
n1 |
|
n2 |
… |
|
nr |
xi* = |
Ci +Ci+1 |
|
|
(1.5) |
||||
|
|
|
||||||
|
|
|
|
|||||
– середина каждого интервала. |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|||
Ряд 4: точечный сгруппированный ряд (табл. 1.4) – распределение значений по относительным частотам.
1 Здесь и далее в качестве обозначений, формул и определений использованы данные учебного пособия: Ежова Л.Н. Эконометрика. Начальный курс с основами теории вероятностей и математической статистики. – Иркутск:
Изд-во БГУЭП, 2002. – 310 с.
4
|
|
|
|
|
|
|
|
Таблица 1.4 |
|
|
xi* |
|
x1* |
|
x 2* |
… |
x k* |
|
|
|
wi |
|
w1 |
|
w2 |
… |
wr |
|
|
где |
wi 100% |
w1 100% |
w2 100% |
… |
wr 100% |
|
|||
|
|
ni |
|
k |
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
wi = |
, |
∑wi =1. |
|
(1.6) |
|||
|
|
|
|
||||||
|
|
|
n |
i=1 |
|
|
|
||
Ряд 5: точечный сгруппированный ряд (табл. 1.5) – распределение значений по накопленным частотам.
|
|
|
|
|
Таблица 1.5 |
|
|
xi* |
x1* |
x 2* |
… |
|
x k* |
|
mi |
m1 |
m 2 |
… |
|
mr |
где |
|
|
|
|
|
|
m1 = n1, m2 = m1 + n2 , m3 = m2 + n3 …, mr = n . |
(1.7) |
|||||
Графики:
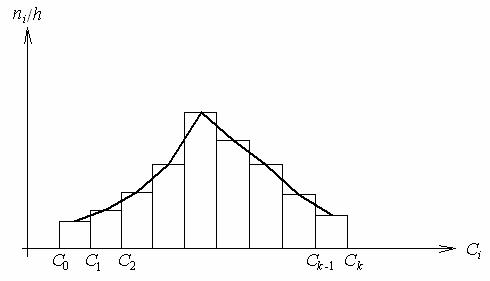
3. Гистограмма строится по ряду 2 (данные табл. 1.2, рис. 1.1), где по оси ординат вместо ni рассчитывается значение ni / h или ni /(h n).
Рис. 1.1. Гистограмма
2. Полигон частот или относительных частот строится по ряду 3 (данные табл. 1.3, рис. 1.2) или ряду 4 (данные табл. 1.4, рис. 1.2).
5

Рис. 1.2. Полигон частот (относительных частот) 3. Кумулята строится по ряду 5 (данные табл. 1.5, рис. 1.3):
Рис. 1.3. Кумулята
Эмпирическая функция распределения:
0, x ≤ x*, |
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
, x* |
< x ≤ x* , |
|
|
|||||
w |
|
|
||||||
1 |
1 |
|
|
|
|
2 |
|
|
w |
+ w |
2 |
, |
x* < x ≤ x*, |
(1.8) |
|||
F *(x) = 1 |
|
|
|
2 |
, x* |
3 |
||
w |
+ w |
2 |
|
+ w |
< x |
≤ x* , |
||
1 |
|
|
|
3 |
3 |
|
4 |
|
.... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
1, x > xk . |
|
|
|
|
||||
График эмпирической функции распределения представляет собой ступен- |
||||||||
чатую линию со скачками в точках x* |
, x* ,K, x* . |
|
||||||
|
1 |
|
|
|
2 |
k |
|
|
|
|
|
|
6 |
|
|
|
|

Рис. 1.4. График эмпирической функции распределения
Числовые характеристики
А. Меры положения
Среднее выборочное значение
|
|
1 |
k |
|
xв |
= |
|
∑ni xi* . |
(1.9) |
|
||||
|
|
n i=1 |
|
|
Медиана определяется как: 1) среднее по местоположению значение расположенного в порядке возрастания ряда наблюдений; 2) по интервальному ряду xmed по формуле:
xmed = xmed (min) + h |
n |
2 |
− m |
med −1 |
, |
(1.10) |
|
|
|||||
|
|
|
|
|||
|
|
|
nmed |
|
||
где xmed (min) – нижняя граница медианного интервала (сумма накопленных час-
тот в котором превышает половину объема выборки), h – шаг интервала, mmed −1 – накопленная частота интервала, предшествующего медианному, nmed –
частота медианного интервала; 3) по кумуляте (рис. 1.3), как значение выборки, соответствующее ее середине n /~2.
Модальное значение (мода) xmod – это такое наиболее часто встречающееся
значение исследуемого признака в данном вариационном ряду. Мода определеяется, как 1) для точечного ряда 3 соответствует выборочному значению с наибольшей частотой; 2) по интервальному по следующей формуле:
xmod = xmod(min) + h |
nmod − nmod−1 |
, |
(1.11) |
||
2nmod − nmod−1 |
− nmod+1 |
||||
|
|
|
|||
где xmod(min) – нижняя граница модального интервала (интервал с наибольшей частотой); h – интервальная разность; nmod – частота модального интервала; nmod−1 – частота интервала, предшествующего модальному; nmod+1 – частота
интервала, последующего за модальным; 3) по полигону частот (рис. 2) значение признака, соответствующее самой высокой точке.
7

Б. Меры разброса
Для удобства вычислений мер разброса и формы можно составить вспомогательную таблицу (табл. 1.6).
|
|
|
|
|
|
|
|
|
|
|
n (x* |
|
|
)3 |
|
|
Таблица 1.6 |
||||
k |
|
xi* |
ni |
xi* − xв |
n |
i |
(x* |
− x |
в |
)2 |
− x |
в |
n |
i |
(x* |
− x |
в |
)4 |
|
||
|
|
|
|
|
|
i |
|
|
i i |
|
|
|
i |
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
Итого |
∑ |
– |
|
|
∑ |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
||
Выборочная дисперсия используется для оценки разброса значений исследуемого признака.
|
|
1 |
n |
|
(x* − x |
|
)2 . |
|
|
D |
= |
∑n |
|
|
(1.12) |
||||
|
n |
|
|
||||||
в |
|
|
i=1 |
i |
i |
в |
|
|
|
Среднеквадратическое отклонение (СКО): |
|
||||||||
|
|
σв = |
Dв |
|
|
(1.13) |
|||
– дает абсолютный разброс значений признака относительного среднего.
Коэффициент вариации
V = |
σв |
100% |
(1.14) |
|
|||
|
xв |
|
|
– характеризует относительный разброс значений признака вокруг его среднего значения, выраженный в процентах.
Вывод: Среднее значение исследуемой случайной величины составляет:
xв ±σв
В. Меры формы
Коэффициенты асимметрии и эксцесса относятся к мерам, которые харак-
теризуют отклонение эмпирического распределения от нормального закона. Выборочный коэффициент асимметрии характеризует степень исперссти
и рассчитывается по формуле: |
|
= |
1 ∑n |
(x* − x |
|
)3 . |
(1.15) |
||||
A |
= μ3 , где μ |
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
s |
|
|
|
3 |
|
|
i=1 i |
i |
в |
|
|
|
σв3 |
|
|
n |
|
|
|||||
Для симметричных (относительно среднего значения) функций плотности Αs должен быть близок к нулю, в то время как для распределения, гистограмма
которого имеет «длинную часть», расположенную справа от ее вершины, Αs > 0, а если слева – Αs < 0. Для нормального закона As = 0.
Выборочный эксцесс Εk характеризует степень островершинности или плосковершинности распределения. Он рассчитывается по формуле:
8
|
|
|
μ4 |
|
|
~ |
|
1 n |
|
0 |
|
|
4 |
|
|
Ε |
k |
= |
|
−3, где μ |
|
= |
∑n |
(x |
|
− x |
|
) . |
(1.16) |
||
σв4 |
|
|
|
||||||||||||
|
|
|
Εk |
|
4 |
|
n i=1 i |
|
i |
|
в |
|
|
||
Для нормального закона |
= 0 , |
для островершинного (по сравнению с |
|||||||||||||
нормальным) распределения – |
Εk |
> 0 , а для плосковершинного – |
Εk < 0. Здесь |
||||||||||||
Εk < 0, значит, график имеет плоскую вершину. |
|
|
|
|
|
||||||||||
Вывод о близости эмпирического распределения к нормальному закону:
1.Полигон частот имеет колоколообразный (куполообразный) вид;
2.Выполняется условие: xв ≈ xmod ≈ xmed .
3.Коэффициенты асимметрии и эксцесса близки нулю.
4.Коэффициент вариации < 33%.
1.3.ВЫПОЛНЕНИЕ РАСЧЕТОВ В MS Excel
1.3.1.Подготовка данных для анализа. Самостоятельная генерация выбор-
ки
Если выборка уже выдана преподавателем, то достаточно выполнить только шаг 1 для настроек пакета анализа и поиска решения, остальные шаги можно пропустить. Если выборку нужно сгенерировать самостоятельно, то это можно сделать с помощью встроенных функций MS Excel следующим образом по указанным ниже шагам.
1 шаг. Настраиваем в MS Excel встроенный пакет функций «Пакет анализа».
В программе в MS Excel 2003:
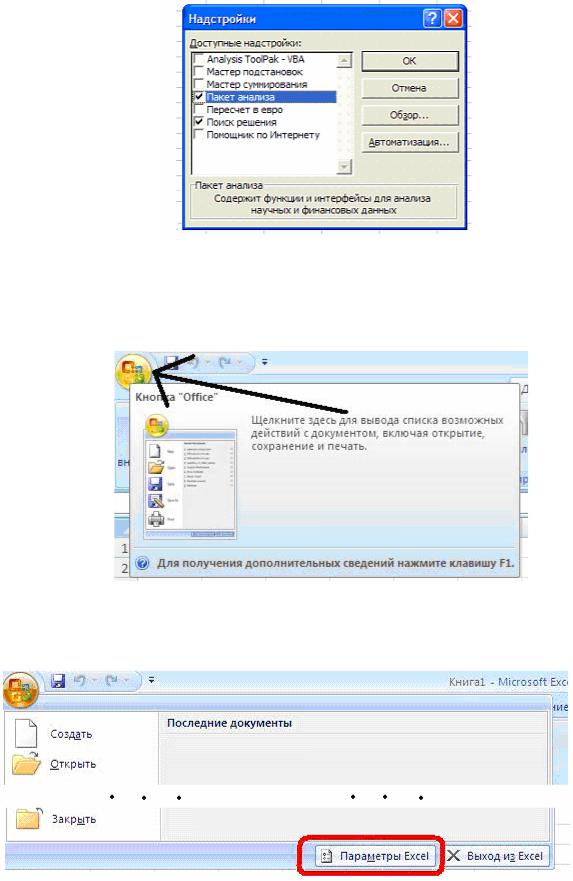
Рис.1.5. Выбор пункта меню «Надстройки» в MS Excel 2003
Выбираем в меню «Сервис» пункт «Надстройки» (рис. 1.5.) и галочкой выделяем строчку «Пакет анализа»2 (рис. 1.6). Нажимаем «ОК», после этого в
2 На всякий случай, можно еще подсветить «Поиск решения» – пригодится для выполнения расчетнографических работ по линейному программированию.
9
«Сервисе» должен появиться пункт «Анализ данных». Если этого не произошло, то закройте MS Excel и откройте его снова.
Рис. 1.6. Выбор пункта меню «Пакет анализа»
В программе в MS Excel 2007:
Действие 1: открываем MS Excel.
Действие 2: нажимаем на желтый круг в левом верхнем углу (рис. ??).
Рис. ??. Желтый круг в левом верхнем углу
Действие 3: в появившемся окне в самом низу нажимаем на кнопку Параметры
Excel (рис. ??).
Рис. ??. Выбираем Параметры Excel
10
