Предположим, что R — отношение между А и B , а S — отношение между В и C. Напомним, что матрица М отношения R определяется условием:

Аналогично заполняется матрица N отношения S

C. Пара (ai,cj) принадлежит композиции отношений (т.е. в матрице P,

просмотреть вcю i – ю строку матрицы M и весь j – й столбец матрицы N и найти в них на одинаковом по порядку месте пару значений И. Если такая пара есть, то (ai ,c j ) S o R и P(i, j) =T . Если же в i – й строке матрицы M нет значений И, соответствующих И на таком же месте в j – м столбце матрицы

N, то P(i,j)=Л.

Таким образом, логическая матрица Р композиции S о R заполняется по следующему правилу:

P(i, j) = (M (i,1) N (1, j)) (M (i,2) N (2, j)) ... (M (i,n) N (n, j))

Для матрицы P пишут P = M × N = M N и она называется булевым произведением матриц.

Пример. Пусть A = {а, b}, B = {1, 2, 3} и С = {x, у}. На этих множествах заданы отношения R A×B и S B ×C

R = {(a,l),(a,2),(a,3),{(b,2)} и S = {(1, у), (2, х), (3, х)}.

Отношение R между A = {а, b} и B = {1, 2, 3} задается матрицей

Аналогично, S — отношение между B и С, задается матрицей

Логическая матрица Р отношения S о R будет содержать две строки (два элемента множества A) и два столбца (два элемента множества C).

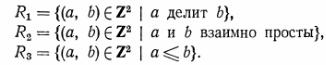
Для определения элемента P11 просматриваем 1 – ю строку и 1 – й столбец

матриц, определяя в них на одинаковом месте символ T. У нас есть, например, элемент 2 B для которого (a,2) R и (2, x) S . Следовательно,

(a, x) S o R и P11 =T . По – другому

P11 = (T F ) (T T ) (T T )= F T T =T

Аналогично

P12 =(T T ) (T F ) (T F )=T F F =T

P21 = (F F ) (T T ) (F T )= F T F =T

P22 =(F T ) (T F ) (F F )= F F F = F

В результате

□

3.3 Отношения эквивалентности

Важную роль в математике играет один специальный класс отношений — отношения эквивалентности. Отношение R на А есть отношение эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Точнее, отношение R на множестве А называется отношением эквивалентности, если оно обладает следующими свойствами: 1) a R a для любого a A (рефлексивность); 2) если a R b, то b R a (симметричность); 3) если a R b и b R c, то a R c (транзитивность). Это отношение часто обозначают символом ~.

Пусть А = {1,2,3,4,5,6} и задано отношение R R={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,2),(1,4),

(2,1),(2,4),(3,5),(5,3),(4,1),(4,2)},

В примере 1 предыдущего параграфа мы установили, что это отношение R на А, рефлексивно, транзитивно и симметрично, поэтому R есть отношение эквивалентности на множестве А. Пусть

Очевидно, R2 есть отношение эквивалентности на множестве Z, но R1 и R3 таковыми не являются.

поскольку 7 − 2 =5 =5 1, и (−11,4) R , так как −11 − 4 = −15 =5 (−3).

Отношение R рефлексивно. Если а — целое число (т.е. a A), то a − a =0 =5 0, так что (a,a) R .

Поскольку R рефлексивно, симметрично и транзитивно, оно является отношением эквивалентности.

□

Если множество А представлено тем или иным способом как объединение своих попарно непересекающихся подмножеств, то говорят о его разбиении, а входящие в это разбиение подмножества называют классами разбиения. Например, множество точек плоскости можно разбить на прямые, параллельные оси х; множество целых чисел разбивается на классы, состоящие из чисел, дающих один и тот же остаток при делении на фиксированное натуральное число n. В первом случае имеем бесконечное семейство классов, во втором случае классов разбиения будет ровно n.

подмножества, элементы которых эквивалентны друг другу и не эквивалентны элементам других подмножеств.

Например, пусть множество А — это набор разноцветных шаров, а отношение R задается условием: (a,b) R тогда и только тогда, когда а и b имеют одинаковый цвет. Поскольку R — отношение эквивалентности (проверьте это), каждый класс эквивалентности будет состоять из шаров, имеющих одинаковый цвет. Если определить отношение R условием: (a,b) R тогда и только тогда, когда шары а и b имеют одинаковый диаметр, то каждый класс эквивалентности будет состоять из шаров одинакового размера.

Докажем, что каждое отношение эквивалентности на множестве А задает некоторое вполне определенное разбиение А. Пусть Ка — класс

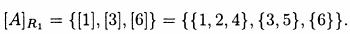
элемент с принадлежит одновременно Ка и Кb, т. е. с ~ а и с ~ b. В силу симметричности а ~ с, и в то же время с ~ b. Используя транзитивность, заключаем, что а ~ b (*). Пусть теперь х — произвольный элемент класса Ка. Тогда х ~ а, и в силу (*) и свойства транзитивности х ~ b, т. е. x Kb . Этим

доказано включение Ka Kb . Точно так же доказывается, что Kb Ka . В

итоге Kb = Ka .

Итак, мы видим, что всякий элемент из А лежит в некотором классе и различные классы не пересекаются. Тем самым получается разбиение множества А на классы эквивалентных элементов.

□

Рассмотрим теперь произвольное разбиение множества А на классы. Два элемента а и b из А будем считать эквивалентными (а ~ b), если они лежат в одном классе. Легко проверяется, что ~ есть отношение эквивалентности на множестве A.

Таким образом, отношение эквивалентности дает универсальный способ разбиения множества на классы, а любое разбиение позволяет

обозначает множество всех классов эквивалентности множества А по отношению R.

Пример. Ранее было показано, что отношение R определенное на множестве

А = {1,2,3,4,5,6}: R={1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,2),(1,4),

(2,1),(2,4),(3,5),(5,3),(4,1),(4,2)}

есть отношение эквивалентности. Классы эквивалентности для каждого элемента A имеют вид:

[1]={1,2,4}

[2]={2,1,4}

[3]={3,5}

[4]={4,1,2}

[5]={5,3}

[6]={6}

Итак, имеется только три различных класса эквивалентности: [1] = [2] =[4] = {1,2,4}, [3]=[5]={3,5}, [6]={6} так, что

□

Этот пример показывает, что, если b [a], то [а] = [b]. На основании этого свойства говорят, что любой элемент класса эквивалентности представляет класс.

Каждый класс эквивалентности содержит, по крайней мере, один элемент, поэтому, в силу рефлексивности отношения, множество всех

элементов, эквивалентных элементу а, должно содержать а. С другой стороны, никакой элемент не может принадлежать двум различным классам эквивалентности.

Пример. Рассмотрим отношение эквивалентности R из примера 1. Для

множества А всех целых чисел R A× A было определено посредством R ={(a,b): a −b =5 k для k Z}. Поскольку

[a] ={x : (x,a) R} ={x : x R a} =

получаем, что множества

[0]={...,−15,−10,−5,0,5,10,15,20,25,...} =[−5] =[0] =[5] =[10] =...

[1]={...,−14,−9,−4,1,6,11,16,...} =[−9] =[−4] =[1] =[6] =...

[2]={...,−13,−8,−3,2,7,12,17,...} =[−8] =[−3] =[2] =[7] =...

[3]={...,−12,−7,−2,3,8,13,18,...} =[−7] =[−2] =[3] =[8] =...

[4]={...,−11,−6,−1,4,9,14,19,...} =[−6] =[−1] =[4] =[9] =...

представляют собой различные классы эквивалентности по отношению R. Таким образом,

[ A]R ={[0], [1], [2], [3], [4]}.

Элементы класса [0] «похожи» в том смысле, что каждый из них кратен пяти. Элементы любого другого класса эквивалентности также «похожи» в том смысле, что имеют один и тот же остаток при делении на пять. □

Упражнения.

Упражнения к п. 3.1

5. Пусть даны отношения

8. Выпишите упорядоченные пары, принадлежащие бинарным отношениям на множествах A={1,3,5,7} и B={2,4,6}. Выпишите матрицы,

представляющие эти отношения.

(a) U ={(x, y): x + y =9} (б) V ={(x, y): x < y}

Ответ:

.

Матрица отношения R в случае (б) имеет вид:

9. Отношение R на множестве А = {1, 2, 3, 4} представлено графом на рисунке. Перечислите упорядоченные пары, принадлежащие R, выпишите соответствующую матрицу и определите это отношение с помощью предикатов.

Решение. В терминах упорядоченных пар R={(2,1),(3,2),(4,3)}. Матрица (относительно данного в условии порядка элементов множества) имеет вид:

с помощью предикатов данное отношение может быть описано как x − y =1.

Упражнения к п. 3.2.

1. Пусть A={а,b,c}, B={4,5,6} и С={x,у,z}. На этих множествах заданы отношения R A×B и S B ×C

R = {(a,4),(a,6),(b,3),(b,5),(c,6)}

и

S = {(4,у),(5,х),(6,х),(6,z)}.

Постройте матрицу композиции отношений S o R .

Упражнения к п. 3.3.