Статистическое изучение вариаций
Вариация (лат.) колеблемость или различия.
Вариация в статистике– это различие в значениях какого-либо признака у разных единиц совокупности в один и тот же период или момент времени.
Средняя величина, как обобщающая характеристика признака не показывает строение совокупности, то есть не дает представления о том, как отдельные значения изучаемого признака отклоняются от среднего (насколько близко примыкают или насколько далеко).
Показателей вариаций пять:
1. Размах вариации – R
2. Среднее линейное отклонение – (d̅)
3. Дисперсия – Ơ2
4. Среднее квадратическое отклонение – Ơ
5. Коэффициент вариаций – V
1. Размах вариации R– это разность между максимальном и минимальном значении признака
R= Хmах – Хmin
где Хmах – наибольшее значение признака
Хmin – наименьшее значение признаков
2. Среднее линейное отклонение (d̅)
Бывает двух видов:
а) для не сгруппированных признаков среднее линейное отклонение выглядит так:
d̅ = ∑| х - х̅ |
n
где n – число ряда
б) для сгруппированных признаков
d̅ взв = ∑| х - х̅ | f
∑ f
где ∑ f –сумма частот вариационного ряда распределений
3. Дисперсия (Ơ 2)(Сигма в квадрате)
а) простая (для не сгруппированных признаков)
Ơ2 пр = ∑ (х - х̅ )
n
б) взвешенная (для сгруппированных признаков)
Ơ2 взв = ∑ (х - х̅ )2 f
∑ f
сигма
4. Среднее квадратическое отклонение(Ơ )
_____ ______
Ơпр = √
ơ2 пр;Ơвзв = √
ơ2 взв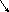
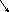
простая взвешенная
Часто возникает необходимость сравнения вариаций различных признаков, например вариация признака возраста, стажа работы и т.д. Для подобных сравнений предыдущие показатели не подходят.
Это может сделать только относительный показатель – это показатель Коэффициент вариаций.
5. Коэффициент вариаций (V) (%)
V= Ơ × 100
х
где Ơ – среднее квадратичное отклонение
х – средняя арифметическая
При V≤ 33% средняя считается типичной надежной
Совокупность считается количественно однородной, если коэф. вариаций не превышает 33% , то есть меньше или равно 33%. Среднее является типичной или надежной.
Если коэф. вариаций больше 40% - это говорит о большой колеблемости признака и следовательно средней мы не может доверять, средняя не является надежной для анализа.
Пример расчета показателей вариации
По данным ряда распределения 60 сотрудников фирмы по стажу работы, необходимо рассчитать показатели вариации.
|
Стаж работы, лет х |
Количество сотруников, чел. f |
Расчетные значения | ||
|
| х - х̅ | (| х – 3,9| ) |
| х - х̅ | f
|
(х - х̅ )2 f | ||
|
2 |
8 |
1,9 |
15,2 |
28,88 |
|
3 |
16 |
0,9 |
14,4 |
12,96 |
|
4 |
17 |
0,1 |
1,7 |
0,17 |
|
5 |
12 |
1,1 |
13,2 |
14,52 |
|
6 |
7 |
2,1 |
14,7 |
30,87 |
|
Итого |
60 |
- |
59,2 |
87,4 |
сумма лет чел Средняя арифметическая
взвешенная
х̅ взв = ∑хf = 2×8 + 3×16 + 4×17 + 5×12 + 6×7 = 3,9 года
∑f 60
чел.
сумма чел
1) Размах вариаций (мах – мin годы) =R = Хmах – Хmin= 6-2 = 4 года
2) Среднее линейное отклонение взвешенное
d̅
взв = ∑ | х - х̅ | f
= |2-3,9|×8+|3–3,9|×16+|4–3,9|×17+|5–3,9|×12+|6–3,9|×7
=15,2+14,4+1,7+13,2+14,7=
∑f 60 60
=59,2 = 0,987 Прямая скобка – мода – то же, что и круглая, но знак минус не учитывается
60
3) Ơ2пр = ∑ | х - х̅ | f = 87,4 = 1,46
∑f 60
1,92×8=28,88 1,12×12=14,52
0,92×16=12,96 2,12×7=30,87
0,12×17=0,17 всего: 87,4
___ _____
4) Ơ = √ Ơ2 = √ 1,46 = 1,21
5) V= Ơ × 100 = 1,21 ×100 =31%
х 3,9
Среднее арифметическое число типично (не превышает)