*** Доп. Элементы дифференциальной

ГЕОМЕТРИИ

1.

Кудрявцев (I) §24 № 1(1,2), 2, 5, 11(3), 12(1,2,3,4),13.20,21,27,48,51,52,76(3),77(1),78(1), 109(1), 110(1), 118,122,123,124(1,2).

1.Построить годографы вектор-функций(tR):

1) x = cost, y = sint, z =1; 2) x = sint, y = cost, z = t²;

2.Доказать,что годограф вектор-функциилежит на сфере.

5.Доказать,что вектор-функцияявляется бесконечно малой при t0.

30

11.Найти производную вектор-функциии написать уравнение касательной в произвольной точке её годографа, если:

3)

12.Найти производные функций:

1) 2)

3) 4)

13.Доказать,что если длина векторовпостоянна в окрестности точкии существует производная от,то векторыиортогональны. Каков механический смысл этого факта.

20.Доказать: еслипостоянные,то: 1) ; 2) .

21.Доказать,что если ,гдепостоянные,то.

27.Доказать,что годограф вектор-функции

, ,где постоянные векторы, причем ине коллинеарны, является эллипсом.

48.Найти уравнение касательной прямой и нормальной плоскости к кривой:в произвольной ее точке.

51.Найти нормальную плоскость к кривойz = x² + y², y = xперпендикулярную к прямой x = y = z.

52.Найти касательную к кривойx²+ y² =10, y²+z² =25в точке(1, 3, 4).

76 (3).Найти кривизну и радиус кривизны в произвольной точке кривой

77 (1).Найти кривизну и центр кривизны в произвольной точке кривой

78 (1).Найти кривизну эллипсаx=acost,y=bsint,

31

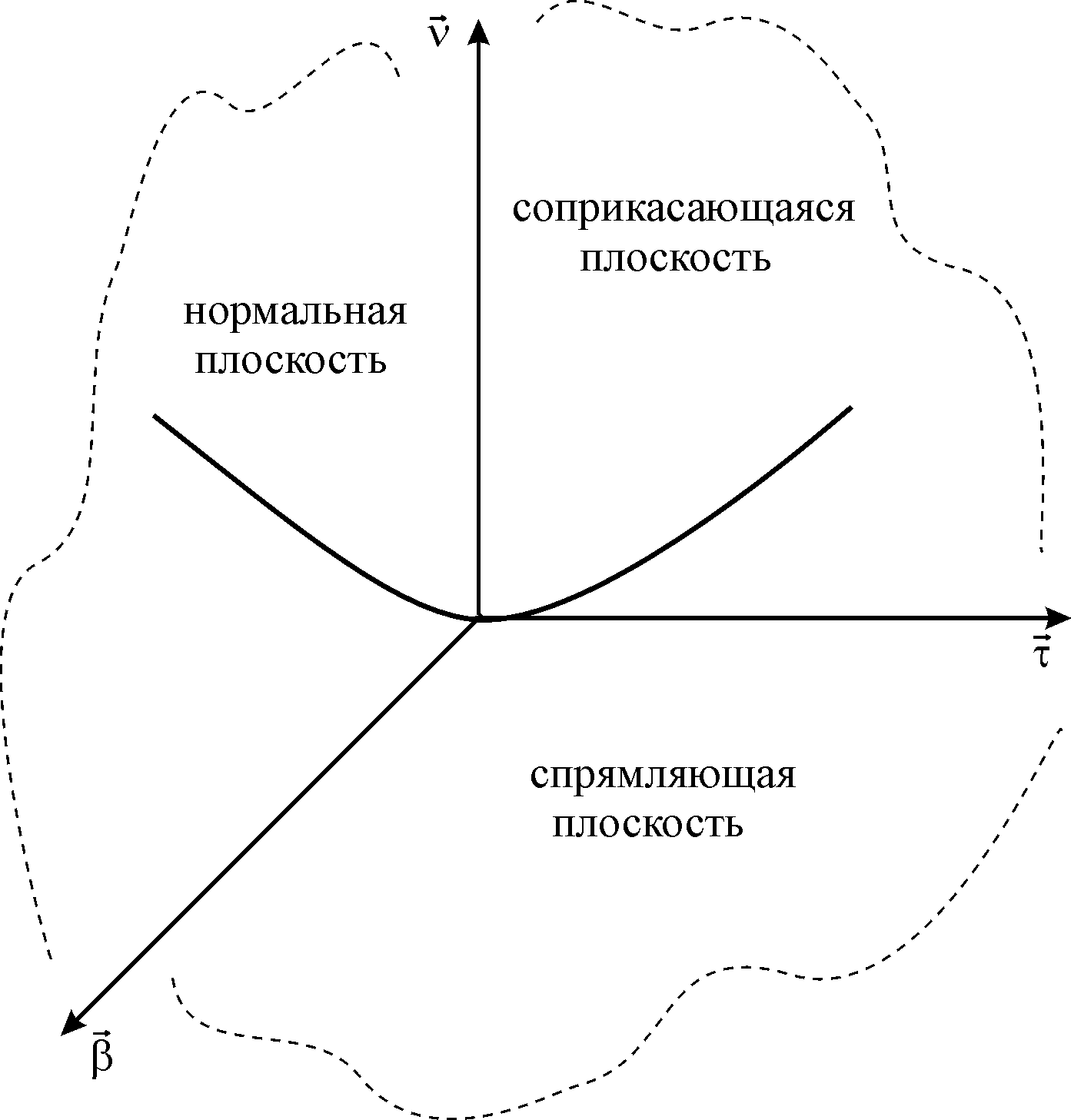
109 (1).Написать уравнение соприкасающейся, нормальной и спрямляющей плоскости в произвольной точке кривой: x = acost, y = asint, z = bt (цилиндрическая спираль).

110 (1). Найти уравнение главной нормали и бинормали к кривой x = a cost, y = a sint, z = bt.

118.Найти векторыкривойx = t sint, y = t cost, z = ye^tвначале координат.

122.Найти кривизну кривой:

1) x = acht, y = asht, z = bt; 2)x = lncost, y =lnsint, z = t; 3) .

123.Найти кручение кривой:

1) x = e^tcost, у =e^tsint, z = e^t; 2)x = achtcost, y = achtsint, z = at; 3)y² =x, x² = z.

124.Найти кривизну и кручение кривой:

1) 2ay = x², 6a²z = x³; 2) x = acht, y = asht, z = at;

***Дополнение.

Основные формулы.

Плоские кривые:

Касательная: .

Нормаль: .

Центр кривизны: .

Кривизна: .

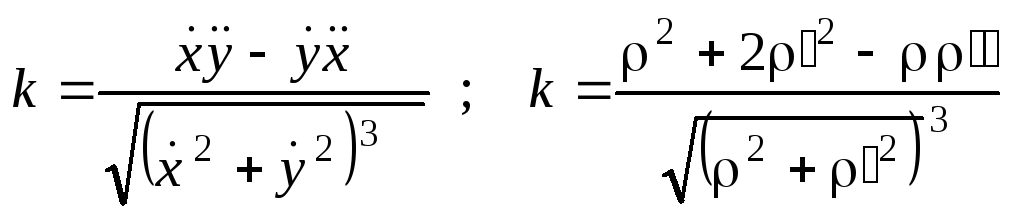Радиус кривизны: .

Пространственные кривые

; .

касател. главн. нормаль бинормаль

32

;

кривизна кручение

; .

Уравнения нормальной, спрямляющей и соприкасающейся плоскости.

Центр кривизны: .

(дифференцирование по S).

ææ(Формулы Френе-Серре).

Отметим, что:

1. Касательная вращается вокруг мгновенного положения бинормали с положительной угловой скоростью k(кривизна).

2. Бинормаль вращается вокруг мгновенного положения касательной с положительной угловой скоростью æ (кручение).

3. Трехгранник Френе вращается вокруг мгновенной оси

æс угловой скоростью(полная кривизна)

4. Разложение ускорения движущейся точки на нормальное и тангенциальное

5. Если , то уравнение эволюты к кривой, заданной этим уравнением будет:, а уравнение эвольвенты к точке кривой будет:.

6. Если кривая L₁является эволютой кL, то криваяLявляется эвольвентой кL₁.

33