Бесконечные произведения
1.
Демидович 30(51,52,56,58,60,61,66,73,74,89,90).
Доказать равенства: 3051. .
3052.
.3056.
.
3058.
.
3060.
.
3061.Доказать
сходимость и определить значение
бесконечного произведения
.
Исследовать сходимость бесконечных произведений:
3066.
.3073.
.3074.
.
Исследовать на абсолютную и условную сходимость бесконечные произведения
3089.
.3090.
.
*** Дополнение.
;
.
При
:
– (ф-ла Валлиса).
Def:
сходится,
если существует, конечен и не равен
нулю
.
12
*) Если
и
,
то произведение называют расходящимся
к нулю;
*) Если
и
,
то произведение называют сходящимся
к нулю или «нулевым» бесконечным
произведением;
*)
~
(бесконечное произведение и ряд сходятся
или расходятся одновременно).
11
*) Необходимое условие сходимости бесконечного произведения:
;
*) Если
(
не меняет знак), то следующее бесконечное
произведение и ряды сходятся или
расходятся одновременно:
~
;
*) Если
иun
меняет знак, а ряды
и
сходятся, то сходится и произведение
;
*)
называют абсолютно или условно сходящимся
при соответствующей сходимости ряда
;
*) Необходимым и
достаточным условием абсолютной
сходимости бесконечного произведения
является абсолютная сходимость ряда
.
13
Эйлеровы интегралы.
1.
Демидович. 38(43,44,45,46,47,48,51,52,56,57,59,61,68).
С помощью эйлеровых интегралов, вычислить:
3843.
.3844.
.3845.
.3846 .
.3847.
.3848.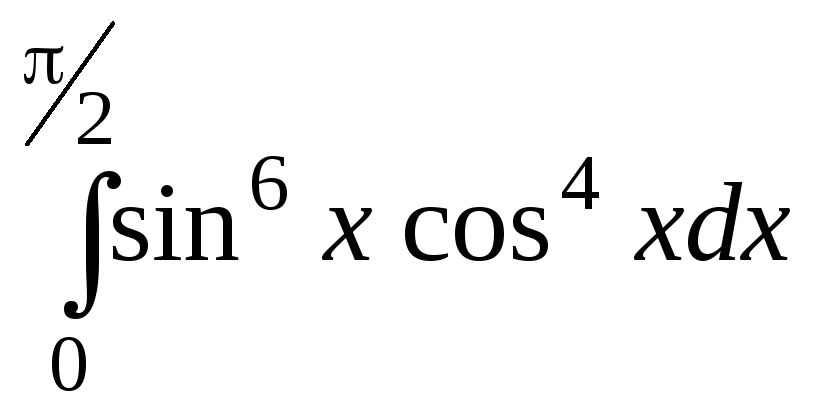
.
Определить область существования и выразить через эйлеровы следующие интегралы:
3851.
(n>0).3852.
.
3856.
.3857.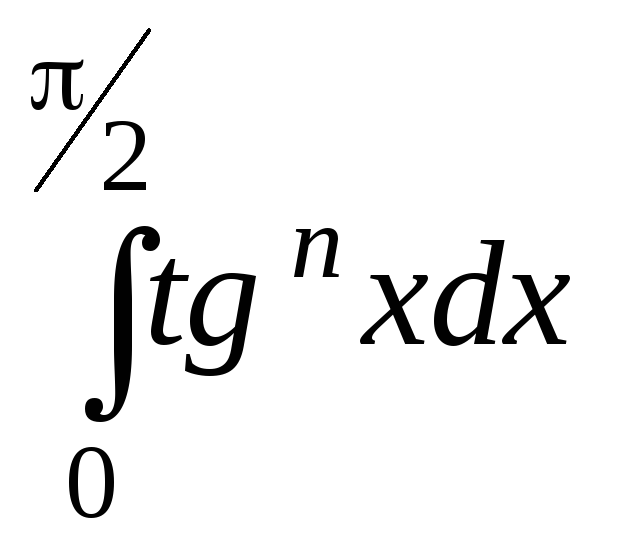
.3859.
(n > 0).3861.
.3868.
.
*** Дополнение
n! =
(формула Стирлинга);
Г(x)
=
(Гамма–функция);
B(x,y) =
(Бета–функция);
B(x,y) =
;
Г(x+ 1) =xГ(x); Г(n)
= (n– 1)!;
Г(x)Г(1 –x)=
;
Г
;
Г
.
14
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
1.
Демидович 31(59, 88, 89,*), 32(28,83,85), 33(07,22,25).
3159.Построить
линии уровня функции
.
Найти двойные пределы:
3188.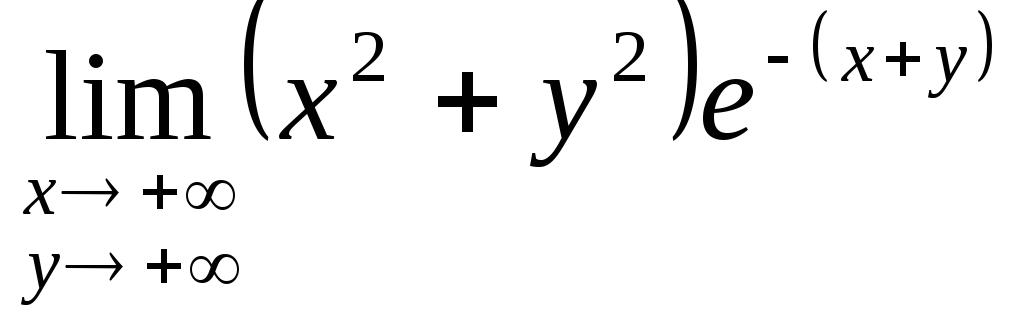
.3189.
.
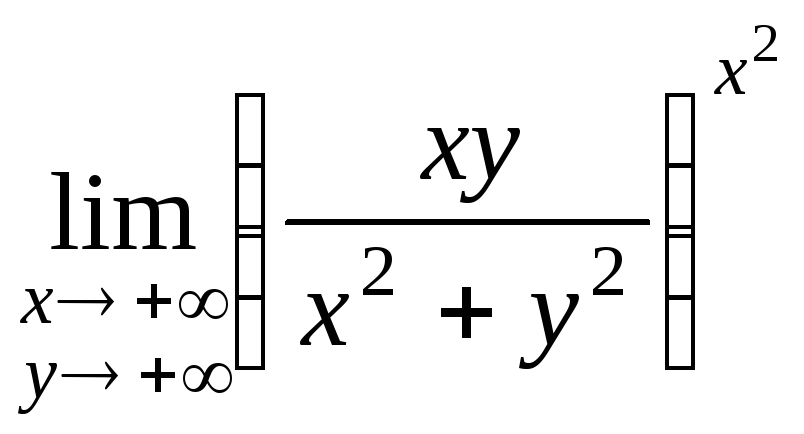*).Найти первые и вторые частные производные функции
.
3228.Найти
частные производные первого и второго
порядка
.
Найти первые и вторые частные производные от следующих функций
3283.
.3285.
.
3307.Найти
,если 
.
Проверить равенства
3322.
,где
.
3325.
,где
.
2.
Демидович 32(36,37,40,45,*,71,75,88,90,95,98).
Найти дифференциалы первого и второго порядка для функций:
3236.
.3237.
.3240.
.
3245.Заменяя приращение функции дифференциалом приближенно вычислить:
15
а)
,
б)
,
в)
,
г)
,
д)
.
*).Найти
первый дифференциал функции
.
Найти дифференциалы указанного порядка
3271.
,
.3275.
,
.
Найти дифференциалы
первого и второго порядка(
– независимые переменные)
3288.
.3290.
.
3295.
,
.3298.
.
3.
Демидович 33(21,26,55,58,85,95,96), 34(01,02,*,07.1,07.2,*).
Проверить равенства:
3321л.
,
где
.
3326.
,
где
.
3355л.Найти
,если
.
3358л.Найти
решение
уравнения
,удовлетворяющее условию
.
3385л.Для
функции
найти частные производные первого и
второго порядка:
.
3395.Найти
,если 
.
16
3396.Найти
и
,если
.
3401.Найти
и
,если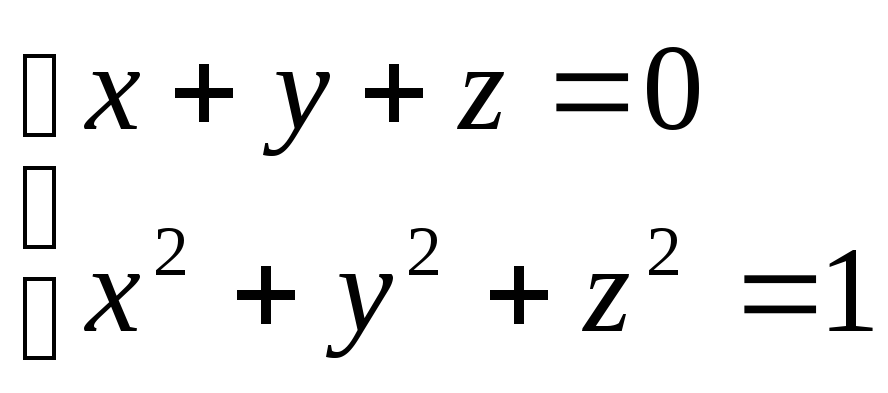
.
3402.Найти
,если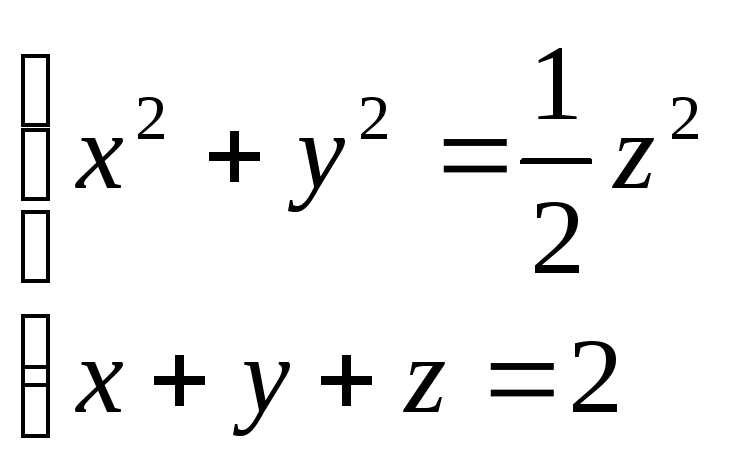 
.
*).Найти
и
,если
.
3407.1.Найти
и
,в точке
если:
.
3407.2.Найти
,если
.
*).Найти
,если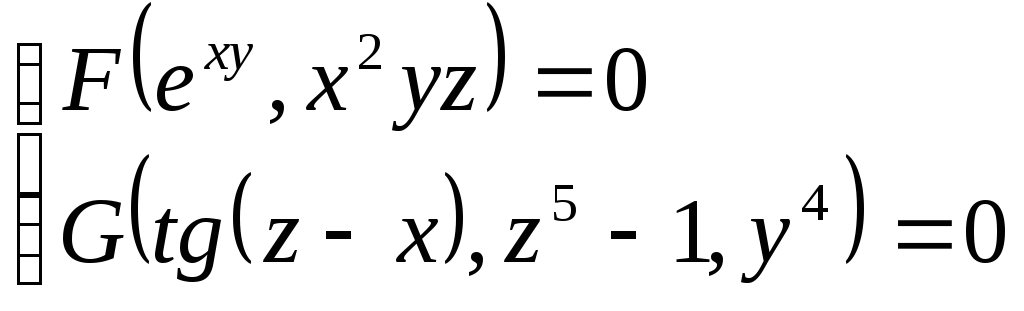 
.
4.
Демидович 34(81,82,83,89,95), 35(13,15,*).
Перейти к полярным координатам в следующих выражениях:
3481.
.3482.
.
3483.
.
Сделать замену независимых переменных:
3489.
,
.
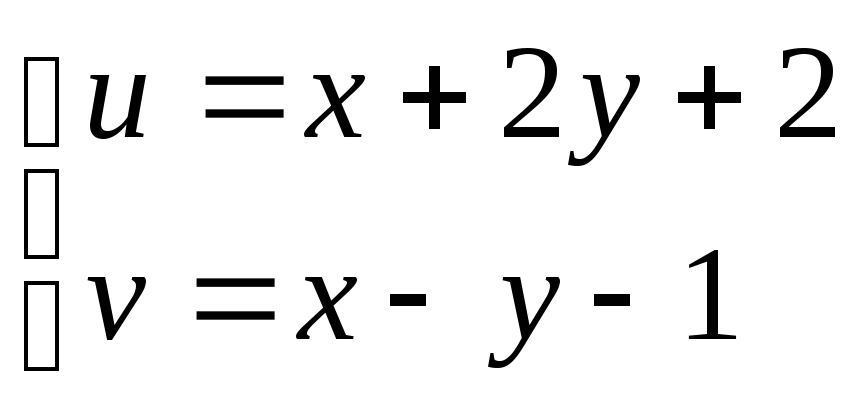17
Сделать замену переменных:
3495.
,если 
.
3513.Сделать
замену переменных в уравнении(
):
,
где 
.
3515.
,если
.
*).В указанном уравнении сделать замену переменных и полученное уравнение решить
;замена: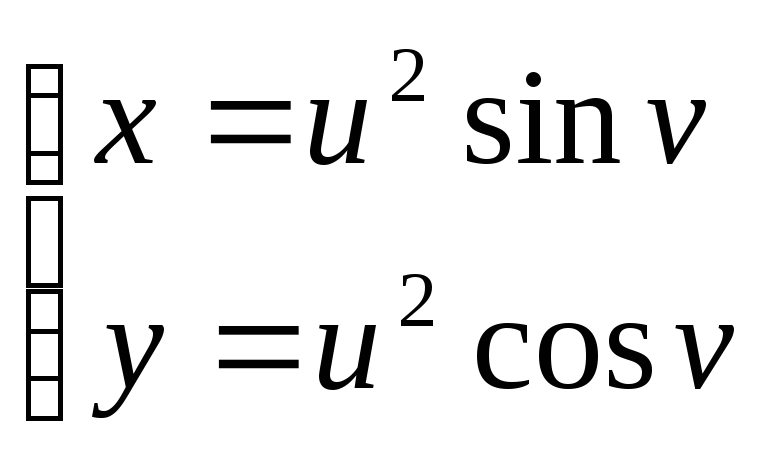
.
5.
Демидович *, 35(82,86,87(б),88,94,95,96), 3602.
В окрестности указанных точек разложить в ряд Тейлора следующие функции:
*).
,
.
3582.
,
.
3586.Разложить по формуле Маклорена функцию
до
членов 4-го порядка включительно.
3587(б).С
точностью до членов второго порядка
получить приближенную формулу для
,
если
3588.Упростить
выражение
,
считая
малыми по абсолютной величине.
Разложить в ряд Маклорена:
3594.
.3595.
.
3596.
.
18
3602.Функцию
разложить в степенной ряд по целым
положительным степеням биномов
и
.
6.
Демидович. 36(24,25,27,33,45*,48,51,55,57.1,77,78).
Исследовать на экстремум функции
3624.
.3625.
.3627.
.3633.
.
3645*.
3648.
.
3651.Найти
экстремум
,если
.
Исследовать функции на условный экстремум:
3655.
,
если
.
3657.1.
,если
.
Найти наибольшее и наименьшее значение функции
в области 
3678.
,если