
- •Ориентировочный план занятий
- •Определенные интегралы
- •Найти неопределенные интегралы:
- •Несобственные интегралы
- •Бесконечные произведения
- •Доказать равенства: 3051. .
- •Исследовать сходимость бесконечных произведений:
- •Эйлеровы интегралы.
- •Двойные и тройные интегралы
- •Криволинейные и поверхностные интегралы. Элементы теории поля.
- •*** Доп. Элементы дифференциальной
- •Кудрявцев (I) §24 № 1(1,2), 2, 5, 11(3), 12(1,2,3,4),13.20,21,27,48,51,52,76(3),77(1),78(1), 109(1), 110(1), 118,122,123,124(1,2).
- •Пространственные кривые
- •Экзаменационные вопросы по курсу
- •Первый курс. Второй семестр
Найти неопределенные интегралы:
2304.![]() .2305.
.2305. ![]() (x≥ 0).
(x≥ 0).
2306.![]()
![]() .
.
Вычислить определенные интегралы от ограниченных разрывных функций:
2309.![]() .2310.
.2310.![]() .
.
4.
Демидович. 23(16,17,18, *,*,21,24,25,26.1).
Определить знаки следующих определенных интегралов
2316. а)![]() .
б)
.
б)![]() .
в)
.
в)![]() .
г)
.
г)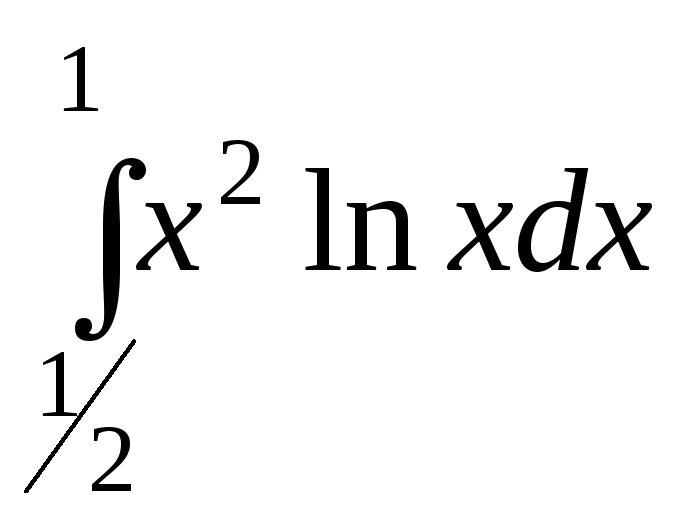 .
.
2317.Какой из двух интегралов больше:
а)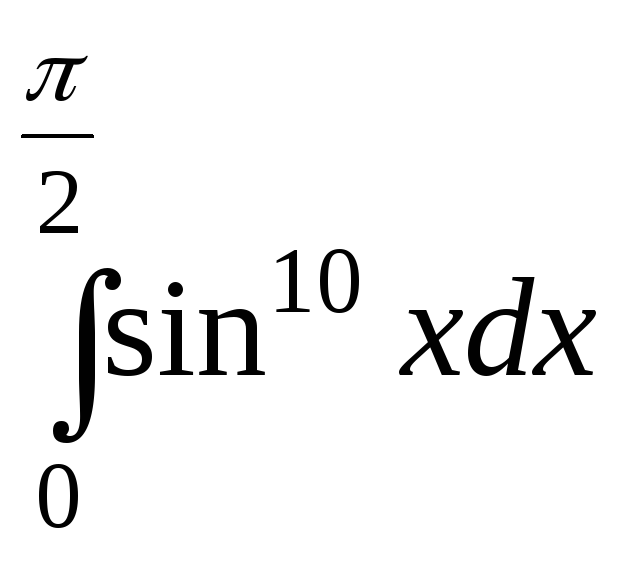 или
или 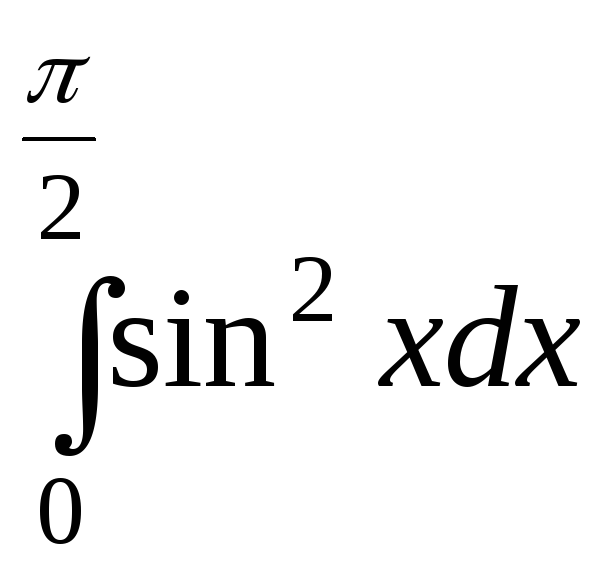 ;
б)
;
б)![]() или
или![]() ;
;
в)![]() или
или![]() .
.
5
2318.Определить средние значения функций на промежутках
а)
![]() на
на![]() ;
в)
;
в)![]() на
на![]() ;
;
б)
![]() на
на![]() ;
г)
;
г)![]() на
на![]() .
.
*).Найти среднее значение функцииy= sinx,еслиx![]()
*)л.Применяя первую теорему о среднем
оценить:![]() .
.
2321.Сила
переменного тока меняется по закону
![]() ,
где
,
где![]() - амплитуда, t – время, Т – период,
- амплитуда, t – время, Т – период,![]() - начальная фаза. Найти среднее значение
квадрата силы тока.
- начальная фаза. Найти среднее значение
квадрата силы тока.
Пользуясь первой теоремой о среднем оценить интегралы:
2324.![]() .2325.
.2325.![]()
2326.1.Найти:
а)![]() ,
б)
,
б)![]() ,
,![]() .
.
5.
Демидович. 23(28,29,98) 24(01,03,16,20,11).
Пользуясь второй теоремой о среднем оценить интегралы:
2328.![]() .2329.
.2329.![]() .
.
Найти площади фигур, ограниченных кривыми:
2398.y=x2,x+y = 2.
2401.y=x, y =x+ sin2x(0≤х≤π)
Найти площади фигур, ограниченных кривыми:
2403.![]() .2416.
.2416.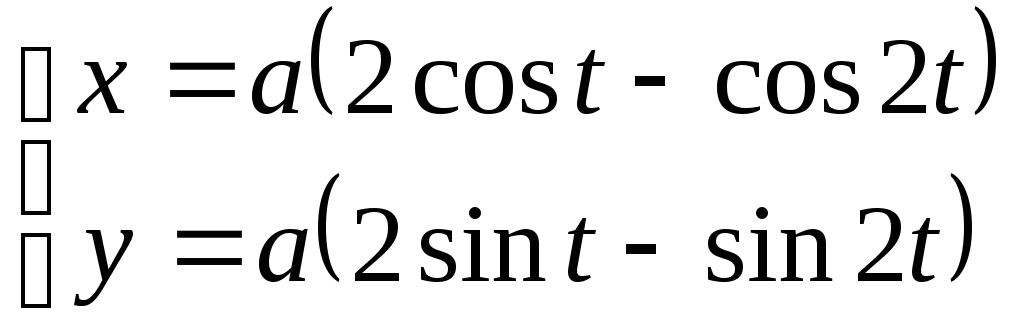 .
.
2420.![]() (трилистник).
(трилистник).
2411.В каком отношении парабола y2 =2x делит площадь круга
x2+y2 =8.
6
6.
Демидович. *, 24(15,20,21,34,42,62,63, 65).
Найти площади фигур, ограниченных кривыми:
*). x = acost, y = bsint.
2415. x = a(cost + tsint), y = a(sint – tcost) (0 ≤ t ≤ 2π) (развертка круга) и x = a, y≤ 0.
2420.
![]() .2421.
.2421.![]() ;
;![]() ,
,![]() .
.
2434.Найти длину дуги кривой:y=eх(0 ≤х≤х0).
2442.Найти
длину дуги следующей кривой![]() ,
,![]() .
.
Найти объемы тел, ограниченных поверхностями
2462.![]() ;
;![]() ,
,![]() .2465л.
.2465л.![]() ,
,
![]() .
.
2463.Найти объёмтела, ограниченного поверхностью:
![]() .
.
7.
Демидович. 2497, 25(02,03,10,13,23,25,28).
2497.Найти
площадь поверхности вращения образованной
вращением кривой
![]() вокруг полярной оси.
вокруг полярной оси.
2502.Найти статический момент и момент инерции однородной треугольной пластинки с основанием b и высотой h относительно основания (плотностьρ = 1).
2503.Найти
моменты инерции однородной эллиптической
пластинки с полуосями а и b
относительно ее главных осей
![]() .
.
2510. Определить центр тяжести однородного полушара радиуса а.
2513.Определить координаты центра тяжести
области, ограниченной первой аркой
циклоиды
![]() ,
,![]()
![]() и осьюОх.
и осьюОх.
7
2523.Однородный шар радиуса R и плотности
![]() вращается вокруг своего диаметра с
угловой скоростью
вращается вокруг своего диаметра с
угловой скоростью![]() .
Определить кинетическую энергию шара.
.
Определить кинетическую энергию шара.
2525.Определить, с какой силой притягивает
круглая пластинка радиуса а и постоянной
поверхностной плотности
![]() материальную точку Р массы т, находящуюся
на перпендикуляре к плоскости пластинки,
проходящем через ее центр Q на кратчайшем
расстоянии PQ, равном b.
материальную точку Р массы т, находящуюся
на перпендикуляре к плоскости пластинки,
проходящем через ее центр Q на кратчайшем
расстоянии PQ, равном b.
2528.Скорость
распада радия в каждый момент времени
пропорциональна его наличному количеству.
Найти закон распада радия, если в
начальный момент t= 0 имелось
![]() граммов радия, и через время Т=1600лет
его количество уменьшится в два раза.
граммов радия, и через время Т=1600лет
его количество уменьшится в два раза.
Несобственные интегралы
1.
Демидович. 23(35,38,42,46,48,50,53,58,59).
Вычислить интегралы:
2335.
![]() .2338.
.2338.![]() .
.
2342.![]() .2346.
.2346.![]()
![]() .
.
С помощью формул понижения вычислить следующие несобственные интегралы:
2348.![]() .2350.
.2350.![]() .
.
2353.
а)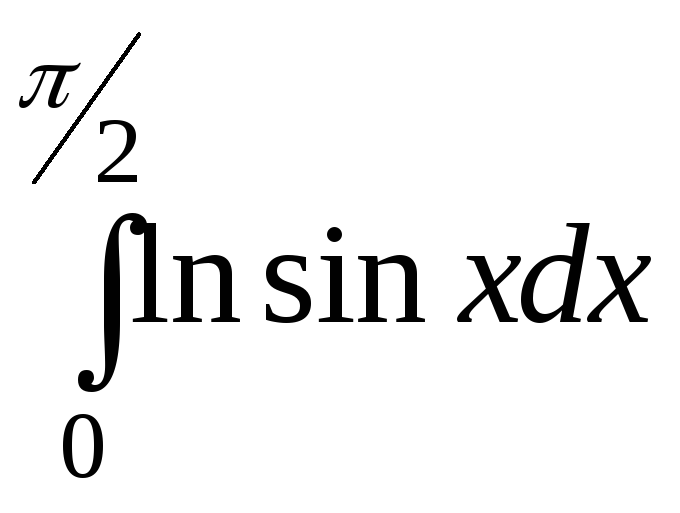 ,
б)
,
б)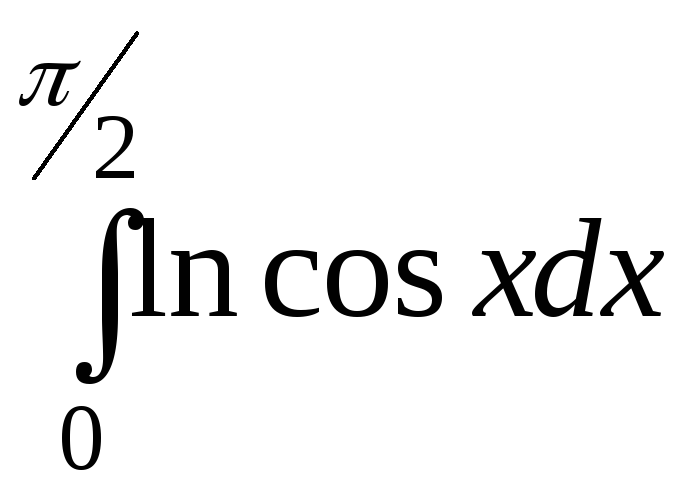 .
.
Исследовать интегралы на сходимость
2358.![]() .2359.
.2359.![]() .
.
8
2.
Демидович. 23(60,61,62,63,68,69,70,72,74)
Исследовать сходимость интегралов:
2360.![]() .2361.
.2361.![]() .2362.
.2362.![]() .
.
2363.![]() ,
,![]() .2368.
.2368.![]() .2369.
.2369.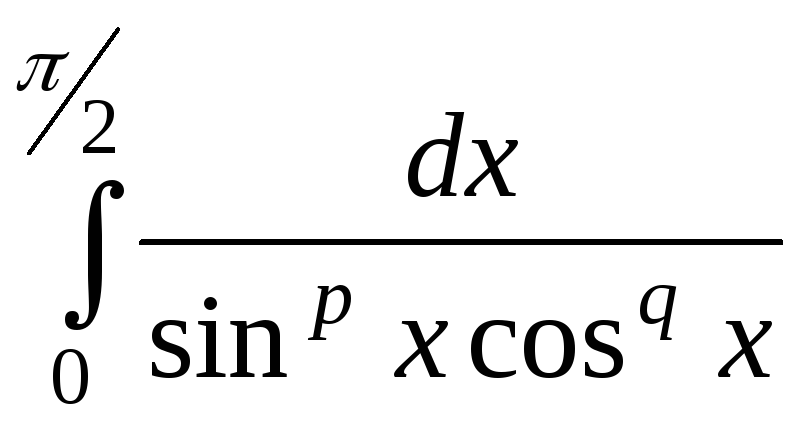 .2370.
.2370.![]() .2372.
.2372.![]() .2374.
.2374.![]() .
.
3.
Демидович. 23(78,79,80,80.1,80.2,81,84,92,*,*)
2378.![]() .2379.
.2379.![]() .2380.
.2380.![]() .
. 2380.1.
.
. 2380.1.![]() .2380.2.
.2380.2.![]() .2381.
.2381.![]() .2384.Если
.2384.Если ![]() сходится, то обязательно ли
сходится, то обязательно ли ![]() при
при![]() .
.
Рассмотреть
примеры: а)![]() ,
б)
,
б)![]() .
.
2392.Найти v.p.![]() .
.
При каких
значениях параметров
![]() и
и![]() сходятся интегралы, а при каких
расходятся:*)
сходятся интегралы, а при каких
расходятся:*)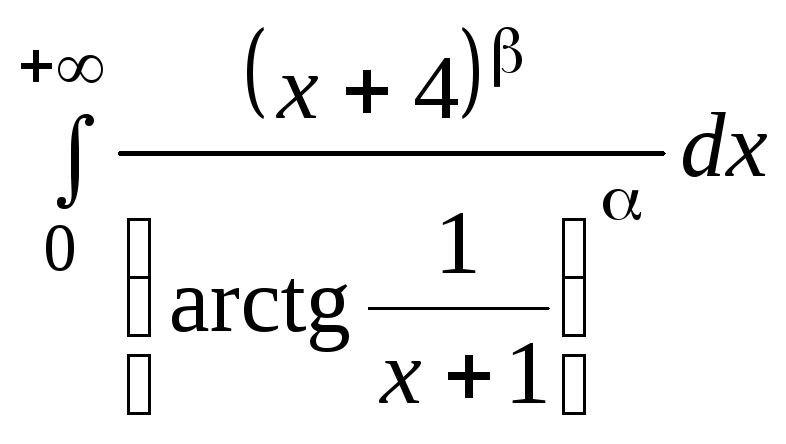 .*)
.*)![]() .
.
9
РЯДЫ
1.
Демидович. 25(74,76,78,79,80,83,84,86,89.2), 2626.
2574.Пользуясь критерием Коши доказать сходимость ряда
![]()
2576.Пользуясь критерием Коши доказать расходимость ряда
![]()
Пользуясь признаками Даламбера, Коши и сравнения исследовать сходимость рядов
2578.![]()
2579.![]()
2580.
![]() .
.
Исследовать сходимость рядов
2583.
![]() .
.
2584.![]() .
.
2586.![]() .
2589.2.
.
2589.2.![]() .
.
2626.![]() .
.
Для заметок:
10
2.
Демидович.26(33,34,38,42,67,68,69,71,73.1,75).
Исследовать сходимость рядов:
2633.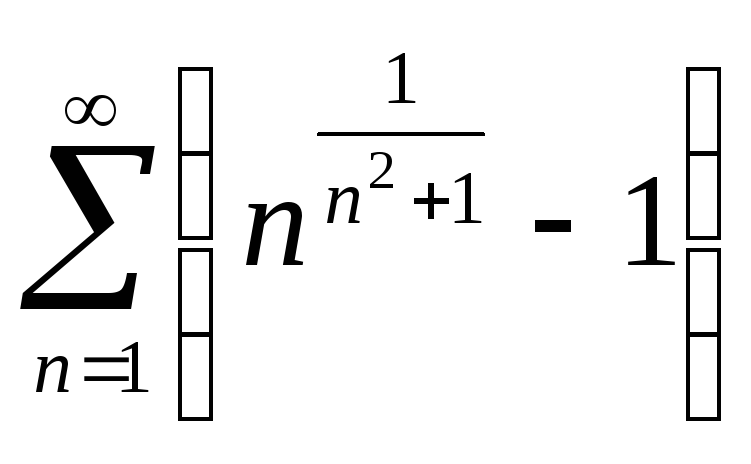 .2634.
.2634.![]() .2638.
.2638.![]() .
.
2642.![]() .
.
Исследовать сходимость знакопеременных рядов:
2667.![]() .2668.
.2668.
![]() .
.
2669.![]() .2671.
.2671.![]() .
.
2673.1.![]() .2675.
.2675.
![]() .
.
3.
Демидович. 27(16,17,18,20,21,22,23,25,26,28,31).
Определить области абсолютной и условной сходимости рядов :
2716.![]() .2717.
.2717.![]() .2718.
.2718.![]() .
.
2720.![]() .2721.
.2721.![]() .2722.
.2722.![]() .
.
2723.![]()
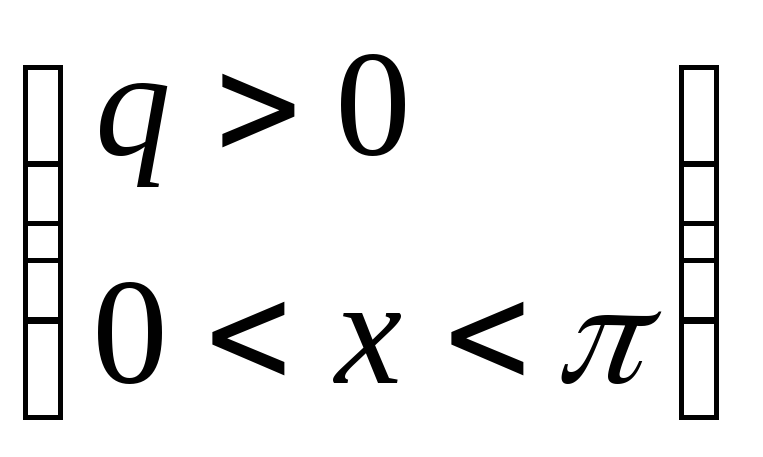 .2725.
.2725.![]() .
.
2726.![]() .2728.
.2728.![]() .2731.
.2731.![]() .
.
11
