
5
.pdf
Центр дистанционного обучения
Процессы и аппараты химической технологии
Лекция №5
ФИО преподавателя: Таран Юлия Александровна
e-mail: taran_yu@mirea.ru
Online-edu.mirea.ru
1 online.mirea.ru
Центр дистанционного обучения
Теория гидродинамического подобия
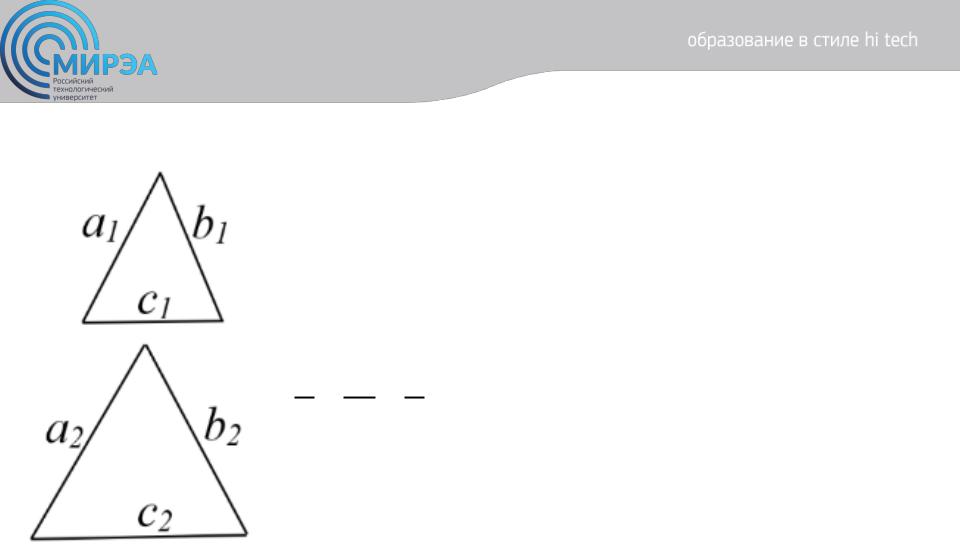
Геометрическое подобие предполагает пропорциональность сходственных размеров, т. е. между соответствующими линейными размерами существует постоянное соотношение (см. рис. 16).
а1 = 1≠ = 1 = – множитель подобия по длине.
а2 2 2
Рисунок 16. К установлению геометрического подобия
2 online.mirea.ru
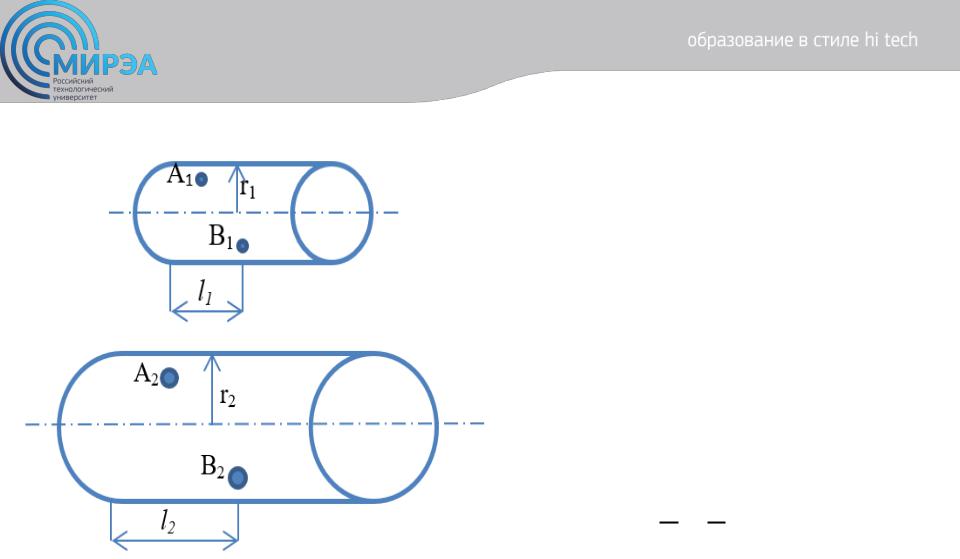
Рисунок 17. Подобные течения в каналах: малый – модель; большой – образец
Центр дистанционного обучения
В курсе ПАХТ используется
физическое подобие применительно к переносу различных субстанций. Два физических явления подобны, если в
сходственных точках геометрически подобных систем одноименные характеристики различаются только постоянными коэффициентами (множителями подобия). Математические описания подобных систем идентичны.
Отношение 1 = 1 = = г является
2 2
множителем геометрического подобия, постоянным для любой пары сходственных точек в этих каналах.
3 online.mirea.ru
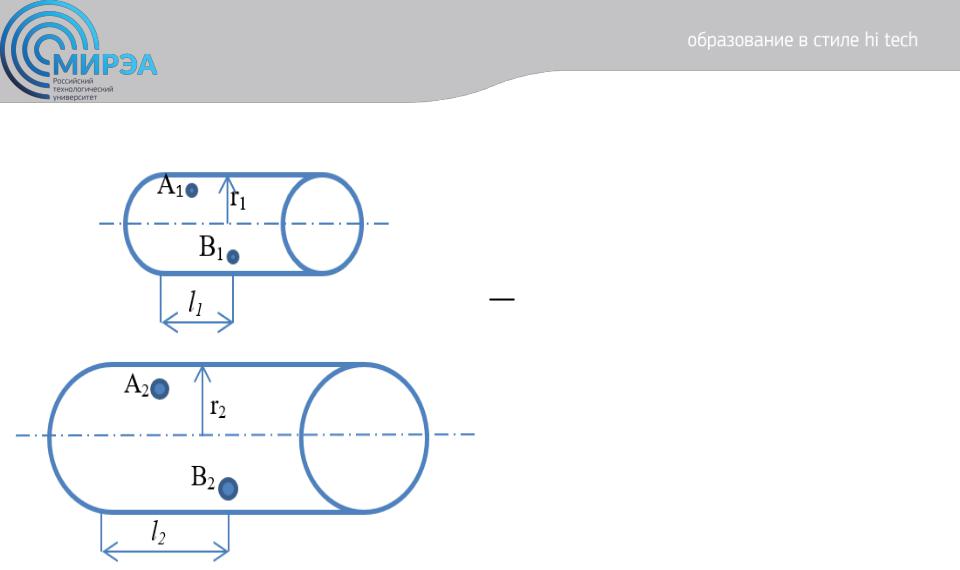
Рисунок 17. Подобные течения в каналах: малый – модель; большой – образец
Центр дистанционного обучения
По определению физического подобия как для пары точек А1 и А2, так и для B1 и В2 характерны равенства:
|
|
= |
1 |
; |
|
= |
р1 |
; = |
1 |
; |
|
= |
1 |
; |
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
р2 |
|
2 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
=1 ,2
причем mi – множители подобия (масштабные множители), разные для разных характеристик
( |
|
≠ |
|
≠ ≠ ), но одинаковые в |
|
|
|
|
|
||
пределах |
одной |
характеристики для каждой |
|||
пары сходственных точек, т. е. при переходе от одной пары сходственных точек к другой значения , , , … не изменяются. Таким образом каждый множитель подобия выступает
вкачестве масштабной характеристики
соответствующей физической величины.
4 online.mirea.ru
Центр дистанционного обучения
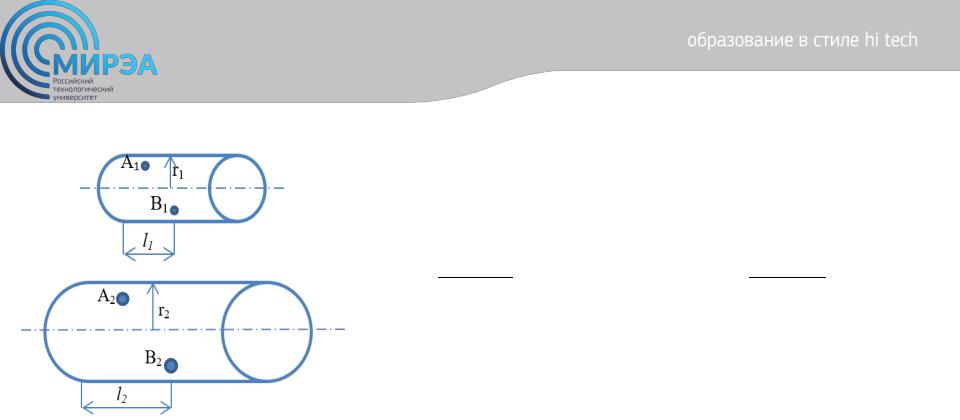
Обозначим принадлежность к модели или образцу индексами 1 и 2:
|
Уравнение неразрывности |
Уравнение неразрывности для |
|||||||
для модели: |
|
образца: |
|
|
|
||||
|
1 |
+ (1 1) |
+ = 0 |
|
2 |
|
+ |
(2 2) |
+ = 0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
1 |
1 |
|
2 |
|
|
2 |
|
||
Рисунок 17. Подобные течения в каналах: малый – модель; большой – образец
5 online.mirea.ru
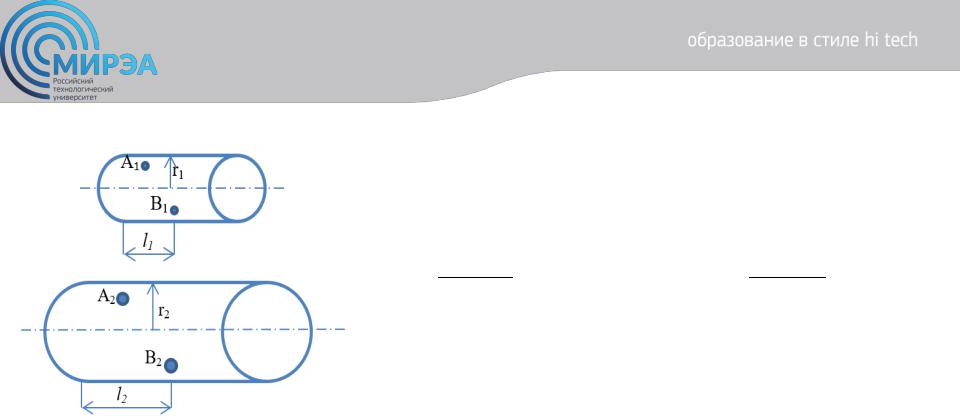
Центр дистанционного обучения
Рисунок 17. Подобные течения в каналах: малый – модель; большой – образец
Обозначим принадлежность к модели или образцу индексами 1 и 2:
|
Уравнение неразрывности |
Уравнение неразрывности для |
|||||||||||||||||||
для модели: |
|
|
|
|
|
|
|
|
образца: |
|
|
|
|
|
|||||||
|
1 |
+ (1 1) |
+ = 0 |
|
|
|
|
2 |
|
+ (2 2) + = 0 |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
||||
|
Применим к данным уравнениям масштабные |
||||||||||||||||||||
преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
1 |
|
; |
|
= |
1 |
; |
|
= |
1 |
; |
|
= |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6 online.mirea.ru
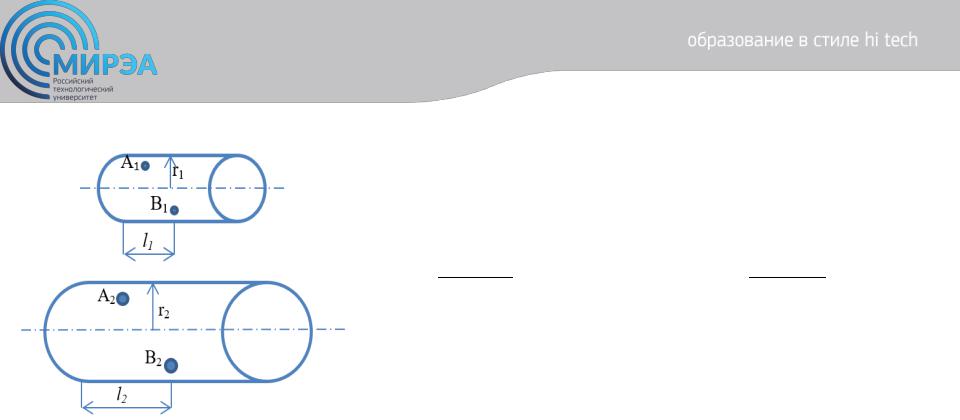
Центр дистанционного обучения
Рисунок 17. Подобные течения в каналах: малый – модель; большой – образец
Обозначим принадлежность к модели или образцу индексами 1 и 2:
|
Уравнение неразрывности |
Уравнение неразрывности для |
||||||||||||||||||||||
для модели: |
|
|
|
|
|
|
|
|
образца: |
|
|
|
|
|
|
|
||||||||
|
1 |
+ |
(1 1) |
+ = 0 |
|
|
|
|
2 |
|
+ (2 2) |
+ = 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
|
Применим к данным уравнениям масштабные |
|||||||||||||||||||||||
преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
1 |
; |
|
= |
1 |
; |
|
= |
1 |
|
; |
|
= |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= ; = |
|
; = |
|
; = , |
|||||||||||||||||||
1 |
|
2 |
1 |
|
|
2 |
|
1 |
|
|
|
|
2 |
1 |
|
|
2 |
|||||||
причём множитель подобия для координат ml
общий для всех координат ( 1 и 2, 1 и 2, 1 и 2) и линейных размеров (l1 и l2).
7 online.mirea.ru

Центр дистанционного обучения
|
Уравнение неразрывности |
Уравнение неразрывности для |
|||||||
для модели: |
|
образца: |
|
|
|
||||
|
1 |
+ (1 1) |
+ = 0 |
|
2 |
|
+ |
(2 2) |
+ = 0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
1 |
1 |
|
2 |
|
|
2 |
|
||
Применим к данным уравнениям масштабные преобразования:
= |
1 |
; |
|
= |
1 |
; |
|
= |
1 |
; |
|
= |
1 |
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
2 |
|
|
2 |
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= ; = |
|
; = |
|
; = , |
|||||||||||||||
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
|
|
|
2 1 |
|
2 |
||||
причём множитель |
подобия |
для |
координат |
ml |
общий |
для всех координат |
|||||||||||||
( 1 и 2, 1 и 2, 1 и 2) и линейных размеров (l1 и l2).
Подставив эти выражения в уравнение для модели и вынеся постоянные множители за знак производных, имеем
|
|
|
|
|
|
|
|
|
( |
) |
|
|||
|
|
|
2 |
+ |
|
|
|
|
2 |
2 |
|
+ = 0. |
||
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
8 online.mirea.ru

Центр дистанционного обучения
Подставив эти выражения в уравнение для модели и вынеся постоянные множители за знак производных, имеем
|
|
|
|
|
|
|
|
|
( |
) |
|
|||
|
|
|
2 |
+ |
|
|
|
|
2 |
2 |
|
+ = 0. |
||
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
Полученное уравнение для модели и уравнение для образца по определению физического подобия должны быть идентичны. Это возможно, если комплексы
содержащие множители подобия и сокращаются, т. е. являются равными
9 online.mirea.ru

Центр дистанционного обучения
Подставив эти выражения в уравнение для модели и вынеся постоянные множители за знак производных, имеем
|
|
|
|
|
|
|
|
|
( |
) |
|
|||
|
|
|
2 |
+ |
|
|
|
|
2 |
2 |
|
+ = 0. |
||
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
Полученное уравнение для модели и уравнение для образца по определению физического подобия должны быть идентичны. Это возможно, если комплексы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
содержащие множители подобия |
|
и |
|
|
|
сокращаются, т. е. являются равными |
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
= |
|
|
или |
|
= |
|
. |
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
10 online.mirea.ru
