
7
.pdf
Центр дистанционного обучения
Процессы и аппараты химической технологии
Лекция №7
ФИО преподавателя: Таран Юлия Александровна
e-mail: taran_yu@mirea.ru
Online-edu.mirea.ru
1 online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
2online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
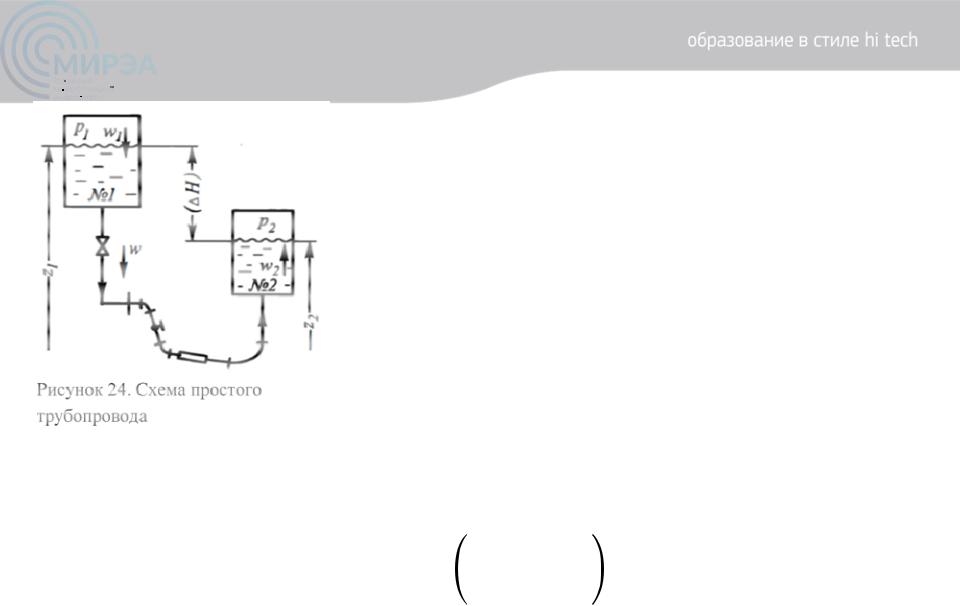
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
п. |
|
2 |
|
2 |
3online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
п. |
|
2 |
|
2 |
Следует иметь в виду, что скоростные напоры в резервуарах на уровне свободных
поверхностей и пренебрежимо малы по сравнению с другими составляющими уравнения и их можно опустить. Это связано с тем, что сечения резервуаров много больше сечения трубопровода, а значит скорости течения в резервуарах много меньше скорости в трубопроводе.
4online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
п. |
|
2 |
|
2 |
Учитывая вышесказанное, можно записать:
п
5online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
п. |
||
|
|
2 |
|
|
2 |
||||||
Учитывая вышесказанное, можно записать:
п
Левая часть равенства представляет собой
располагаемый напор, состоящий из разности геометрических высот и разности давлений в сосудах, выраженных в метрах столба протекающей жидкости, и обозначается ∆.
Отсюда
∆ п.
6online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
п. |
||
|
|
2 |
|
|
2 |
||||||
Учитывая вышесказанное, можно записать:
п ∆ п.
Потери напора п складываются из сопротивлений движению жидкости на прямых участках трубопровода и на местных сопротивлениях. Тогда суммарное сопротивление течению жидкости равно:
|
|
|
|
|
|
|
|
||
п |
г |
|
2 |
вх 2 |
з 2 |
д 2 |
кр 2 |
р 2 |
вых 2 . |
|
|||||||||
7online.mirea.ru
Центр дистанционного обучения
|
|
|
|
|
|
|
|
|
|
|
Расчет простого трубопровода |
||||||
|
|
|
|
Для сечений 1 и 2, совпадающих со |
|||||||||||||
|
|
|
|
свободными |
поверхностями |
в |
сосудах, |
||||||||||
|
|
|
|
может быть записано уравнение Бернулли: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
п. |
|||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
п |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
∆ п. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
п |
г |
|
2 |
вх 2 |
з 2 |
д 2 |
кр 2 |
р 2 |
вых 2 . |
||||||||
|
|||||||||||||||||
В более краткой форме: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
$ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∆ |
г |
|
" # |
2 |
, |
|
|
|
'40* |
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
|
|
где ∑$# # – сумма всех коэффициентов местного сопротивления.
8online.mirea.ru

Центр дистанционного обучения
Расчет простого трубопровода
Для сечений 1 и 2, совпадающих со
свободными поверхностями в сосудах,
может быть записано уравнение Бернулли:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
п. |
||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
п |
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
∆ |
$п. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∆ |
|
г |
|
" # |
|
|
, |
|
||||||||||
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
Откуда |
|
|
|
скорость |
в |
|
трубе |
w равна: |
|||||||||||
|
$ |
|
|
∆, |
|
|
|
|
|
|
|
|
|
|
|
'41* |
|||
- |
. |
0∑$1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
г |
/ |
$ |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
9online.mirea.ru
Центр дистанционного обучения
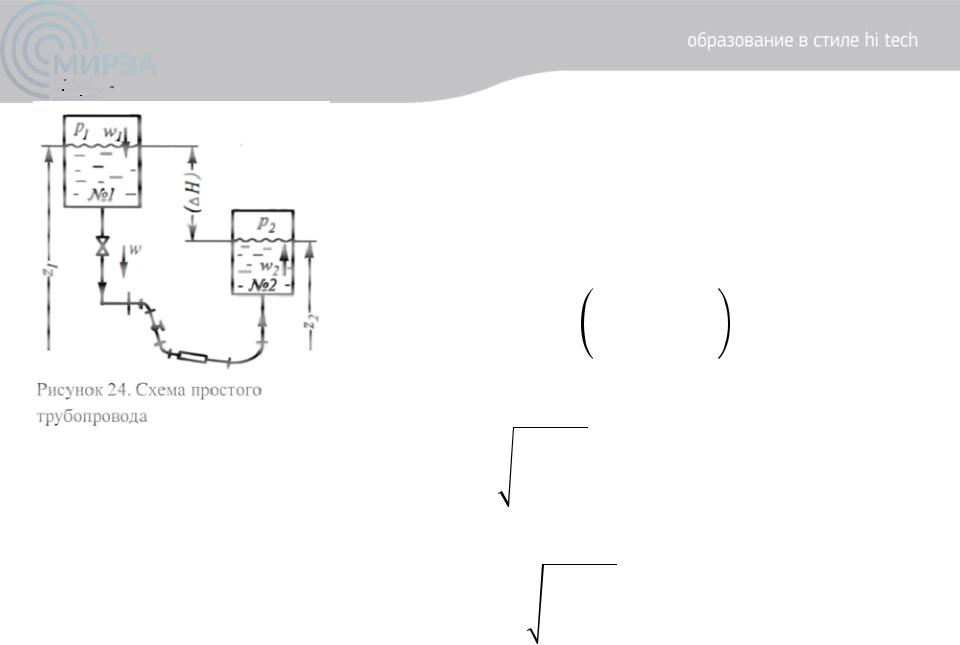
Расчет простого трубопровода
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
п. |
|||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
п |
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
п. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
$ |
|
|
|
|
|||||||
|
|
∆ |
|
|
|
|
г |
|
|
" # |
2 , |
|
||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
Откуда |
скорость |
в |
|
трубе |
w равна: |
|||||||||||||||||
|
$ |
|
|
∆, |
|
|
|
|
|
|
|
'41* |
||||||||||
|
- |
. |
0∑$1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
г |
/ |
|
|
$ 2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Объёмный расход жидкости равен: |
||||||||||||||||||||||
V |
45 $ |
|
|
|
∆, |
|
|
|
|
|
|
|
'42* |
|||||||||
6 |
|
|
|
|
-г |
. |
0∑$$12 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
/ |
|
|
|
|
|
|
|||||||||||
10 online.mirea.ru
