
2
.pdf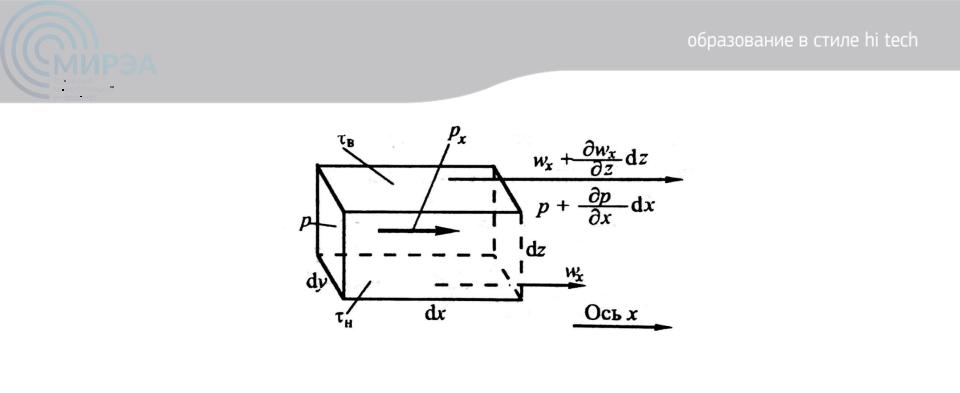
Центр дистанционного обучения
Рисунок 5. К выводу уравнения Навье-Стокса
Тангенциальные поверхностные силы (сдвига, внутреннего трения) рассмотрим для какой-нибудь пары граней, например, вдоль:
-нижней грани dxdy: н , где н – напряжение трения на нижней грани, выражающее перенос импульса из объёма жидкости снизу через грань dxdy в элементарный контур dV, получающий импульс (Прт);
-верхней грани dxdy: в , где в – напряжение трения на верхней грани, выражающее потерю импульса через верхнюю грань dxdy из контура dV в жидкостное пространство (Ухт).
11 online.mirea.ru
Центр дистанционного обучения
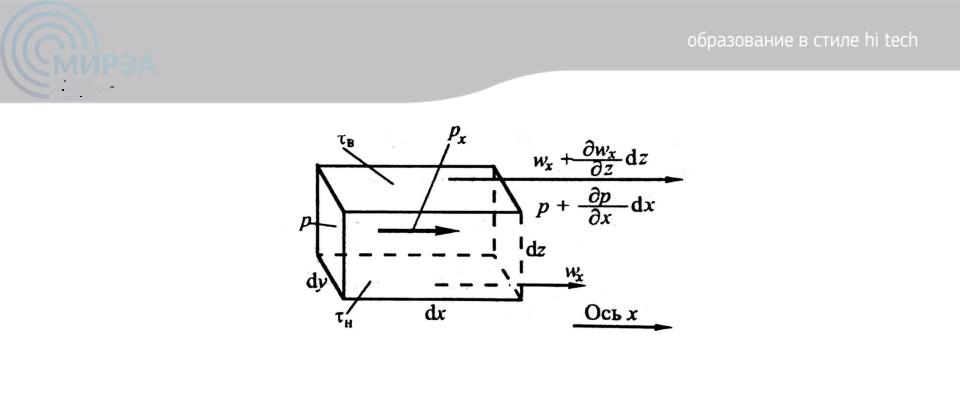
Рисунок 5. К выводу уравнения Навье-Стокса
Тангенциальные поверхностные силы (сдвига, внутреннего трения) рассмотрим для какой-нибудь пары граней, например, вдоль:
- нижней грани dxdy: н , где н – напряжение трения на нижней грани, выражающее перенос импульса из объёма жидкости снизу через грань dxdy в
элементарный контур dV, получающий импульс (Прт); |
|
- верхней грани dxdy: в , где в – напряжение трения на верхней грани, |
|
выражающее потерю импульса через верхнюю грань dxdy из контура dV в |
|
жидкостное пространство (Ухт). |
|
По закону Ньютона: т !( ) , |
|
12 |
online.mirea.ru |

Центр дистанционного обучения
По закону Ньютона: т !( ) ,
тогда в рассматриваемом случае:Прт н !( ,+ .
13 online.mirea.ru

Центр дистанционного обучения
По закону Ньютона: т !( ) ,
тогда в рассматриваемом случае:Прт н !( ,+ .
Поскольку скорость по оси x верхней грани увеличивается на приращение вдоль оси z и
равна |
+ |
, то уход импульса через верхнюю грань равен: |
|
|
||||||||
, |
"- |
|
||||||||||
Ухт |
в !( |
" |
|
" |
!( |
" |
! ( |
. |
||||
" |
" |
" |
"- |
|||||||||
|
|
|
|
|
|
|
|
|||||
14 online.mirea.ru

Центр дистанционного обучения
По закону Ньютона: т !( ) ,
тогда в рассматриваемом случае:Прт н !( ,+ .
Поскольку скорость по оси x верхней грани увеличивается на приращение вдоль оси z и
равна |
+ |
, то уход импульса через верхнюю грань равен: |
|
||||||||||||
, |
|
||||||||||||||
Ухт в |
" |
|
" |
|
|
" |
|
"- |
|
||||||
!( " |
" |
|
!( " |
! ( |
|
|
. |
||||||||
"- |
|||||||||||||||
Соответственно: Прт ! Ухт |
|
верх. и нижн. |
н ! в |
|
"- |
|
|
||||||||
|
|
" |
|
" |
"- |
|
|
|
|
||||||
!( |
" ( |
" ( |
|
|
( |
|
|
V |
|
||||||
|
"- |
"- |
|
||||||||||||
15 online.mirea.ru

Центр дистанционного обучения
По закону Ньютона: т !( ) ,
тогда в рассматриваемом случае:Прт н !( ,+ .
Поскольку скорость по оси x верхней грани увеличивается на приращение вдоль оси z и
равна |
+ |
, то уход импульса через верхнюю грань равен: |
|
||||||||||||
, |
|
||||||||||||||
Ухт в |
" |
|
" |
|
|
" |
|
"- |
|
||||||
!( " |
" |
|
!( " |
! ( |
|
|
. |
||||||||
"- |
|||||||||||||||
Соответственно: Прт ! Ухт |
|
верх. и нижн. |
н ! в |
|
"- |
|
|
||||||||
|
|
" |
|
" |
"- |
|
|
|
|
||||||
!( |
" ( |
" ( |
|
|
( |
|
|
V |
|
||||||
|
"- |
"- |
|
||||||||||||
Для ближней и дальней грани и для левой и правой грани аналогичным образом получим:
Прт ! Ухт |
ближ.и дальн. |
|
( |
6 + |
V; |
||
|
76 |
||||||
Прт ! Ухт |
лев. и прав. |
( |
"- |
V. |
|||
|
"- |
||||||
16 online.mirea.ru

Центр дистанционного обучения
По закону Ньютона: т !( ) ,
тогда в рассматриваемом случае:Прт н !( ,+ .
Поскольку скорость по оси x верхней грани увеличивается на приращение вдоль оси z и
равна |
+ |
, то уход импульса через верхнюю грань равен: |
|
||||||||||||
, |
|
||||||||||||||
Ухт в |
" |
|
" |
|
|
" |
|
"- |
|
||||||
!( " |
" |
|
!( " |
! ( |
|
|
. |
||||||||
"- |
|||||||||||||||
Соответственно: Прт ! Ухт |
|
верх. и нижн. |
н ! в |
|
"- |
|
|
||||||||
|
|
" |
|
" |
"- |
|
|
|
|
||||||
!( |
" ( |
" ( |
|
|
( |
|
|
V |
|
||||||
|
"- |
"- |
|
||||||||||||
Для ближней и дальней грани и для левой и правой грани аналогичным образом получим:
Прт ! Ухт |
ближ.и дальн. |
( |
6 + |
V; |
|
||||||||
76 |
|
||||||||||||
Прт ! Ухт |
лев. и прав. ( |
"- |
|
V. |
|
||||||||
|
"- |
|
|
||||||||||
В целом баланс всех тангенциальных сил: |
|
||||||||||||
Прт ! Ухт ∑ ( |
6 + |
|
6 + |
|
6 + |
; (<- ;. |
|
||||||
6 |
76 |
,6 |
|
||||||||||
|
|
|
|
17 |
online.mirea.ru |
||||||||

Центр дистанционного обучения
На массу жидкости плотностью ρ в объёме dV могут действовать внешние массовые силы (Источники и Стоки).
Ист ! Ст ? V.
18 online.mirea.ru

Центр дистанционного обучения
На массу жидкости плотностью ρ в объёме dV могут действовать внешние массовые силы (Источники и Стоки).
Ист ! Ст ? V.
Равнодействующая всех рассмотренных выше сил обусловит Результат. По II закону Ньютона он равен произведению массы жидкости ? V в контуре dV на ускорение вдоль оси x:
Рез ? V
19 online.mirea.ru

Центр дистанционного обучения
Собирая найденные величины в ОБС, получаем: |
? V. |
||
! |
" |
V (<- V ? V |
|
|
" |
|
|
20online.mirea.ru
