2

Центр дистанционного обучения

Процессы и аппараты химической технологии

Лекция №2

ФИО преподавателя: Таран Юлия Александровна

e-mail: taran_yu@mirea.ru

Online-edu.mirea.ru

1 online.mirea.ru

Центр дистанционного обучения

Дифференциальное уравнение движения несжимаемой жидкости

(уравнение Навье-Стокса)

Главная проблема при изучении движения жидкости – определить давление и скорость в какой-либо точке в произвольной момент времени:

p = p(x; y; z; τ) w = w(x; y; z; τ)

Анализ размерности количества движения (после домножения числителя и знаменателя на секунду) приводит к произведению силы на время:

2online.mirea.ru

Центр дистанционного обучения

Дифференциальное уравнение движения несжимаемой жидкости

(уравнение Навье-Стокса)

Главная проблема при изучении движения жидкости – определить давление и скорость в какой-либо точке в произвольной момент времени:

p = p(x; y; z; τ) w = w(x; y; z; τ)

3online.mirea.ru

Центр дистанционного обучения

Дифференциальное уравнение движения несжимаемой жидкости

(уравнение Навье-Стокса)

Главная проблема при изучении движения жидкости – определить давление и скорость в какой-либо точке в произвольной момент времени:

p = p(x; y; z; τ) w = w(x; y; z; τ)

Анализ размерности количества движения (после домножения числителя и знаменателя на секунду) приводит к произведению силы на время:

4online.mirea.ru

Центр дистанционного обучения

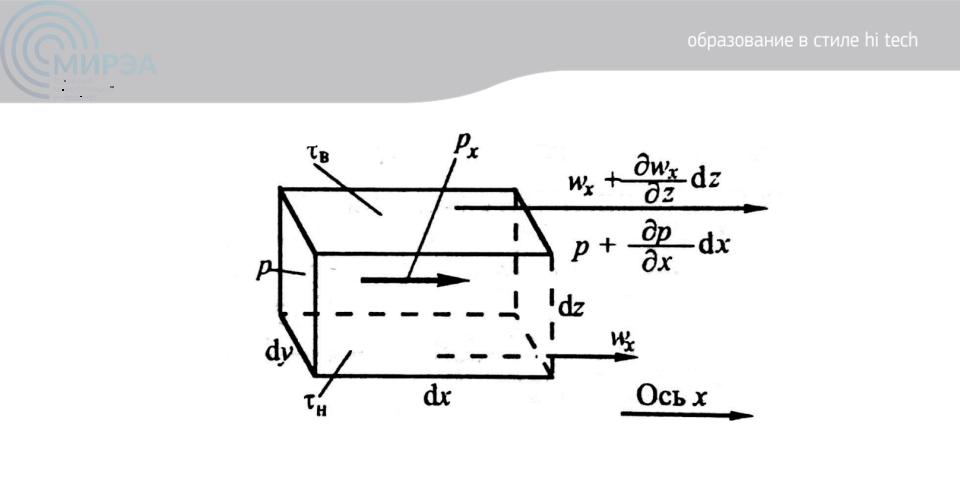
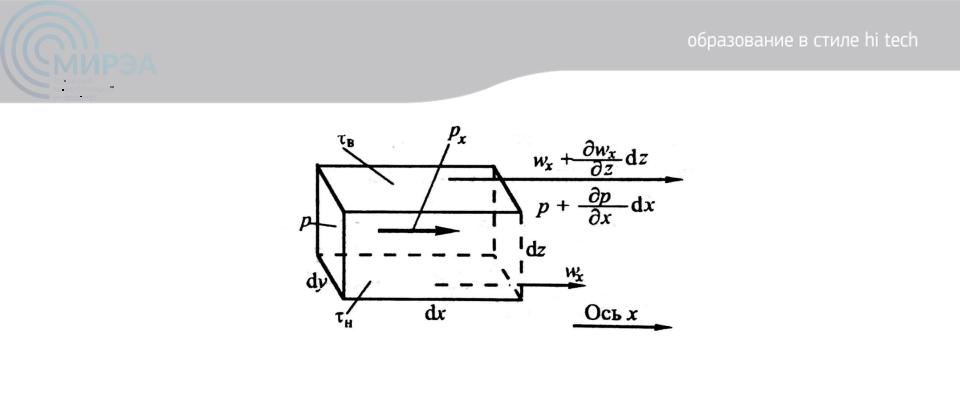
Рисунок 5. К выводу уравнения Навье-Стокса

5online.mirea.ru

Центр дистанционного обучения

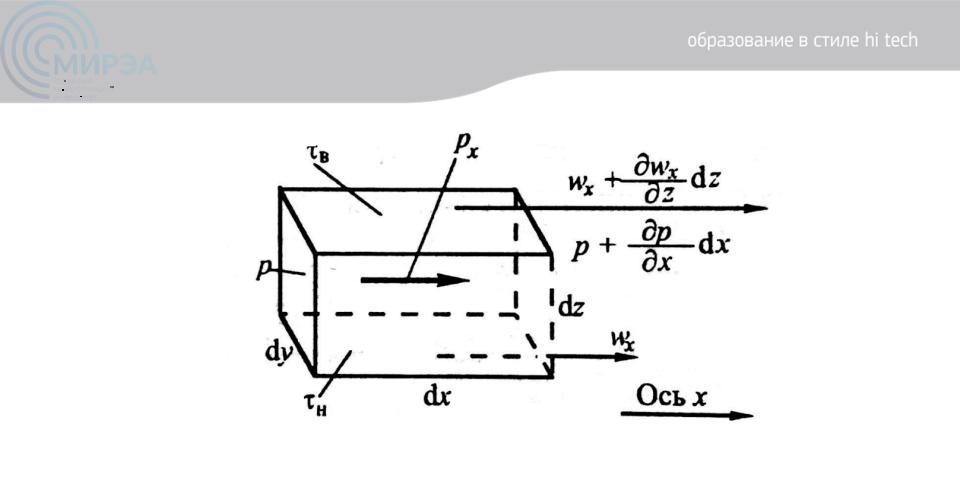
Рисунок 5. К выводу уравнения Навье-Стокса

ОБС:Пр – Ух + Ис – Ст = Нак (Рез)

6online.mirea.ru

Центр дистанционного обучения

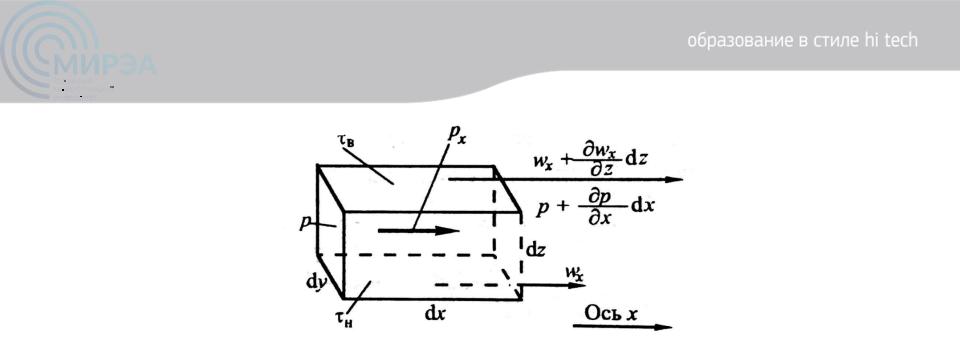
Рисунок 5. К выводу уравнения Навье-Стокса

Нормальные поверхностные силы (силы давления), действующие вдоль оси x:

-на левую грань dydz, где давление p, сила давления равна: pdydz (Приход импульса в контур dV);

7online.mirea.ru

Центр дистанционного обучения

Рисунок 5. К выводу уравнения Навье-Стокса

Нормальные поверхностные силы (силы давления), действующие вдоль оси x:

-на левую грань dydz, где давление p, сила давления равна: pdydz (Приход импульса в контур dV);

- на правую грань, где давление равно , сила давления равна:(Уход импульса из контура dV)

8online.mirea.ru

Центр дистанционного обучения

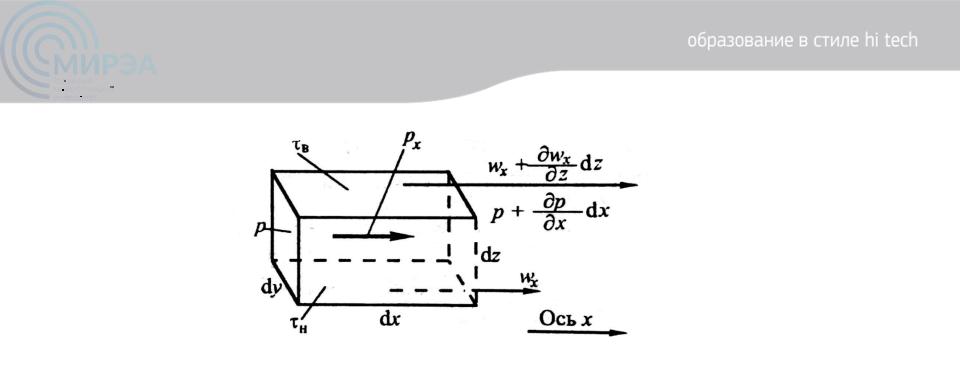
Рисунок 5. К выводу уравнения Навье-Стокса

Нормальные поверхностные силы (силы давления), действующие вдоль оси x:

-на левую грань dydz, где давление p, сила давления равна: pdydz (Приход импульса в контур dV);

Центр дистанционного обучения

Рисунок 5. К выводу уравнения Навье-Стокса

Тангенциальные поверхностные силы (сдвига, внутреннего трения) рассмотрим для какой-нибудь пары граней, например, вдоль:

-нижней грани dxdy: н , где н – напряжение трения на нижней грани, выражающее перенос импульса из объёма жидкости снизу через грань dxdy в элементарный контур dV, получающий импульс (Прт);

10 online.mirea.ru