Обработка результатов эксперимента

Измерения геометрических размеров стержня являются прямыми измерениями, поэтому погрешности величин а,b и L определяются стандартными методами обработки прямых измерений. Прямыми являются и измерения массы. Однако при этом будем считать, что случайная погрешность определения массы много меньше систематической, так что полная погрешность определения массы равна систематической погрешности, составляющей 1г.

Стрела прогиба  определяется косвенным образом по формуле =n₀ –n, где n₀ и n, прямые измерения, производимые по микрометру с точностью 0,01мм. Погрешность  определяется по формуле . Очевидно, чтоn₀=n=0,01мм, так что =0,014мм. Итак, абсолютная погрешность измерения стрелы прогиба во всех опытах будет одинакова и равна 0,014мм.

Согласно формуле (5) существует линейная связь между стрелой прогиба и массой груза, т.е. =Вm. Коэффициент В по данным эксперимента можно было бы определить так. Каждый опыт дает определенное значение B_i:

В_i =  _i / m _i , (7)

где _i и m_i - значения величин  и m, полученные в i-том опыте. Индекс i у величины B показывает, что это значение соответствует i-тому опыту. Из значений B_i можно образовать среднее

. (8)

Здесь следует отметить, что это простой, но не самый лучший способ определения B. В самом деле, m есть величина, характеризующая условия опыта, которую мы знаем практически точно, а  есть результат опыта, известный с погрешностью. Погрешность  одинакова во всех измерениях. Тогда ошибка в величине B, равная _i /m_i, тем больше, чем меньше m_i. Иначе можно сказать, что значение B, вычисленное по формуле (8), не является наилучшей оценкой истинного B. Это является следствием того, что величины B_i неравноточные.

Строго задача о нахождении наилучшей оценки истинного значения B по данным эксперимента и известной зависимости типа Y=aX (в данном случае =Bm) ставится так. Необходимо найти такое значение B, при котором функция =Bm наилучшим образом соответствует опытным данным (смысл нечеткого выражения "наилучшим образом" станет ясным из дальнейшего).

Выберем за меру отклонения функции от экспериментальных данных для i-го опыта величину (_i-Bm_i )². Если бы за меру отклонения была взята просто величина _i-Bm_i, то сумма отклонений в нескольких опытах могла бы оказаться весьма малой за счет взаимного уничтожения отдельных слагаемых большой величины, но имеющих разные знаки. Это, однако, вовсе не говорило бы о том, что функция =Bm хороша. Очевидно, что такого взаимного уничтожения не будет, если мера отклонения выбрана в виде (_i-Bm_i)².

Итак, в качестве меры общего отклонения S в описании опытных данных функцией =Bm необходимо взять сумму мер отклонений для всех опытов, то есть:

. (9)

Таким образом, наша функция будет наилучшим способом описывать опытные данные, если S, то есть сумма квадратов отдельных отклонений, минимальна. Метод определения констант, входящих в формулу, из требования минимальности S, называется методом наименьших квадратов.

Величина S является функцией B, т.е. S=S(B). Чтобы найти такое значение B, которое доставляет минимум функции S (наилучшее значение B), необходимо, как известно, решить уравнение dS/dB=0. Используя (9), получаем:

или ,

что дает . (10)

Итак, подставляя в формулу (10) экспериментальные значения m_i и _i, рассчитывается значение величина, являющееся наилучшей оценкой истинного B. Среднеквадратичное отклонение определяется по формуле:

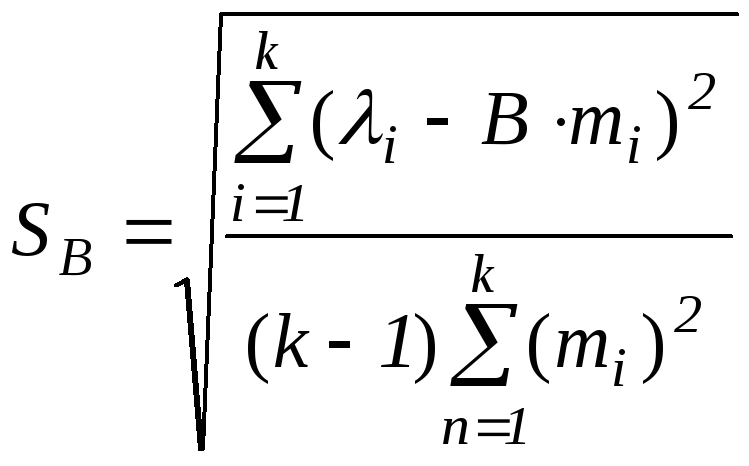. (11)

Для расчета доверительного интервала ^о B выбирается доверительная вероятность  и определяется коэффициент Стьюдента t_,k-1, т.е. для числа на единицу меньше числа проделанных опытов. Тогда, как обычно, ^о B=t_,k-1S_B.

Методом наименьших квадратов следует обработать экспериментальные точки, полученные как при нагружении стержня, так и при его разгрузке. Следует также на экспериментальных графиках провести "наилучшие" прямые, используя значение рассчитанные значения В.

После расчета коэффициента пропорциональности Вможно рассчитать по формуле (6) значение модуля Юнга. Погрешности, входящих в эту формулу величин, известны. Естественно, что значения этих погрешностей определяют и погрешность определения величиныE. ВеличинаEявляется результатом косвенного измерения. ЗначениеEопределяется по формуле погрешности косвенных измерений. Предполагая при этом,g=0, можно записать:

. (12)

Взяв производные и поделив обе части (12) на величину E=gL³/4ab³B, получим выражение, которое удобно использовать для расчета погрешности

. (13)

Подставляя в формулу (6) вначале случайные, а затем систематические погрешности, можно определить соответственно случайную и систематическую(_С Е) погрешности измерения модуля Юнга. Полная погрешность единичного измерения модуля Юнга определяется по формуле.Таким образом, будут получены два значения модуля Юнга (из экспериментов при нагружении и разгрузке стержня). Их надо сравнить друг с другом и с табличными значениями.