
electrodynamics
.pdf§1.Электрическое поле |
|
|
|
|
21 |
|
m = 9,1 10 −31 кг , |
заряд |
электрона e = 1,6 10 −19 Кл , |
гравитационная |
|||
постоянная G = 6,67 10 −11 Н м2 / кг2 . |
|
|
|
|||
1.4. Вычислите |
ускорение |
a , |
сообщаемое |
одним электроном |
другому, |
|
находящемуся от первого на |
расстоянии |
r = 1мм . |
Масса |
электрона |
||
m = 9,1 10 −31 кг , заряд электрона e = 1,6 10 −19 Кл . |
|
|
||||
1.5. Две бесконечно длинные параллельные нити, заряженные с одинаковой линейной плотностью κ = 3 10 −6 Кл/ м , находятся на расстоянии b = 20 мм
друг от друга. Какая сила F действует на единицу длины каждой нити?
1.6. Бесконечная прямая нить, равномерно заряженная с линейной плотностью κ1, и отрезок длины l, равномерно заряженный с линейной плотностью κ2, расположены в одной плоскости перпендикулярно друг другу. Расстояние между нитью и ближайшим к ней концом отрезка равно r0. Найдите силу, с которой нить действует на отрезок.
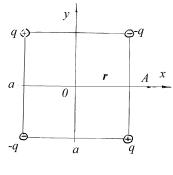
1.7. В вершинах правильного шестиугольника со стороной a помещаются точечные заряды одинаковой величины q . Найдите напряженность поля в центре шестиугольника при условии, что а) знак всех зарядов одинаков, б)
знаки соседних зарядов противоположны.
22 |
|
|
§1.Электрическое поле |
|||||
|
1.8. Электрический квадруполь состоит из |
|||||||
|
двух |
|
положительных |
|
и |
двух |
||
|
отрицательных одинаковых по величине |
|||||||
|
точечных |
зарядов |
q , |
расположенных в |
||||
|
вершинах |
квадрата |
со |
стороной |
a , как |
|||
|
показано |
на |
рис.1.11. |
|
Найдите |
|||
|
электрическое поле такого квадруполя в |
|||||||
|
точке |
А, |
находящейся |
на |
расстоянии |
|||
|
x >> a |
от его центра О, |
если линия ОА |
|||||
Рис.1.11 |
параллельна одной из сторон квадрата. |
|||||||
1.9. По круглой очень тонкой пластинке радиуса a равномерно распределен заряд Q . Найдите напряженность поля на оси, перпендикулярной к плоскости пластинки, как функцию расстояния z от ее центра. Исследуйте полученное выражение для z << a и z >> a .
1.10. Найдите напряженность поля, создаваемого плоским равномерно заряженным кольцом, на перпендикуляре к плоскости кольца, проходящем через его центр. Поверхностная плотность заряда равна σ , внутренний радиус кольца равен R1 , его внешний радиус - R2 .
1.11. На плоскости распределен положительный заряд с поверхностной плотностью σ . На другой, параллельной ей плоскости, отстоящей от первой на расстоянии d , распределен отрицательный заряд с вдвое большей плотностью. Нарисуйте картину силовых линий поля, создаваемого зарядами на плоскостях.
1.12. Полусфера радиуса R заряжена равномерно с поверхностной плотностью заряда σ. Найдите напряженность электрического поля в центре полусферы.
§1.Электрическое поле |
23 |
1.13. Внутри шара радиуса |
R , заряженного с постоянной объемной |
плотностью ρ , имеется сферическая полость радиусом r , в которой заряды отсутствуют. Центр полости смещен относительно центра шара на расстояние a ( a + r < R ). Найдите напряженность электрического поля внутри полости.
1.14. В модели атома Томсона предполагалось, что положительный заряд e
распределен внутри шара радиусом R = 10 −8 см . Как должна зависеть от радиуса плотность положительного заряда, чтобы электрон (точечная частица с отрицательным зарядом e ), помещенный внутри шара, совершал гармонические колебания? Найдите частоту колебаний электрона. Заряды механически друг на друга не действуют. Магнитным полем движущегося заряда пренебречь. Масса электрона m = 9,1 10 −31 кг .
|
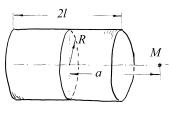
1.15. Цилиндр c радиусом основания R и |
|
высотой 2l заряжен по поверхности с |
|
постоянной поверхностной плотностью σ |
|
(см. рис.1.12). Считая, что основания |
|
цилиндра не несут заряда, определите |
|
напряженность электростатического поля |
Рис.1.12 |
в точке М на оси цилиндра на расстоянии |
|
aот его центра.
1.16.Бесконечная прямолинейная полоса шириной 2l заряжена с постоянной поверхностной плотностьюσ . Найдите напряженность электрического поля в точке, отстоящей от полосы на расстояние h . Точка находится на перпендикуляре, восстановленном из середины полосы.
24 |
§1.Электрическое поле |
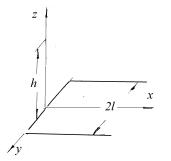
1.17. Полубесконечная полоса шириной
2l заряжена с постоянной поверхностной плотностью σ . Найдите напряженность электрического поля в точке М,
находящейся на расстоянии h от полосы на перпендикуляре, восстановленном в начале полосы из точки, лежащей на ее средней линии (см. рис.1.13).
1.18. Из четырех тонких заряженных палочек составлен квадрат со стороной l .
Две соседние стороны квадрата несут общий заряд +q , равномерно распределенный по их длине. Две другие стороны имеют общий заряд −q .
Определите напряженность электростатического поля в центре квадрата.
1.19. Две нити, совпадающие с положительными полуосями декартовой системы координат x0 y , равномерно заряжены с линейной плотностью κ.
Найдите напряженность электрического поля в точке M(a,a) a>0..
1.20. Три нити, совпадающие с положительными полуосями декартовой системы координат, равномерно заряжены с постоянной линейной плотностью κ . Найдите напряженность электрического поля в точке
M(a,a,a) a>0.
1.21. Две полубесконечные нити, равномерно заряженные с линейной плотностью κ , сложены так, что образуют прямой угол. Найдите величину напряженности электрического поля во всех точках прямой 0z , проходящей через вершину угла перпендикулярно плоскости, в которой лежат нити.
§2.Потенциал электрического поля |
25 |
§2. Потенциал электрического поля
Краткие теоретические сведения
Сила называется потенциальной, если ее работа вдоль любой замкнутой траектории равна нулю. Кулоновские силы удовлетворяют этому
|
r r |
r r |
|
|
r |
|
|
условию, поэтому |
∫Fdr |
= q′∫Edr |
= 0 , |
где |
F |
– сила, действующая |
на |
пробный заряд q′ |
|
|
|
|
|
|
r |
со стороны кулоновского поля с напряженностью |
E . |
||||||
Условие потенциальности электростатического поля можно записать в виде:
∫E dr = 0 . |
(2.1) |
Из этого равенства, на основании теоремы Стокса, следует
rot E = 0 . |
(2.2) |
Потенциалом ϕ электрического поля в точке М называют работу,
которую совершает поле при перемещении единичного заряда из этой точки в точку О, где договорились считать потенциал равным нулю:
O |
|
ϕ = ∫E dr . |
(2.3) |
M
В силу потенциальности электростатического поля, значение этого интеграла не зависит от выбора траектории интегрирования. Выбор точки О произволен и диктуется соображениями удобства. Обычно за нуль принимают потенциал бесконечно удаленной точки.
Как следует из (1.3) и (2.3), потенциал в точке М, удаленной на расстояние r от точечного заряда q , равен

26 |
|
|
|
§2.Потенциал электрического поля |
ϕ = |
q |
|
. |
(2.4) |
|
|
|||
4πε |
|
|||
|
0 r |
|
||
Для потенциальной силы можно ввести потенциальную энергию
W p = q ′ ϕ , где функция ϕ не зависит от величины пробного заряда.
Для потенциала, как и для напряженности, справедлив принцип
суперпозиции: потенциал поля, создаваемого несколькими зарядами, равен
сумме потенциалов, создаваемых каждым из них в предположении, что остальные отсутствуют.
Потенциал диполя на расстояниях, много больших его собственного размера, (потенциал точечного диполя) однозначно выражается через его
r
дипольный момент pe (см. Пример 2):
ϕ (M ) = |
(r pe ) |
|
4πε 0 r 3 , |
(2.5) |
r
где r – вектор, соединяющий центр диполя с точкой M.
Если в некотором объеме V распределен заряд с объемной
плотностью ρ (r ), |
то потенциал, создаваемый этим зарядом в произвольной |
||||||
точке пространства М, определяется как |
|
||||||
ϕ (M ) = |
|
1 |
|
∫ |
ρdV |
. |
(2.6) |
4πε |
|
|
|||||
|
0 |
r |
|
||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
Напряженность электростатического поля однозначно связана с его
потенциалом. При этом соотношение, обратное (2.3), имеет вид:
E = − gradϕ . |
|
(2.7) |
|||
Применяя эту формулу к (2.5) можно найти напряженность поля |
|||||
точечного диполя: |
|
|
|||
E = |
1 |
|
3(pe n)n − pe |
, |
(2.8) |
|
|
||||
4πε 0 |
|
r 3 |
|
|
|
r |
|
|
|
|
r |
где n – единичный вектор, направленный вдоль |
r . |
||||
§2.Потенциал электрического поля |
27 |
|
Эквипотенциальными |
поверхностями называют |
поверхности |
равного потенциала. Так как |
компонента вектора gradϕ , |
касательная к |
эквипотенциальной поверхности, всегда равна нулю, силовые линии поля в каждой точке направлены по нормали к соответствующей эвипотенциальной поверхности (см. Рис 2.4).
Пример 2.1. Найдите работу, совершаемую силами однородного поля напряженности E над зарядом q при его перемещении из точки 1 с радиус-
вектором r1 |
в точку 2 с радиус-вектором r2 |
по произвольной траектории. |
||||||||||||||||||||||||
Решение. По определению работы |
|
|
dA = F dr . |
Для однородного поля |
||||||||||||||||||||||
F = q E , откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
r 2 |
|
r |
|
r |
|
r |
|
|
v |
|
|
|
|
|||
A12 = q∫E dr = qE ∫dr = qE(r2 |
− r1 ) . |
|
(2.9) |
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
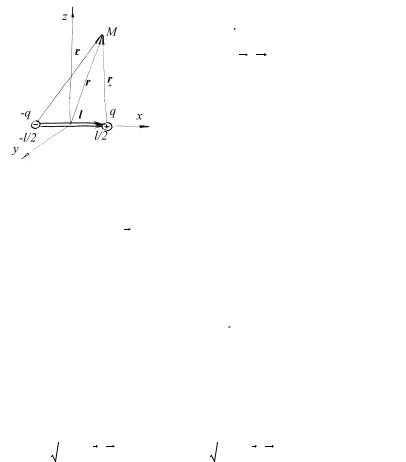
Пример 2.2. Найдите потенциал и |
|
|
|
|
||||||||||||||||||||||
напряженность |
|
|
электрического |
|
|
поля, |
|
|
|
|
||||||||||||||||
создаваемого |
|
|
|
точечным |
|
диполем |
|
|
с |
|
|
|
|
|||||||||||||
дипольным моментом p e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. Направим ось 0x |
|
из середины |
|
|
|
|
||||||||||||||||||||
отрезка, соединяющего заряды диполя, от |
|
|
|
|
||||||||||||||||||||||
отрицательного заряда к положительному. |
|
|
|
|
||||||||||||||||||||||
Положение точки М пространства будем |
|
|
|
|
||||||||||||||||||||||
описывать |
|
|
|
|
|
радиус-вектором |
|
|
|
|
|
|
r . |
|
|
|
|
|||||||||
Использовав обозначения, приведенные на |
|
|
Рис.2.1 |
|||||||||||||||||||||||
рис.2.1, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
( |
) |
|
|
|
q |
|
1 |
1 |
|
|
|
q |
|
|
|
|
r − r |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
+ |
|
|
|
||||
ϕ |
= |
|
4πε |
|
|
− r |
4πε |
|
|
|
|
|
|
|
||||||||||||
|
M |
|
|
0 |
r |
|
= |
0 |
|
|
|
r r |
, |
(2.10) |
||||||||||||
|
|
|
|
|
|
|
|
+ |
|
− |
|
|
|
|
|
|
+ |
− |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
где r = |
|
r 2 |
− 2(r l / 2)+ l 2 / 4 |
|
и |
r |
|
= |
|
|
|
r 2 + 2(r l / 2)+ l 2 / 4 |
||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|

28 |
|
|
|
|
|
|
|
|
|
|
|
|
§2.Потенциал электрического поля |
||||
При r >> l |
выражение |
(2.10) |
упрощается, |
так как |
r+ ≈ r − (r l )/(2r ) |
и |
|||||||||||
r− ≈ r + (r l )/(2r ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ (M ) = |
|
q(r l ) |
|
= |
(r p e ) |
|
|
|
|
|
|
(2.11) |
|
||||
|
4πε 0 r 3 |
4πε 0 r 3 |
|
|
|
|
|
|
|
||||||||
Здесь p e = q l |
дипольный момент диполя. |
|
|
|
|
||||||||||||
Напряженность поля по известному потенциалу найдем согласно |
|||||||||||||||||
(2.7). Применяя к (2.11) формулы векторного анализа |
(см. Приложение |
) |
|||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = |
3 pe x |
n − |
|
p e |
= |
1 |
|
|
3(p e n)n − pe |
. |
(2.12) |
|
|||||
|
|
|
|
|
|
4πε |
|
|
|
||||||||
|
4πε 0 r 4 |
|
|
4πε 0 r 3 |
|
0 |
|
|
r 3 |
|
|
||||||
Пример 2.3. Определите силу, действующую на точечный диполь с дипольным моментом p e в неоднородном электрическом поле E(r ).
Решение. Рассмотрим диполь малого, но конечного размера (см. рис.2.1).
Проекция силы, действующей |
|
|
на |
диполь, |
на |
ось |
0x |
|
равна |
|||||||||||||
Fx |
= q[E x (l / 2,0,0)− E x (− l / 2,0,0)]. |
|
Раскладывая |
|
в |
|
ряд |
|
Тейлора |
|||||||||||||
напряженность поля в окрестности начала координат, получим |
|
|
|
|||||||||||||||||||
F |
|
= q |
∂E x |
l = q(l )E |
|
= (p |
|
)E |
|
, |
|
где |
= i |
∂ |
+ j |
∂ |
+ k |
∂ |
. |
|||
|
x |
|
∂x |
x |
|
e |
|
x |
|
|
|
|
|
∂x |
|
∂y |
|
∂z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналогично выводятся соотношения для Fy |
= (pe )E y |
и |
Fz |
= (pe )E z . |
||||||||||||||||||
Полученные скалярные равенства можно объединить в одно векторное |
||||||||||||||||||||||
|
|
|
F = (p e )E . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.13) |
|||
Пример 2.4. Найдите энергию взаимодействия W |
|
двух |
диполей, |
|||||||||||||||||||
находящихся на расстоянии |
r >> li |
( l i − |
размер |
i − го |
диполя) |
друг от |
||||||||||||||||
друга. Дипольные моменты диполей p1 |
и p2 . |
|
|
|
|
|
|
|
|
|
||||||||||||
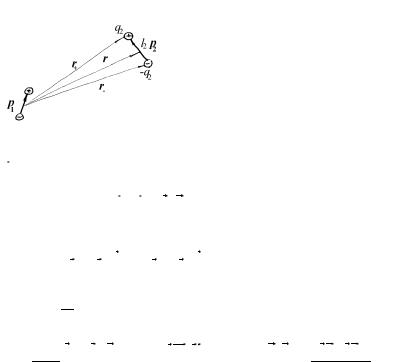
§2.Потенциал электрического поля |
29 |
Решение. Энергия взаимодействия двух диполей - это дополнительная энергия,
которая появляется у диполя в поле,
создаваемом другим диполем. Для диполя
p 2 она равна (рис.2.2)
W2 = q2 (ϕ A − ϕ B ) ,
где потенциал ϕ, |
|
|
|
|
|
|
|
|
|
|
|
Рис.2.2 |
||||
создаваемый диполем |
||||||||||||||||
p1 , задается выражением (2.11). Подставляя его в W2 , получаем |
||||||||||||||||
|
|
|
q |
|
|
(r + |
p ) |
|
(r − p |
|
|
|
||||
|
= |
|
2 |
|
− |
1 |
) |
|||||||||
W2 |
|
|
|
|
|
1 |
|
|
|
. |
||||||
4πε 0 |
|
|
3 |
|
r 3 |
|
|
|||||||||
|
|
|
|
r |
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ |
|
|
− |
|
|
|
||||
Учтем, что |
r + |
= r + |
l 2 |
и |
r − = r − |
l 2 |
, и разложим W2 в ряд по малому |
|||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||
параметру
W2 = q2
4πε 0
l 2 . Отбрасывая в разложении члены порядка r
(r + − r − )p |
1 |
|
3q |
2 |
|
(r p )(rl 2 ) |
|
1 |
p |
1 |
p |
2 |
|
||
|
− |
|
1 |
|
= |
|
|
|
|
− |
|||||
|
|
4πε 0 |
|
|
|
4πε 0 |
|
|
|
|
|||||
r 3 |
|
|
|
r 5 |
|
r 3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
2 |
3 |
|
|
|
|
|
|
|
, получаем |
|||
|
|
|||||
r |
|
|
|
|
||
3(r p1 )(r p 2 ) |
(2.14) |
|||||
|
|
|
r |
5 |
|
|
|
|
|
|
|
|
|
Пример 2.5. В условии примера 4 из первого параграфа определите потенциал в произвольной точке М на перпендикуляре к плоскости кольца,
восстановленном из его центра. Используя найденное выражение для потенциала, найдите напряженность электрического поля в точке М.
Решение. Так же как и в примере 4 из первого параграфа введем
координаты точки M (0,0, z ) и точечный заряд на кольце |
(точка N на |
кольце характеризуется углом ψ , отсчитываемым от оси |
0 x , которому |
даем приращение dψ ) (см. рис.1.8). Потенциал заряда dq в точке М равен

30 |
|
|
|
|
|
|
|
|
|
|
§2.Потенциал электрического поля |
||
dϕ = |
|
|
dq |
|
|
= |
(Q 2π )dψ |
||||||
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
4πε |
0 |
|
a 2 |
+ z 2 |
|
|
4πε |
0 |
a 2 |
+ z 2 |
||
Интегрируя по ψ от 0 |
до 2π , окончательно получаем |
||||||||||||
Q
ϕ =  . (2.15)
. (2.15)
4πε 0  a 2 + z 2
a 2 + z 2
Используя (2.7), находим напряженность на оси кольца
E |
|
= − |
∂ϕ |
= |
Q |
|
|
|
z |
|
, |
|
z |
∂z |
4πε 0 |
( |
2 |
+ z |
2 )3 / 2 |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
a |
|
|
|||
что совпадает с выражением (1.10), полученным ранее в параграфе 1.
Пример 2.6. Диск радиусом a заряжен с поверхностной плотностью σ .
Найдите потенциал в произвольной точке на оси диска, перпендикулярной к его плоскости.
Решение. Разобьем диск на кольца радиусом ρ и толщиной dρ . На таком кольце находится заряд dq = σ 2πρ dρ . Потенциал на оси такого кольца найден ранее в примере 5 данного параграфа и задается выражением (2.15)
dϕ (z ) = |
|
|
dq |
|
|
|
|
|
= |
|
|
|
σ |
|
|
|
|
ρ dρ . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
4πε |
0 |
|
ρ 2 |
+ z |
2 2ε |
0 |
ρ 2 |
+ z 2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интегрируя это выражение по ρ от 0 до a получим |
|
|
|
|||||||||||||||||||||||||
a |
|
σ |
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕ (z ) = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ρ dρ = |
|
|
|
|
|
a |
|
+ z |
|
− z . |
|
(2.16) |
||||||||
|
|
|
|
|
|
|
|
|
2ε |
|
|
|
|
|||||||||||||||
0 2ε 0 ρ |
2 |
+ z |
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При z → ∞ выражение (2.16) принимает вид ϕ (z ) → |
σa 2 |
= |
Q |
, то есть |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ε 0 z |
|
4πε 0 z |
|
совпадает с полем точечного заряда Q = πσa 2 .
