4.2.3 Влияние взаимодействия междуRyR-каналами на стабильность осцилляций системы

Далее в ходе моделирования динамики Са²⁺-«часов» варьировался параметр взаимодействия между каналами в диапазоне от 0 до 2.5, и исследовалось влияние этого параметра на устойчивость осцилляций Са²⁺-«часов».

Результаты наблюдений авторитмических осцилляций изолированных внутренних Са²⁺-«часов» в виртуальном эксперименте представлены на рисунке 4.15.

Как показано на рисунке, при увеличении параметра без учета взаимодействия нарушается постоянство амплитуды зависимости. Эти нарушения проявляются в частотных и амплитудных флуктуациях и внеочередных высвобождениях, нарушающих гармонический или релаксационный режим колебаний. Под внеочередными высвобождениями (обозначены на графиках красными стрелками) подразумеваются высвобождения при достаточно малой концентрациии, соответственно, при отрицательном значении параметра эффективного давленияp, как видно из временных зависимостей p(t) на вставках к графикам (рис.4.15).

Данные внеочередные высвобождения возникают вследствие электронной активации RyR-каналов и объясняются тем, что при достаточно большой скорости заполнения СР увеличивается частота высвобождений и не успевает диффундировать в цитозоль из диадного пространства. В связи с этим вероятность электронных переходов не успевает уменьшиться до нуля, инициируя спонтанные высвобождения. Однако, как видно из рисунка, наблюдается следующая закономерность: при увеличении параметра конформационного взаимодействия соседних RyR-каналов уменьшается уровень шумов и также количество внеочередных всплесковCa_SS пример, при =10 с^-1 на первой секунде происходит восемь внеочередных высвобождений при k=0, в то время как при k=1 их число снизилось до двух. Следовательно, усиление кооперативности привносит стабильность осцилляций Са²⁺-«часов».

Как было установлено экспериментально [126, 127], кооперативность RyR-каналов обеспечивает группа специфических белков FKBP 12.6, расположенных между каналами и стабилизирующих их динамику. При ослаблении действия данного белка с помощью различных препаратов было обнаружено нарушение самосогласованной динамики всего кластера [128], увеличение продолжительности локальных высвобождений Са²⁺ в диадное пространство (длительность спарков) и нарушения ритма сокращений [129, 130].

Изучение этих нарушений играет огромную роль в исследованиях возникновения аритмии. Внеочередные колебания внутренних Са²⁺-«часов», также как и флуктуации могут являться причиной нарушения автоволновой активности клеток водителя сердечного ритма в целом, что может стать аритмогенным фактором для всего миокарда.

Таким образом, на основе интеграции ЭК-модели RyR-каналов в модель кальциевой динамики можно сделать вывод, что введенная в рассмотрение кооперативная динамика RyR-каналов является стабилизирующим фактором, предотвращающим нежелательные сбои в активности клеток водителей сердечного ритма.

4.2.3 Эффект случайной остановки автоколебаний

На следующем этапе моделирования динамики Са²⁺-«часов» в настоящей работе исследовалось влияние скорости высвобождения Са²⁺ через одиночный RyR-канал на характер осцилляций системы.

Временные зависимости относительного числа открытых каналов и концентрации высвободившегося кальция () при различных значениях(от 1 до 100 с^-1) без учета и с учетом взаимодействия между RyR-каналами показаны на рисунке 4.16.

Эти зависимости показывают, что без учета взаимодействия при достаточно больших (>50 с^-1) наблюдаются устойчивые релаксационные колебания Са²⁺-«часов», в то время как в интервале от 10 до 50 с^-1 проявляются как гармонические колебания, так и спонтанные переходы к высокочастотным стохастическим осцилляциям с малой амплитудой вблизи определенного среднего значения (~0.2 мкМ). Дальнейшее уменьшение параметра(5 с^-1) приводит к переходу осциллятора в квазиравновесное состояние.

При учете взаимодействия между каналами наблюдается стабилизация осцилляций концентрации Са²⁺ в диадном пространстве при >15 с^-1 (рис. 4.16б). Дальнейшее уменьшение параметра приводит кспонтанным переходам осциллятора в стационарное состояние, то есть к постоянному току Са²⁺ из СР.

Таким образом, в численных экспериментах, проведенных в данной работе, впервые наблюдался принципиально новый эффект случайной остановки Са²⁺-осциллятора. Детальный анализ этого явления показал, что он заключается в появлении в процессе высвобождения/заполнения устойчивого кластера открытых каналов (2х2, 3х2 и проч.), через который и осуществляется стационарное высвобождение ионов Са²⁺ в диадное пространство. На рисунке 4.17 приведен пример данного перехода в состояние стационарного высвобождения на графиках зависимостей и, и изображен вид решетки RyR-каналов при переходе в данное состояние (светлыми квадратами обозначены открытые, темными – закрытые каналы).

Анализ этого рисунка позволяет сделать вывод, что формирование устойчивого кластера 3х2 RyR-каналов не является мгновенным, а происходит следующим образом: каналы, неокруженные открытыми соседями, при понижении Ca_jSR в процессе высвобождения туннелируют в закрытое состояние. Вероятность туннелирования отрытых каналов с открытыми соседями достаточно мала, что приводит к появлению стабильного кластера в системе, стабильность которого обеспечивает конформационное взаимодействие между RyR-каналами.

Возвращаясь к рисунку 4.16, можно заключить, что необходимыми условиями для проявления обнаруженного эффекта являются достаточно сильное взаимодействие между соседними каналами и высокий уровень критического значенияпо сравнению со средним значением. В этом случае концентрация Са²⁺ в диадном пространстве не достигает критического значения, в связи с этим не происходят электронные переходы, которые способны нарушить стационарность системы.

Для объяснения причин устойчивости открытого состояния каналов в кластере на рисунке 4.18 изображены конформационные потенциалы группы шести открытых каналов и соседних закрытых. Взаимодействие между открытыми каналами приводит к перенормировке конформационного потенциала в сторону стабильности открытого состояния. В связи с этим, канал, окруженный открытыми соседями, не может быть инактивирован даже при отрицательном значении параметра эффективного давления р, так как процесс туннелирования возможен только в случае глобального минимума обратного состояния.

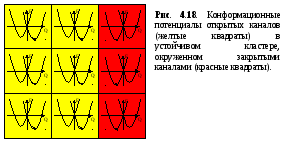
В связи с тем, что случайные остановки Са²⁺-«часов» ранее не наблюдались, возникла необходимость более детального исследования данного эффекта, а также изучение влияния динамических параметров на размеры и устойчивость кластеров открытых каналов.