3.7 Динамика одиночного RyR-канала при установившемся уровне cis[Ca]

На следующем этапе данной работы исследовалось поведение изолированных RyR-каналов при установившемся уровне cis[Ca] после выхода в динамическое равновесие (участок III на рисунке 3.23а).

Динамическое равновесие определяется постоянным значением средней вероятности пребывания RyR-канала в открытом состоянии на больших интервалах времени. Как показывают результаты экспериментов по изучению кинетических свойств RyR-канала при стационарных условиях, средняя вероятность пребывания канала в открытом состоянии напрямую зависит от уровня cis[Ca] [13, 17, 20].

В связи с этим в настоящей работе необходимо было исследовать активность одиночного RyR-канала при стационарных условиях и установить способность электронно-конформационной теории объяснить эффекты динамики RyR-канала при постоянном уровне cis[Ca], ранее выявленные экспериментально.

3.7.1 Зависимость активности RyR-канала от времени

В начале эксперимента по исследованию активности RyR-каналов все каналы в ансамбле были закрыты, а в момент времени t=0 при cis[Ca]>0 происходил быстрый процесс активации и дальнейшей процесс медленной адаптации каналов. Регистрация активности канала в численных экспериментах проводилась, после выхода на стационарный режим, начиная с момента t=3 c.

На рисунке 3.26 представлены результаты численных экспериментов по наблюдению активности RyR-канала при стационарных условиях. Данный эксперимент проводился при следующих значениях интенсивностей переходов: мс^-1, мс^-1, мс^-1, мс^-1, мс^-1. Эти значения соответствуют значению cis[Ca]=0.5 мкМ согласно формуле (2.6). Активность канала исследовалась на малых интервалах длительностью 10 мс, что позволило построить график зависимости вероятности пребывания RyR-канала в открытом состоянии от времени (рис. 3.27б).

Как видно из графика, зависимость вероятности пребывания канала в открытом состоянии является неоднородной, и динамика RyR-канала при стационарных условиях носит стохастический характер.

Гистограмма распределения вероятности пребывания канала в открытом состоянии (рис. 3.28) имеет два локальных максимума в точках, соответствующих и. Локальный минимум соответствует значениюи определяет граничное значение вероятности пребывания канала в открытом состоянии[121], которое разделяет так называемыемоды активности RyR-канала на текущем интервале. При значении интервал характеризуется высокой активностью (мода Н), приканал находится в моде низкой активностиL. Значение вероятности определяет нулевую активность канала (модаI). Зависимость положения канала в модах H, L и I в зависимости от времени изображена на рисунке 3.27в. Информация о положении канала в той или иной моде позволяет более детально описать его активность в текущий момент времени.

3.7.2 Зависимость активности RyR-канала от уровня cis[Ca]

На рисунке 3.29 изображены зависимости активности RyR-канала от времени при различных значениях cis[Ca] (открытое состояние соответствует значению 1).

Для сравнения результатов численных реализаций с экспериментальными данными, на рисунке 3.30 представлены графики экспериментальные регистрации активности RyR-канала при различных значениях cis[Ca] [15].

Сравнивая рисунок 3.30а с результатами моделирования (рис. 3.30б), можно сделать вывод, что результаты численных экспериментов находятся в хорошем согласии с экспериментальными данными.

В работе при проведении анализа кинетических характеристик динамики RyR-канала в рамках модели, были построены графики зависимости от концентрации Са²⁺ в cis-части при различных значениях числа кластеров в активных центрах канала, представленные на рисунке 3.31.

Зависимость активности RyR-канала при стационарных условиях от концентрации цитозольного Са²⁺ носит колоколообразный характер: растет с увеличением cis[Ca] в интервале от 0 до 100 мкМ и спадает при cis[Ca]>100 мкМ.

Эффект понижения при достаточно больших значениях cis[Ca] получил в литературе название Са²⁺-зависимой инактивации [24] и является одним из ключевых феноменов тонкой регуляции RyR-канала ионами Са²⁺. Однако следует отметить, что концентрации cis[Ca]>100 мкМ не являются физиологическими и представляют интерес только для экспериментов in vitro.

Приведенные на рисунке 3.31б графики зависимости вероятности пребывания в инактивационном состоянии () от cis[Ca] говорят о том, что с ростом cis[Ca] увеличивается частота электронных переходов в инактивационное состояние, в связи с этим повышается.

При исследовании динамических рядов активности RyR-канала при различных значениях cis[Ca] были изучены моды активности канала и построена гистограмма распределения по пребываниям в той или иной моде, представленная на рисунке 3.32.

Были введены следующие моды активности:

• Мода С/I соответствует пребыванию канала в закрытом состоянии С или в инактивационном состоянии I. На гистограмме состояния С и I разделены в третьем столбце. Вероятность пребывания в открытом состоянии в этой моде является нулевой.

• Моде H соответствуют длительные пребывания в открытом состоянии О и частые переходы из закрытого состояния в открытое (при этом время пребывания в открытом состоянии больше, чем в закрытом: 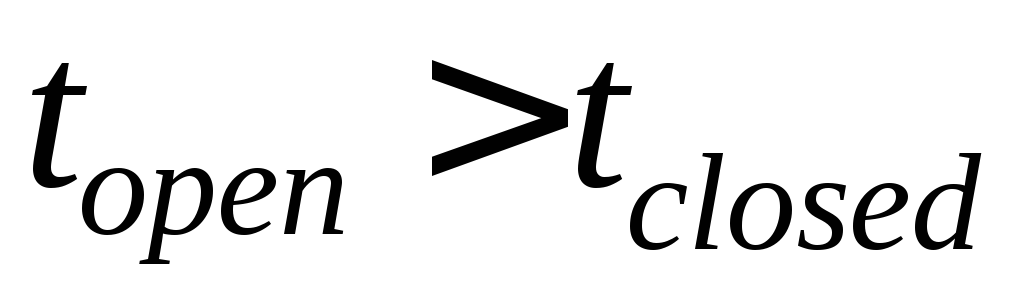). В данной моде.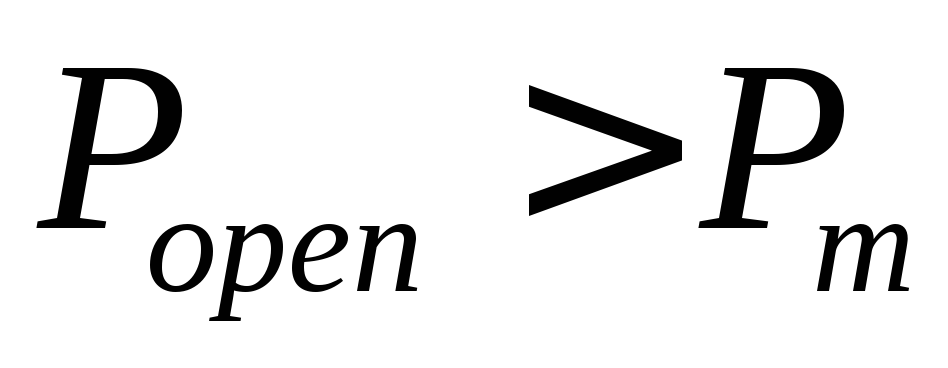

• Моде L соответствует серия кратковременных пребываний в открытом состоянии (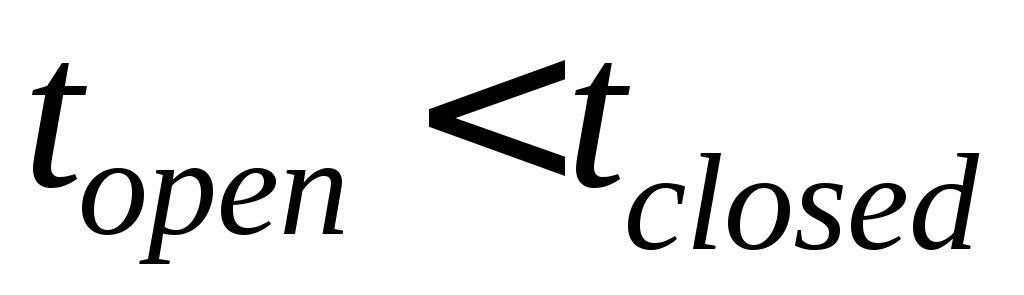). Закрытия происходят вследствие переходов в конформационно закрытое состояние и в инактивацинное состояние. В моде низкой активности:.

Как ясно из рисунков 3.31 и 3.32, с ростом cis[Ca] наблюдается увеличение вероятности нахождения системы в инактивационном состоянии, и оно становится превалирующим после значения cis[Ca]=100 мкМ, которое соответствует максимуму зависимости .

Согласно экспериментальным данным [20], активность RyR-каналов в кардиомиоцитах становится нулевой при очень высоких значениях концентрации цитозольного Са²⁺ (5-10 мМ), которые, предположительно, недостижимы в клетках. Однако, Са²⁺-зависимая инактивация также как и адаптация, является механизмом негативного контроля, обеспечивающим своевременное завершение процесса высвобождения Са²⁺ из СР во время клеточного цикла.

3.7.3 Влияние ионов Mg2+ на динамику одиночного RyR-канала

Ионы Mg²⁺ как и ионы Са²⁺ обладают сильным сродством с активационной частью RyR-канала, однако, занимая вакантные места на активационных частях, они не приводят к открытию канала [122, 123].

Как и в случае взаимодействия ионов Са²⁺с активными центрами, в настоящей диссертационной работе предлагается статистический подход к рассмотрению конкурентного присоединения ионов Mg²⁺ и Са²⁺ к активным центрам канала.

На рисунке 3.33а схематично представлен процесс присоединения ионов Са²⁺ и Mg²⁺ с активному центру канала. Заполнение ионами активных мест связывания активного центра описано с помощью диаграммы Эйлера (рис. 2.31б).

Было сделано предположение, что если в кластер активного центра попадают оба типа ионов, то вероятность присоединения того или иного типа ионов к свободному центру равняется ½.

Пусть – относительная концентрация ионов Mg²⁺ вблизи канала, где – максимальная концентрация магния, при которой заполнены все места связывания активного центра канала; – относительная концентрация ионов Са²⁺.

Далее определялась вероятность нахождения более чем k ионов Са²⁺ в активном центре канала с учётом присутствия на нем ионов Mg²⁺.

Относительное число активных мест, в которых находятся только ионы Са²⁺ в кластере: ; относительное число секторов, в которых находятся ионы Са иMg, но присоединяются ионы Са: . Соответственно, относительное число «сработавших» ионов Са²⁺ равно . Число комбинацийk ионов Са²⁺ в z частях кластера равно . Наконец, вероятность обнаружения более чемk ионов Са²⁺ в кластере активной части равняется:

. (3.21)

В численных экспериментах значение cis[Ca] варьировалось в диапазоне от 0.05 до 1000 мкМ. В первой части экспериментов не учитывалось влияние ионов Mg²⁺, и интенсивность электронных переходов в зависимости от cis[Ca] рассчитывалась по формуле 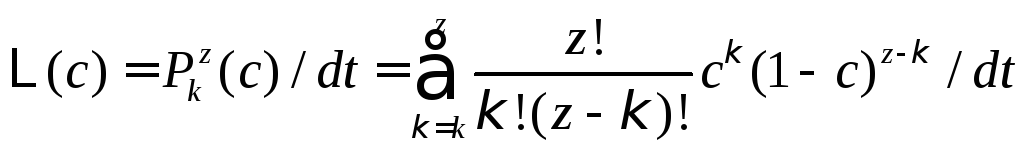(см. формулу 2.10), гдес – относительная концентрация ионов Са²⁺ в cis-части.

Во второй серии экспериментов учитывалось присутствие Mg²⁺ в растворе (Mg=3 мМ), и ирассчитывались согласно формуле (3.21). Графики зависимостей интенсивностей электронных переходов с учетом и без учетаMg²⁺ представлены на рисунке 3.33.

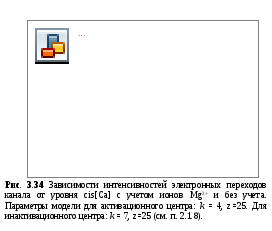
Как видно из рисунка, учет Mg²⁺ сдвигает зависимость вниз, то есть статистический подход хорошо описывает ингибирующие свойства ионовMg²⁺.

На рисунке 3.35 представлены графики зависимости вероятности пребывания канала в открытом состоянии от концентрации Са²⁺ в cis-части в отсутствии и в присутствии ионов Mg²⁺ .

Как видно из графика, зависимости имеют колоколообразную форму с максимумом, соответствующим значению cis[Ca]=50 мкМ (без учетаMg²⁺) и cis[Ca]=100 мкМ (с учетом Mg²⁺). Другими словами, при учете ионов Mg²⁺ происходит сдвиг вправо зависимости . Для сравнения на рисунке 3.35б приведен график из работы [20]. Анализ представленных кривых говорит о том, что результаты моделирования с высокой степенью точности совпадают с экспериментальными данными.

В присутствии ионов Mg²⁺ в растворе, в котором находится RyR-канал, график зависимости сдвигается вниз и вправо, то есть максимум достигается при больших значенияхи максимум функции меньше, чем в отсутствие ионовMg²⁺, конкурирующих с активными ионами Са²⁺.

Ионы Mg²⁺ являются потенциальными ингибиторами RyR-каналов, в связи с этим находят активное применение в фармакологии и терапии для понижения частоты высвобождений Са²⁺ для предотвращения аритмии и других патологий.

Модификация электронно-конформационной модели и введение инактивационного состояния позволили описать не только основные свойства изолированных RyR-каналов, но и важнейшие тонкие эффекты взаимодействия каналов с ионами Са²⁺, которые являются механизмами негативного контроля и должны учитываться при моделировании процесса КВВК.