3.2 Медленная конформационная динамика RyR-канала

На первоначальном этапе с целью изучения активности одиночного RyR-канала исследовалось влияние основных констант конформационного потенциала (2.4) и коэффициентов, входящих в уравнение Ланжевена (2.7) на характер динамики канала.

3.2.1 Параметр эффективного трения г. Конформационная динамика RyR-канала

Коэффициент эффективного трения Г, входящий в уравнение Ланжевена (2.7), влияет на характер изменения конформационной координаты Q со временем. Приведенное уравнение (М=1) изменения конформационной координаты при отсутствии тепловых возмущений () может быть записано в терминах затухающего гармонического осциллятора:

, (3.4)

где – характерная частота колебаний гармонического осциллятора.

При малом трении (Г<2) общее решение может быть представлено в виде [118]:

, (3.5)

где – частота свободных колебаний;А, φ – амплитуда и фаза затухающих колебаний, соответственно.

При Г=2 затухание называется критическим. Начиная с этого значения коэффициента трения, система совершает так называемое неколебательное движение. В этом случае движение происходит по закону:

, (3.6)

где А и В – константы.

Критическое затухание примечательно тем, что именно в этом случае осциллятор быстрее всего стремится к положению равновесия, причем, если коэффициент трения Г меньше критического, то он дойдет до положения равновесия быстрее, однако, при этом «проскочит» его по инерции. В этом случае осциллятор будет совершать колебания вблизи точки минимума.

При значениях Г больше критического (Г>2) решение выглядит следующим образом:

, (3.7)

где . В этом случае осциллятор будет экспоненциально стремиться к положению равновесия, причем тем медленнее, чем больше трение.

Поскольку в электронно-конформационной модели , то критическое значение трения определяется как:

. (3.8)

Величина коэффициента Г варьировалась выше и ниже критического значения . При фиксированном значении параметраК=12 значение Г_crit≈6.8. При Г< Г_crit наблюдались колебания системы вблизи минимума потенциала (рис. 3.4а, колебания отмечены пунктирным прямоугольником). При Г> Г_crit наблюдался неколебательный случай динамики RyR-канала (рис. 3.4б)

При проведении дальнейших численных экспериментов параметр Г выбирался по значению больше критического (Г=7).

3.2.2 Влияние коэффициента упругости каналаK на форму конформационного потенциала

Конформационный потенциал (2.4) имеет два локальных минимума со следующими конформационными координатами:

. (3.9)

Первый минимум соответствует закрытому, второй - открытому состоянию канала. Положение этих минимумов зависит от величины коэффициента упругости К.

Варьируя значения К в широком интервале [1; 20] при фиксированном наборе остальных коэффициентов в (2.4), можно исследовать влияние этого параметра на свойства конформационного потенциала. Типичные графики конформационного потенциала представлены на рисунке 3.5.

Как видно из рисунков 3.5 и 3.6, с увеличением значения коэффициента K уменьшается расстояние между минимумами КП и крутизна ветвей КП. При изучении конформационной динамики канала исследовалось среднее время релаксации канала из точки, соответствующей одному минимуму КП в другой минимум ().

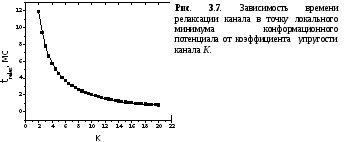
Как показывает график, представленный на рисунке 3.7, с ростом К уменьшается значение . Другими словами, варьируя параметрК, можно менять скорости конформационной релаксации канала в ЭК-модели. В дальнейших экспериментах значение К выбиралось равным 12.