2.3 Методы численной реализации модели

Электронно-конформационное состояние RyR-канала описывается стохастическим дифференциальным уравнением (2.7) со случайным изменением правой части и с переключением вследствие электронных и туннельных переходов (2.8, 2.10).

В формулах (2.4, 2.5) переменная электронного состояния является дискретной и принимает два значения: 0 (электронно закрытое) и 1 (электронно отрытое состояние). Слагаемоев уравнении (2.7) отвечает за аддитивные шумы в виде случайного винеровского процесса. Таким образом, компьютерная реализация ЭК модели должна быть основана на численных методах интегрирования стохастических дифференциальных уравнений и методах реализации марковских процессов. Сочетание этих методов позволило построить две численные схемы для получения наборов реализаций.

2.3.1 Метод Эйлера-Марайамы

Наиболее известным методом решения дифференциальных уравнений со случайными членами является явный метод Эйлера, обобщенный для стохастических уравнений Марайамой (Maruyama) в 1955 году, поэтому этот метод иногда называют методом Эйлера-Марайамы [114, 115].

Стохастическое дифференциальное уравнение Ито, описывающее изменение со временем некоторой переменной , имеет вид [115]:

, (2.29)

Пусть оно задано на интервале времени [0; T] с начальными условиями , гдеи– измеримые функции, аотвечает за винеровский процесс. Данный интервал времени можно дискретизировать с шагом, гдеL – число шагов на выбранном интервале. Дискретный набор моментов времени на интервале обозначается как: ,– приближенное решение уравнения (2.29) на каждомi-ом шаге.

Согласно схеме Эйлера-Марайамы решение на последующем шаге находится как:

, (2.30)

где – приращение винеровского процесса, для которого справедливо соотношение [115]:

,

где – нормально распределенная случайная величина с нулевым средним и единичной дисперсией. С учетом этого схема метода принимает вид:

где - нормально распределенная случайная величина (N(0,1)), вычисленная методом Монте Карло на i-ом шаге интегрирования системы уравнений.

Если обозначить скорость изменения координаты Q как , то для уравнения Ланжевена (2.7) в ЭК-модели, описывающего изменение конформационной координаты RyR-канала, метод Эйлера-Марайамы имеет вид:

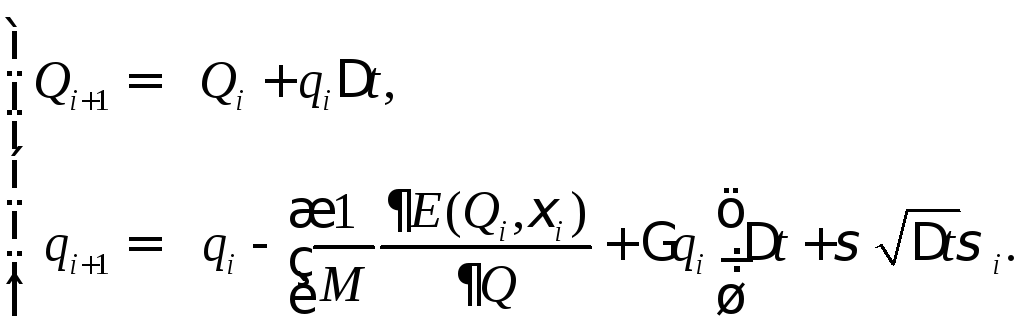(3.31)

2.3.2 Реализация электронных и туннельных переходов. Метод Монте-Карло

Электронные и туннельные переходы в ЭК-модели можно представить в терминах дискретного марковского процесса с различными вероятностями переходов между состояниями марковской цепи. Для описания случайных марковских процессов обычно используют метод Монте-Карло, который заключается в применении генератора псевдослучайных чисел для моделирования случайного процесса переходов между состояниями.

Простейшим способом описания инактивационного состояния является введение новой переменной μ, принимающей два значения: μ=1, если канал инактивирован, μ=0 в остальных случаях. Если ввести функцию Хэвисайда 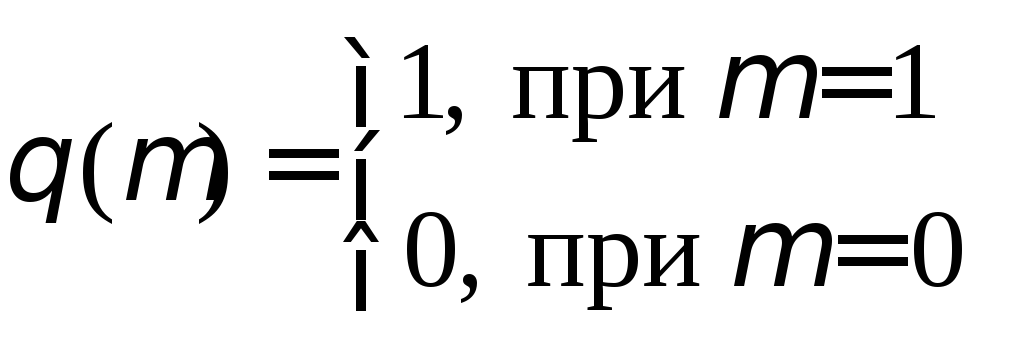, то с учетом новой переменной адиабатический конформационный потенциал (2.4) имеет следующей вид:

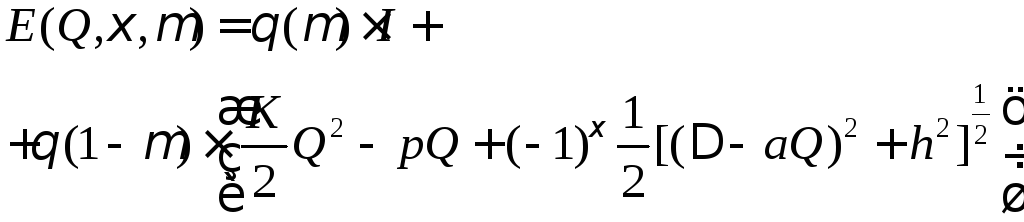, (2.32)

где – энергия инактивационного состояния.

Диабатический конформационный потенциал (2.5) может быть описан следующей формулой:

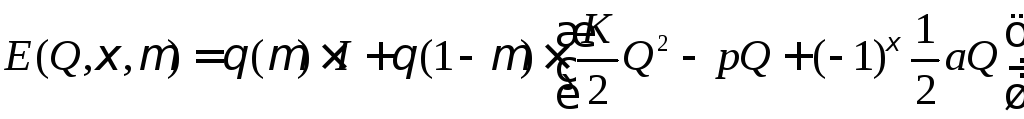. (2.33)

Для инактивационного состояния, была введена новая переменная μ.

Рассмотрим состояние канала 1: в определенный момент времени . В следующий момент временисистема может оказаться в состояниях 2: или 3: или 4: (рис. 2.15).

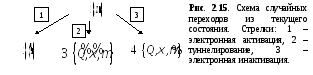
Предполагается, что потоки событий электронных и туннельных переходов между состояниями являются пуассоновскими. Опираясь на это предположение, дискретизируем марковский процесс с таким малым шагом по времени , что за этот промежуток времени может произойти только одно событие перехода.

На каждом шаге интегрирования случайного процесса вероятности туннельного, электронного перехода между ветвями КП и вероятность перехода в инактивационное состояние определялись следующим образом:

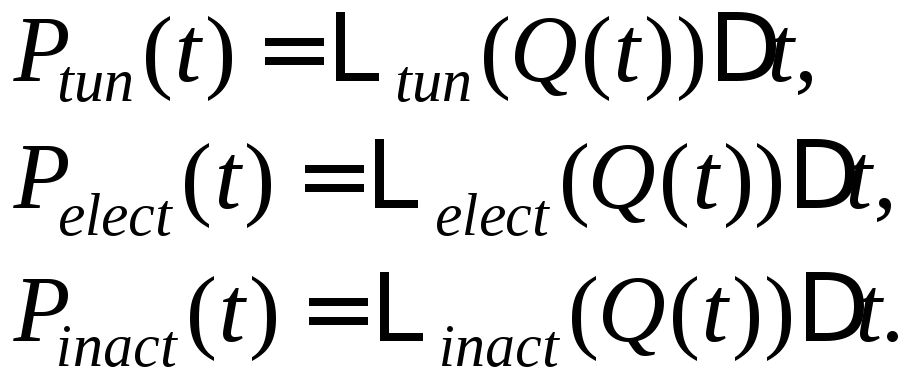(3.34)

Так как события туннельных и электронных переходов являются независимыми, то вероятность покинуть состояние 1 за время равна.

Однако для построения цепи нужно знать еще вероятности переходов в «состояние 2» и «состояние 3» при условии, что канал покинет «состояние 1». Эти вероятности могут быть вычислены по следующим формулам:

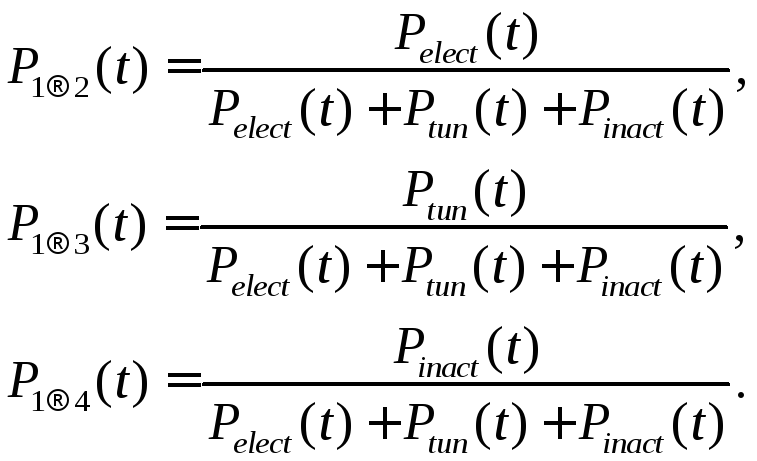(2.35)

В данной работе предполагается, что при осуществлении быстрых переходов не происходит изменения конформационной координаты по уравнению Ланжевена. Медленная конформационная динамика в течение промежутка времени реализуется только в отсутствии быстрых переходов.

На основе сделанных предположений была получена марковская цепь, которая реализовывалась с помощью метода Монте-Карло. В рамках этого метода нормально распределенная случайная величина задается наi-том шаге реализации процесса в момент времени на отрезке [0,1] и сравнивается с вычисленной вероятностью электронных переходов между ветвями КП. Если выполняется условие, реализуется электронный переход между ветвями КП. В ином случае определялась следующая случайная величина, которая сравнивалась с условной вероятностью туннельного перехода. По аналогии с предыдущим случаем, если, то реализуется туннельный переход, в другом случае определяется случайная величина. Примоделируется инактивационный переход, в противном случае вычисляется конформационная координата на текущем шаге по уравнению Ланжевена.

Повторяя описанную процедуру раз, гдеТ – длительность эксперимента, и вычисляя конформационную динамику на отрезках , на которых отсутствуют переходы, можно получить одну реализацию случайного процесса, которая является приближением исходного марковского процесса электронных и туннельных переходов.