
Подпоследовательности числовой последовательности
Пусть
(1) x1, x2, x3, .., xn , ..
Рассмотрим возрастающ последов номеров k1< k2< k3< ..< kn < ..
(2)
 ,
,
 ,
,
 ,
..,
,
..,
 ,
..
,
..
Числ послед (2) - это подпоследовательностью последовательности (1)
(3) x1, x3, x5, .., x2n-1 , ..
X2, x4, x6, .., x2n , ..
Заметим,
что k1
k2
> k1
k3
> k2
kn
Теорема о сходимости подпосл сходящихся последовательностей. Пусть последовательность Xn сходится к пределу a , тогда любая ее подпоследовательность сходится к пределу а.
Док-во:
Пусть {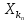 }
любая подпосл сходящийся последовательности
{Xn},
т.к. Xn
}
любая подпосл сходящийся последовательности
{Xn},
т.к. Xn
сходится
к пределу а
при n
 ,
то по определение предела
,
то по определение предела
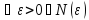 такой, что
такой, что
 выполняется для любого
выполняется для любого
 .
.
Если
 ⇒
kn
>
⇒
kn
>
 ⇒
⇒

Отсюда
следует, что подпослед { }
сход , причем
}
сход , причем
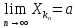 .
.
Следствие:
Отметим, что если из последоват можно извлечь 2 подпоследоват сходящиеся к разным пределам, то такая последоват расходится.
Действительно, если бы она сход к некотор пределу, то всевозможные её подпослед сход бы к одному и тому же пределу.
Монотонные последоват. Теорема Вейерштрасса о сходимости монотонной и ограниченной последоват.
Послед
{Xn}
наз-ся неубывающ если Xn+1
 Xn
Xn

Послед
{Xn}
наз-ся невозрастающей если Xn+1
 Xn
Xn

Послед {Xn} наз-ся монотонной если она либо невозраст либо неубыв.
Т-ма Вейерштрасса:
Если послед не убывает и ограниченна сверху то она сход.Если послед не возрастает и ограничена снизу то она сход. Д-во:
Рассмотрим
послед





 ,
,
 .
⇒
{Xn}
невозрастающ.
.
⇒
{Xn}
невозрастающ.
 при
при
 ,
то {Xn}
ограниченна снизу и следовательно по
т-ме Вейерштрасса она сходится.
,
то {Xn}
ограниченна снизу и следовательно по
т-ме Вейерштрасса она сходится.
 =
=
Обозначим
 ;
;
 ;
;
 ;
;

⇒
 .
.
Число е как предел последовательности.

Можно доказать что {Xn} не убывает и ограниченна сверх, по т-ме Вейерштрасса она сходится. Предел этой послед обазнач е
 ;
;


Фундаментальные последовательности. Критерии Каши сходимости числ послед
{Xn}
называется фундаментальной, если для
любого положительного числа
 такой , что
такой , что

 -натур
справедливо нер-во
-натур
справедливо нер-во
 .
.
Т-ма:
Числ послед {Xn} сходятся тогда и только тогда, когда она фундаментальна.
Док-во:
(ограничимся док-вом необходимости)
Пусть послед {Xn} сходится, докажем что в этом случае она фундаментальная.
Положим
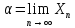
На
основании опр предела послед
 справедливо нер-во
справедливо нер-во
(1)
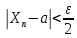
Пусть
n>N ,
тогда n+p>
N
,
тогда n+p>
N для
для
 -натур
-натур
(2)
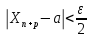 для
для

 -натур
-натур
Пусть
теперь n>
N
 +
+ =
= (для
(для
 -натур)
-натур)
Определение предела функции по Каши и Гейне. Эквивалентность этих определений.
Опр 1(Каши):
Число
b
будет наз пределом функции f(x)
при
 ,
если для
,
если для
 такое, что нер-во
такое, что нер-во
 , удовлетворяющего условию
, удовлетворяющего условию
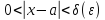
Опр 2 (Гейне):
Число
b
будет наз пределом функции f(x)
при
 ,
если для последоват значения аргумента
,
если для последоват значения аргумента
 удовлетворяет условию {Xn},
удовлетворяет условию {Xn},
 ,
,
 ,
,

Соответствующая
послед значения функции
 сходится к пределу b.
сходится к пределу b.
По Каши:





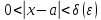
По Гейне:
{Xn}
 ,
,



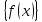
Опр пределов по Каши и по Гейне эквивалентны.
Теорема о пределе суммы, произведения и частного для функции.
Т-ма:
Пусть
 ,
,
 , тогда
, тогда
 при
x
при
x предел функции
предел функции
 ,
,
 .
Причем справедливы рав-ва
.
Причем справедливы рав-ва


Если
доп-но
 то сущ
то сущ

Причем справедливо рав-во

Док-во:
Ограничимся случаем суммы функций.
Обозначим
через b= и c=
и c= .
Пусть {Xn}
произвольная последоват значений
аргумента, которая удовлетворяет усл-ям
.
Пусть {Xn}
произвольная последоват значений
аргумента, которая удовлетворяет усл-ям
 ,
,
 ,
,
 .
.
Тогда
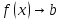 , а
, а
 c
, прия n
c
, прия n .
.
Но в этом случае на основании т-мы о пределе суммы для послед

Отсюда,
на основании опр Гейне о пределах
функции, следует, что

 и справедливо рав-во
и справедливо рав-во

Замечательные пределы.
Справедливы след соотношения
1)

2)

Бесконечно малые последовательности и функции
{Xn}
– будем наз бесконечно малой, если

 -
наз бесконечно малой при
-
наз бесконечно малой при
 ,
если
,
если

Опр сравнения беск мал:
Будем
говорить, что бесконечно малая
 является бесконечно малой более высого
порядка, чем
является бесконечно малой более высого
порядка, чем
 при
при
 , если
, если
 =0
=0
Опр эквив беск мал:
Бескон
мал
 и
и
 , при
, при
 наз эквивалентн, если
наз эквивалентн, если

 ,
,
 .
.
Теорема о замене бесконечно малой на эквив при вычисления предела:
При вычислении пределов произведений и частных бесконечно малую можно заменить на ей эквивалентную.
Предположим,
что
 и
рассмотрим выражения
и
рассмотрим выражения
 и
и

Справедливы
соотношения
 =
= и
и
 =
=
Если
 стремится к некоторому пределу b,
то поскольку
стремится к некоторому пределу b,
то поскольку
 из соотношения
из соотношения
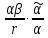 =
= следует, что
следует, что
 стремиться к тому же пределу b.
стремиться к тому же пределу b.
В сумме заменить бесконечно малую на эквивалентную НЕЛЬЗЯ.
Односторонние пределы.
Пусть
ф-ия
 определена на множестве Е и точка а
обладает св-вом : для любого положит
числа
определена на множестве Е и точка а
обладает св-вом : для любого положит
числа
 >0
(а;а+
>0
(а;а+ )
)
Опр правого предела:
Число
b
будем называть правым пределом функции
 в точке а
, если
в точке а
, если
 что
неравенство
что
неравенство
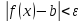 выполняется для любого х
выполняется для любого х Е такого что 0<x<a+
Е такого что 0<x<a+
Пусть
теперь а
такова,
что для любого
 на интервале (а-
на интервале (а- ;а)
содержит точки из Е.
;а)
содержит точки из Е.
Опр левого предела:
Число
b
называется левым пределом
 т.к. если
т.к. если

 так, что
так, что
 выполняется
для любого х
выполняется
для любого х Е удовл условию а-
Е удовл условию а- <x<а.
<x<а.
Понятие непрерывной функции.
Опр 1:
Будем
говорить, что
 непрерывна в точке a,
если
сущ
непрерывна в точке a,
если
сущ
 и справедливо
и справедливо
рав-во

Опр 2:
Будем
говорить, что
 непрерывна в точке a,
если
непрерывна в точке a,
если
 0
такое, что
0
такое, что


Опр 3:
Будем
говорить, что
 непрерывна в точке a,
если
для любой последовательности значений
аргумента {Xn}
удовлетв условию Xn
непрерывна в точке a,
если
для любой последовательности значений
аргумента {Xn}
удовлетв условию Xn при n
при n .
.
Теорема о непрерыв суммы, произвед и частного.
Т-ма:
Пусть
 непрерывна в точке a,
тогда их сумма (
непрерывна в точке a,
тогда их сумма ( ),
произведение (
),
произведение ( ),
и при дополн усл
),
и при дополн усл
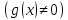 ,
частного
,
частного
 - непрерывна в точке а.
- непрерывна в точке а.
Док-во:
Ограничимся
случаем суммы. Т.к.
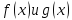 непрерывны в точке а , сущ
непрерывны в точке а , сущ


Тогда
по т-ме о пределе суммы сущ
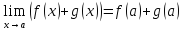 ⇒
⇒
непрерывна в точке а.
Понятие сложной ф-ии. Т-ма о непрерыв сложн ф-ии.
Пусть
y=f(t)
определена на множестве
 и пусть функция t=g(x)
определена на множестве E
, причем все её значения на Е не выходят
за пределы множества
и пусть функция t=g(x)
определена на множестве E
, причем все её значения на Е не выходят
за пределы множества
 .
.
Тогда на множестве Е определена сложная ф-ия F(x)=f(g(x))
Т-ма:
Пусть ф-ия t=g(x) непрерывна в точке x=a и ф-ия y=f(t) непрерывна в соответствующей точке b=g(a), тогда сложная ф-ия F(x)=f(g(x)) непрерывна в точке х=а.
Док-во:
Пусть
{Xn}
–произвольная послед аргументов х
удовлетворяющая условию Xn при n
при n .
Т.к. g(x)
непрерывна в точке а, то tn=g(Xn)
.
Т.к. g(x)
непрерывна в точке а, то tn=g(Xn)
 g(a)=b.
Т.к. tn
g(a)=b.
Т.к. tn
 b
при n
b
при n и f(t)
непрерывна в точке b
⇒
f(tn)
и f(t)
непрерывна в точке b
⇒
f(tn) ,
n
,
n ⇒
f(g(Xn))
⇒
f(g(Xn)) f(g(a)),
n
f(g(a)),
n .
.
F(Xn) F(a)
, n
F(a)
, n
 Значит, F(x)
непрерывна в точке х=а.
Значит, F(x)
непрерывна в точке х=а.
Точки разрыва ф-ии. Классиф точек разрыва.
Опр разр 1 рода:
Говорят,
что в точке а
 имеет разрыв 1-го рода, если в этой точке
сущ оба односторонн предела
имеет разрыв 1-го рода, если в этой точке
сущ оба односторонн предела
 ,
,



Опр разрыв 2-го рода:
Говорят,
что в точке а
 имеет разрыв 2-го рода, если хотя бы один
из односторон пределов в этой точке не
сущ.
имеет разрыв 2-го рода, если хотя бы один
из односторон пределов в этой точке не
сущ.
Пример:

Понятие производной. Таблица производных основных элементарных ф-ий.
F(x)
(a;b)
x0 (a;b)
Дадим аргументу приращение
(a;b)
Дадим аргументу приращение
 ⇒
x0+
⇒
x0+
 считать
столь малым, что x0+
считать
столь малым, что x0+ (a;b)
(a;b)

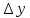 –приращение
аргумента в точке
–приращение
аргумента в точке
 , отвечающее прирощению аргумента
, отвечающее прирощению аргумента


Предел
разностного отношения
 при
при
 (если он существует) называется
производной рассматриваемой ф-ии
(если он существует) называется
производной рассматриваемой ф-ии
 в точке
в точке
 .
.
Таблица производных основных эл ф-ий:
С’=0











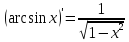



Понятие дифференцируемой ф-ии. Критерии диф-сти.
Опр:
Будем
говорить , что ф-ия у= диффир-ма в точке
диффир-ма в точке
 , если ее приращение
, если ее приращение
 в этой точке, отвечающее приращению
аргумента
в этой точке, отвечающее приращению
аргумента
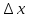 представимо в виде
представимо в виде
 =А*
=А* +а(
+а( , где А=const,
a(
, где А=const,
a( 0 при
0 при
 0
0
Т-ма Критерии диф-сти:
у= дифф-ма в точке х0
тогда и только тогда, когда сущ производная
дифф-ма в точке х0
тогда и только тогда, когда сущ производная
 .
.
Д-во:
Пусть
 диф-ма в точке х0
тогда для её приращения
диф-ма в точке х0
тогда для её приращения
 справедливо представление
справедливо представление
 =А*
=А*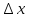 +а(
+а( ;
a(
;
a( 0;
0;
 0.
0.
Верно
на основании определения
 a(
a( .
.
Правая
часть рав-ва стремящаяся к пределу А,
при
 0 ⇒
существует
0 ⇒
существует
 =А
⇒
=А
⇒
сущ
 и кроме того доказано что
и кроме того доказано что
 =А.
=А.
Предположим
теперь, что сущ
 .
.
Обозначим
a( =
= -
-
 Т.к. при
Т.к. при
 0
0

 , то правая часть соотношения a(
, то правая часть соотношения a( =
= -
-
 стремится к 0, при
стремится к 0, при
 0 ⇒
a(
0 ⇒
a( 0,
0,
 0.
0.
а(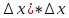 =
= -
-
 =
= +
а(
+
а(
 =
= +
а(
+
а( при а(
при а( )
) 0 и
0 и
 0
0
A=
⇒ у= диф-ма в точке
диф-ма в точке
 . Если
. Если
 диф-ма в точке
диф-ма в точке
 ее приращ
ее приращ
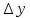 в этой точке отвечающие прирощению
аргумента
в этой точке отвечающие прирощению
аргумента
 ровняется
ровняется
 =
= +
а(
+
а( при а(
при а( )
) 0 и
0 и
 0
0
 ⇒
⇒
 явл
бесконечно малой более высокого порядка
чем
явл
бесконечно малой более высокого порядка
чем

 =
= .
.
 =
=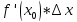 +
+ ,
если
,
если
 -диф-ма в точке
-диф-ма в точке
 .
.
Из
рав-ва
 =
= +
+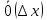 следует
следует


Это
означает, что
 ,
,
 .
.
 ;
;

 при
при

 ⇒ Если
⇒ Если
 диф-ма в точке
диф-ма в точке
 , то она непрерывна.
, то она непрерывна.
Обратное неверно.
Т-ма о диф-ии суммы, произведения и частного.
Пусть
u(x),
v(x)
диф-мы в точке
 , тогда u(x)+v(x),
u(x)*v(x)
и при условии (v(x0)
, тогда u(x)+v(x),
u(x)*v(x)
и при условии (v(x0) )
частное
)
частное
 так же диф-мо в точке
так же диф-мо в точке
 . Причем справедливы соотношения
. Причем справедливы соотношения
(u+v)’( =u’(
=u’( +v’(
+v’( )
)
(uv)’( )=
u’(
)=
u’( v(
v( )+
u(
)+
u( v’(
v’( )
)

Док-во(для суммы):
y=u(x)+v(x)
 =u(
=u( )+v(
)+v( )-u(
)-u( )-v(
)-v( )=
)=
 +
+



Т.к.
u(x)
и v(x)
диф в точке
 , то
, то
 ),
),
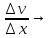 v’(
v’( ),
),

Отсюда
и из
 ⇒
что сущ предел правой части рав-ва
⇒
что сущ предел правой части рав-ва
 ⇒
и левой.
⇒
и левой.
Значит
y=u(x)+v(x)
диф в точке
 .
Переходя теперь в
.
Переходя теперь в
 к пределу при
к пределу при
 получаем (u+v)’(
получаем (u+v)’( )=u’(
)=u’( )+v’(
)+v’( ).
).
Док-во(для произв):
y=u(x)v(x)
 =u(
=u( )v(
)v( )-u(
)-u( )v(
)v( )=
)=
u( )v(
)v( )-
u(
)-
u( )
v(
)
v( )+
u(
)+
u( )
v(
)
v( )-
u(
)-
u( )v(
)v( )=
)=
v( )
)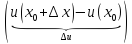 +
+
u( )(
v(
)(
v( )-
v(
)-
v( ))=v(
))=v( )
) +
u(
+
u( )
)

Т.к.
ф-я v(х)
диф в точке
 , то
, то
 v(
v( )
,
)
,
 .
.
Т.к.
у= u(x)v(x)
диф ⇒
она непрерывна в точке
 ⇒
⇒
Сущ предел правой, а следовательно и левой части рав-ва

у=
u(x)v(x)
диф в точке

переходя в рав-ве к пределу получаем
(uv)’( )=
u’(
)=
u’( v(
v( )+
u(
)+
u( v’(
v’( ).
).
Док-во(для частного):
y= ;
;
 =
=
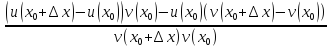 =
=

y= ;
;

Т.к.
u(x)
и v(x)
диф в точке
 , то
, то
 ),
),
 v’(
v’( ),
),

Т.к.
ф-я v(х)
диф в точке

 v(
v( )
,
)
,
 .
.
⇒ Сущ предел правой, а следовательно и левой части рав-ва

⇒ y= диф в точке
диф в точке

Переходя теперь в рав-ве

К пределу, получаем

