2.Т. Вейерштрасса о достижимости точных грней для непрерывной функции

Пусть ф-я f(x) непрерывна на [a,b], тогда она достигает на этом сигменте своей точной верхней и точной нижней грани, т.е сущ. точки и [a,b] такие , что f() = sup_[a,b]f(x)

Док-во. Проведем док-во для точной верхней грани.. Обозначим через M = sup_[a,b]f(x) (точная верхняя грань функции f(x) на [a,b] сущ. по 1 т. Вейер...).Итак, предположим противное. Точная верхняя грань f(x) на [a,b] не достигается на этом сигменте, тогда f(x) < M в любой x [a,b]. Введем в рассмотрение ф-ю g(x) = . Ф-я g(x) непрерывна на [a.b], стогда по 1 т Вейер.. g(x) огранич на [a,b] , сл сущ положительная константа c такая, что . с в любой . 1 с(М – f(x)). м - в любой . Это противоречит тому, что Vявляется точной верхней гранью ф-ии f(x) на [a,b].

1.Т. Вейерштрасса

Пусть ф-я f(x) непрерывна на [a,b], тогда она ограничена на этом же сигменте.

(В ЛЕКЦИЯХ НЕ БЫЛО ДОК-ВА)

Точная верхняя и точная нижняя грань функци на мн-ве

Точной верхн. и точн. нижней гранью функции f(x) на мне E будем называть точную верхнюю грань числового мн-ва , образованного всевозм значениями ф-ии f(x) , когда x E sup_Ef(x) = sup{f(x),xE} .точной нижней гранью ф-ии f(x) на мн. E называется точная нижняя грань чилового мн-ва, образ всевозм значениями ф-ии f(x) , когда x E inf_E f(x) =inf{f(x), x E}

Точные грани числовых мн-в

Пусть E некоторое подмн-ва числовой прямой. 1) мно-во E называют огр сверху, если сущ число M такое, что x ≤ M при любом xE. Число M в таком случае называется верхней гранью мн-ва E. Отметим, что если точка М явл верхней гр мн-ва Е, то любое число, превосходящее М так же будет верхней гранью Е. 2)Мн-во Е называют огран снизу, если сущ ≥число м такое, что х≥м для любого xE. Такую точку м называют нижней гранью мн-ва Е.Отметим, что если м-нижняя грань Е, то любое число меньше м так же будет нижней гранью Е.

Определение. Мн-во Е называют огран. Если оно огран как сверху так и снизу.

Точной верхней гранью мн-ва Е называется наименьшая из верхних граней этого мн-ва.Пусть a=supE, тогда для а выполнены ус-я : 1) х≤ф при любом x E 2)любое а’<a, сущ x’ E такая, что a’<x’.Наоборот, если для ф выполнены усл-я (1) и (2), то а = supE.

Определение. Точной гранью мн-ва Е называется наибольшая из нижних граней этого мн-ва. Пусть а = infE, тогда для а вып усл : 3) х≥а при любом x E 4) любое а’>a, сущ x’ E такая, что a’>x’. Если для точки а вып. усл-я (3) и (4), то а = infE

Теорема о сущ. точных граней

Пусть мн-во не пусто и огран. Сверху, тогда у этого мн-ва сущ точная верхняя грань. Пусть мн-во не пусто и огр снизу, тогда у этого мн-ва сущ точня нижняя грань.

Теорема о промежуточном значении непрерывной ф-ии

Пусть ф-я f(x) непрерывна на [a,b] и на концах этого сигмента принимает неравные значения. Тогда для любого числа , заключенного между f(a)≠f(b) найдется точка с, принадлежащая интервалу [a.b] такая, что f(c) =

Док-во. Предположим для определенности, что f(a)<f(b), возьмем любое 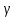. f(a)<) <f(b). Введем в рассмотрение ф-ю g(x)=f(x)- , g(x) непрерывна на [a,b] ( т.к f(x) обладает этим св-ом) При чем g(a) =f(a) - <0, g(b)=f(b)- >0. Отсюда на осн теоремы об обращении в 0 непрерывной ф-ии => что сущ с [a,b] такая, что g(c) =0 => g(c)=f(c)-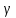 =0 => f(c)=

Т-ма об обращении в ноль непр. ф-ии.

Пусть f(x) непрерывна на [a,b] и на концах сигмента принимает знач-ия разных знаков, тогда сущ с любому? (a,b) такая, что f(c) = 0 , f(a) <0, f(b) . 0, sup{x[a,b] , f(x) < 0} = c

Док-во. Предположим для опр-ти, что f(a) <0, f(b)>0. Обозначим чрез Е = {x[a,b].f(x)<0}.Мн-во Е не пусто (ему принадлежит точка а и ограничена сверху. Одной из верхних граней является например точка b). => сущ. точная верхняя грань этого мн-ва. Положим с = sup E . Точка с не может совпадать с точками a или b, т.к сущ ∂>0, такое , что при изм-ии арг. x в правой ∆-полуокрестности точка а f(x)<0 и при изм-ии арг-та x в левой ∆-полуокрестности точка b f(x)>0 => a<c<b. Положим противное. В точке с f(x) изменим зна-ия опр. знака, тогда найдется такая ∆-окр-ость в с в интервале (с - ∂, с +∂)при изменении арг. x в пределах которой f(x) сохр. знак.Это противоречит следующему по с-вам точной верхней грани f(x) ≥0 для c <x<c+∂ и сущ. x ( c

- ∂, c), такого, что f(x) < 0

Т-ма об устойчивости знака непрерывной ф-ии

Пусть f(x) определена на мн-е E и непрерывна в некоторой точке a этого мн-ва, причем f(a)>0 (f(a)<0), тогда найдется такая окрестность в точке а (a -, a+), что для значений xE (a -, a+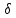) справедливо неравенство : f(x)>0 (f(x)<0). Доказательство. Пустьf(a)>0. Положим . Т.к ф-я f(x) непрерывна в точке а, то сущ >0, что неравенство выполняется для любого x из E, удовоетвор условию : |x-a|<. => f(a)- < f(x)<f(a)+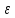 для любого x из E, удовлетвло условию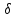: a-<x<a+.Отсюда получаем для всех xE (a -, a+).

Интегрирование по частям

Пусть ф-ии u(x) и v(x) имееют непрерывные производные u’(x) и v’(x) в некотором промежутке (u(x)*v(x))’=u’(x)*v(x)+u(x)*v’(x); u(x)*v’(x) = (u(x)*v(x))’-v(x)* u’(x), тогда = ; ; ; .

ФОРМУЛА

Замена переменной в неопр. интеграле.

Пусть , тогда

Док-во. F(g(x))’ = проверим второе из соотношений диф правой части (*) ≈

Таблица основных интегралов

1)

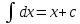
2)

3)

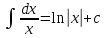
4)

5)

6)=tgx+c

7)

8)

9)=

10)

11)

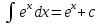
12)

13)

Простейшие св-ва неопр. интеграла

1)

2)

Док-во. Пусть F(x) первообразная для f(x), а G(x) для g(x), тогда . Утверждение 2 док-ся аналогично

Понятие первообразной неопр интеграла

Ф-ю F(x) будем называть первообразной ф-ии f(x) в некотором интервале, если всюду в этом интервале F’(x)=f(x)

Очевидно, что если F(x) первообразная для f(x), то любая ф-я вида F(x) +c, где с-постоянная так же будем первообразная для f(x).

можно док-ть, что мн-ва функций F(x)+c, где с произвольная постоянная является совокупностью всех первообразных данной функции f(x)

Определение неопределенного интеграла

Совокуность всех первообразных функций f(x) называется ее неопределенным интегралом и обозначается так

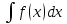
Если F(x) произвольная первообразная для f(x), то , где с = const.

Дифференциал функции

Пусть ф-я y=f(x) диф в некоторой точек x, тогда ее приращение ∆y в этой точке, отвечающее приращ. аргумента ∆x может быть представлено в виде : ∆y = f’(x) * ∆x+ (∆x)

Определения диф в рассматр точке x. Линейную часть f’(x)* ∆x приращ ф-ии y=f(x) в точке x будем называть деф этой функции в данной точке x d(f(x))=f’(x)* ∆x dy=f’(x) ∆x

Положим dx=∆x и нах dx диф независимой переменной, тогда df(x)=f’(x)dx dy=f’(x)dx

Производные высших порядков

Пусть ф-я y=f(x) диф. в нек. интервале 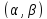, тогда первая произв f’(x) так же явл. функцией, определенной на эом интервале. Если в какой-то точке x из этого интервала первая пр. f’(x) диф, то ее производную в этой точке называют производной 2-го порядка исходной ф-ии y=f(x) в рассматр. точке. Аналогично орп. производные 3-го, 4-го порядка и тд. Если производная (n-1) уже определена, то производная n-го порядка вводится соотношением

Теорема о диф. обратной ф-ии

Пусть ф-я y=f(x) монотонно возрастает (или убывает) непрерывна в некоторой окрестности точки . Пусть далее ф-я y=f(x) диф. в точке при чем f’(0, тогда в нек. окр. соотв. точки =f() определена обратная ф-я которая диф в точке ,при чем справедливо р-во ;( = (*)

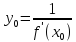y=tg x , x (- ) ; x=arctg x ; (*) =

Понятие обратной ф-ии

Пусть ф-я y=f(x) определена на мн-ве X и Y –мн-во ее значений. Предположим, что для любого y Y сущ. единственное xX такое, что y = f(x). Тогда на мн-ве Y будем определена некоторая ф-я, которую называют обратной для ф-ии y=f(x) и обозначают x=.

Теорема о диф сложной ф-ии

Пусть ф-я t=g(x) диф. в точке , а ф-я y=f(t) диф в соотв. точке =g(), тогда сложная ф-я F(x)=f(g(x)) диф в точке , при чем справедливо соотношение F’()=f’(g())*g’).

Док-во

Итак дадим аргументу x в точке приращение ∆x. Положим ∆t=g( + ∆x) – g(). Через ∆y обозначим: ∆y=f(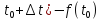 ; . Т.к ф-я y=f(t) диф в точке , то для ее приращения ∆y в этой точке справедливо приращение(1) , т.е ∆y явл. приращением сложной ф-ии y=F(x) в точке , отв. приращ аргумента 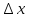, сл из соотн (1) получаем 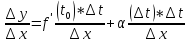, , т.к ф-я t=g(x) диф в так же 0, 0 и => . Отсюда следует, что сущ предел правой части (1) при 0 , значит сущ предел и левой части => ф-я F(x) диф в точках. при 0 получаем следующее и