Предел числовой последовательности. (пчп)
Пусть каждому натуральному числу n поставлено ненатуральное вещественное число Xn , тогда говорят, что задана последовательность n с числом Xn .
Xn=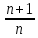 =1+
=1+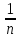
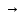 1 , n
1 , n
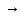
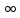 ;
;
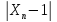 =
=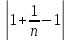 =
=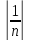 ;
;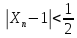 ;
;
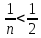 ; n
; n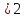 ;
;
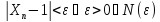 ;
;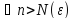 .;
∀
.;
∀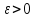 ;
;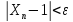 ;
;
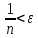 ;
1
;
1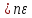 ;
;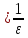
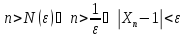
В
качестве N(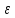 )
можно взять любое натуральное число
больше
)
можно взять любое натуральное число
больше
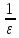 .
.
ПЧП
—число a
будем называть пределом последовательности
Xn
при n
стремящемся к бесконечности, если для
любого положительного числа
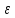 существует N(
существует N(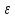 )
такой, что
)
такой, что
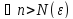 справедливо неравенство
справедливо неравенство
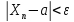
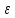 -окрестности
точки a
будем
называть интервал (а-
-окрестности
точки a
будем
называть интервал (а-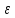 ; а+
; а+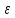 )
)
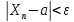
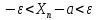
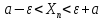
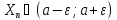
2-Опр. ПЧП:
Число
а
называется
пределом последовательности Xn
при n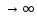 ,
если любая
,
если любая
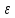 окрестности а содержит все числа
рассматриваемой последовательности,
начиная с некоторого номера.
окрестности а содержит все числа
рассматриваемой последовательности,
начиная с некоторого номера.
Числовую последовательность Xn называют сходящийся, если существует число а, являющаяся пределом этой последовательности, в противном случае последовательность является расходящейся.
Теорема: Предел сходящейся последовательности единственен.
{Xn}
, a≠b, a=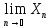 ,
,
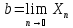
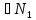
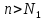
N0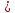 nmax
{N1;N2}
n0
nmax
{N1;N2}
n0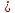 N1
n0
N1
n0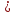 N2
Док-во:
Предположим противное, предел
последовательности Xn
не единственен, тогда существует 2 числа
a≠b
такие что a=
N2
Док-во:
Предположим противное, предел
последовательности Xn
не единственен, тогда существует 2 числа
a≠b
такие что a=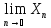 и
и
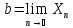 (для определенности будем считать, что
а
(для определенности будем считать, что
а b).(1)
Выберем
b).(1)
Выберем
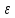 окрестности точек a
и b
так, чтобы они не пересекались, т.е.
чтобы
окрестности точек a
и b
так, чтобы они не пересекались, т.е.
чтобы
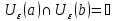 .(Для
этого очевидно
.(Для
этого очевидно
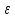 надо подобрать так, чтобы
надо подобрать так, чтобы
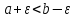 ;
;
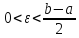 )Из условия следует, что существуют
такие номера N1
и N2,
что Xn
)Из условия следует, что существуют
такие номера N1
и N2,
что Xn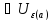 ,Когда
n
,Когда
n N1,
и Xn
N1,
и Xn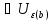 , когда n
, когда n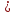 N2
.n0
N2
.n0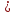 max{N1,N2},
тогда
max{N1,N2},
тогда
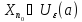 ;
;
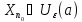 Что противоречит (1)Получаем противоречие
доказывающие теорему.
Что противоречит (1)Получаем противоречие
доказывающие теорему.
Теорема о пределе суммы, произведения и частного сходящихся последовательностей.
Пусть {Xn} и {Yn} – числ. последовательности.
(1) x1, x2, x3, .., xn , ..
(2)y1, y2, y3, .. , yn , ..
Последовательности
(3) x1+y1 , x2+y2, x3+y3, .. , xn+yn , ..
(4) x1y1 , x2y2, x3y3, .. , xnyn , ..
(5)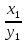 ,
,
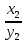 ,
,
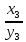 ,
.. ,
,
.. ,
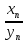 ,
..
,
..
будем называть суммой, произведения и частным.
Т-ма:
1.Пусть Xn и Yn – сходящиеся последовательности, тогда их сумма и произведение также являются сходящимися последовательностями, причем
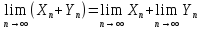
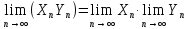
2.Если
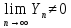 ,
то последовательность
,
то последовательность
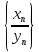 сходятся, причем
сходятся, причем
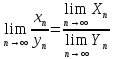
Д-во:
Ограничимся случаем суммы последовательности.
Пусть
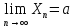 ,
,
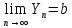 .
.
На
основании определения предела
последовательностей
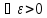 сущ. N
такие, что (1)
сущ. N
такие, что (1)
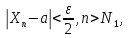 Обозначим через N=max{N1,N2}
Обозначим через N=max{N1,N2}
(2)
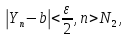 тогда для
тогда для
 выполняется одновременно неравенства
(1) и (2).
выполняется одновременно неравенства
(1) и (2).
Далее
получаем, если n>N,
то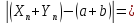
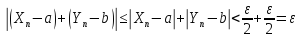
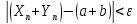 ,
n>N.
,
n>N.
Переход к пределу в неравенстве.
Теорема:Пусть
{Xn}
и {Yn}
–сходящиеся последовательности, причем
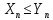 для n>m,
тогда
для n>m,
тогда
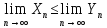 ,
,
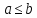 .
.
Док-во:Обозначим
a=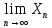 и b=
и b= .
Надо доказать, что
.
Надо доказать, что
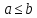 .Предположим
противное a>b.
Зафиксируем число
.Предположим
противное a>b.
Зафиксируем число
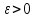 столь малым, чтобы выполнилось неравенство
столь малым, чтобы выполнилось неравенство
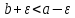 (чтобы окрестности не пересекались)Тогда
на основании определения предела сущ
N1,
N2
такие, что
(чтобы окрестности не пересекались)Тогда
на основании определения предела сущ
N1,
N2
такие, что
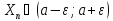 ,
n>N1
и
,
n>N1
и
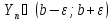 ,
n>N2
,
n>N2
Выберем
n0>max(N1,N2,m),
тогда очевидно
 ;
;
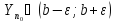 .
.
=>
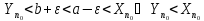 - противоречит условию.
- противоречит условию.
Отметим,
что для сход последовательностей
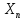 и
и
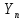 из строгого неравенства
из строгого неравенства
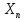 <
<
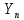 ;
n>m
не следует строгое неравенство между
пределами этих последовательностей.
Следовательно при переходе к пределу
в строгом неравенстве надо заменить
знак строго нер-ва на знак не строгого
нер-ва.
;
n>m
не следует строгое неравенство между
пределами этих последовательностей.
Следовательно при переходе к пределу
в строгом неравенстве надо заменить
знак строго нер-ва на знак не строгого
нер-ва.
Пусть
последовательность {Xn},
{Yn},
{Zn}
таковы, что Xn
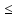 Yn
Yn
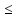 Zn
;
n>m.
Zn
;
n>m.
Тогда,
если
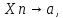 при
n
при
n
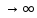
Yn
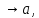 при
n
при
n
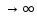 ,
то в этом случае
,
то в этом случае
Zn
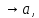 при
n
при
n