
Формула
ТейлораТеорема.
Пусть ф-я f(x)
в некоторой окр. точка а имеет производные
до (n-1)
порядка включительно и кроме того в
самой точке а сущ. производная n-го
порядка f(n)(а)
, тогда для рассматриваемой функции
f(x)справедливо
предст
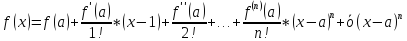
Разложения
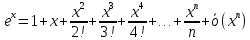

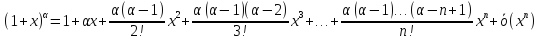
Правила
Лопиталя 1)Пусть
функции f(x)
и g(x)
определены и диф. В некоторой проколотой
(∂-дельта) ∂ окрестности точки a
у Ů∂ (а) (это проколотая ∂ окрестность
точки а) при чем g’(x)≠
0 для x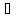 Ů∂ (а)
Ů∂ (а)
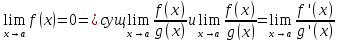
Доказательство
. Доопределим
ф-ии f(x)
и g(x)
в а , положив f(a)
= 0 и g(а)
= 0, тогда f(x)
и g(x)
(после доопределения) становятся
непрерывными в точке а. Обозначим теперь
через
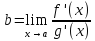 .
Пусть xn
произвольная
посл-ость значений аргумента, уд. Условию
xn
.
Пусть xn
произвольная
посл-ость значений аргумента, уд. Условию
xn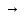 а,
n
а,
n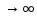 и xn
и xn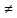 а при любом n.
Рассмотрим [а, xn].
Функции f(x)
и g(x)
уд. условию на этом сигменте по т. Каши
тогда ущ. Точка сn
а при любом n.
Рассмотрим [а, xn].
Функции f(x)
и g(x)
уд. условию на этом сигменте по т. Каши
тогда ущ. Точка сn
 (а,
xn)
такая, что
(а,
xn)
такая, что
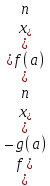 , отсюда следует
, отсюда следует
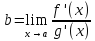 . (1)
. (1)
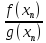 =
=
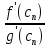 ,при
,при
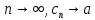 =>
=>
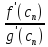 =>
=>
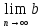 ,
но тогда из (1) следует, что
,
но тогда из (1) следует, что
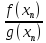 =>
=>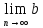 .
На лсновании опр. Тейлора предела
функции это означает, что
.
На лсновании опр. Тейлора предела
функции это означает, что
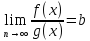 ]
2)Пусть
ф-ии f(x)
и g(x)
определены и диф. В некоторой проколотой
(∂-дельта) ∂ окрестности точки a
у Ů∂ (а) и кроме того
]
2)Пусть
ф-ии f(x)
и g(x)
определены и диф. В некоторой проколотой
(∂-дельта) ∂ окрестности точки a
у Ů∂ (а) и кроме того
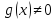 в любой
в любой
 Ů∂ (а). пусть далее
Ů∂ (а). пусть далее
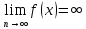 и
и
 ,
тогда если сущ.
,
тогда если сущ.
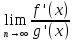 То
сущ.
То
сущ.
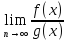 и справедливо равенство
и справедливо равенство
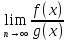 =
=

Теорема Каши
Пусть
ф-я f(x),g(x)
непрерывны на [a;b]
диф в (а,в) при чем
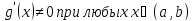 тогда сущ. с
тогда сущ. с
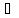 (а,в)
такая, что
(а,в)
такая, что
 =
=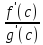
Доказательство
Заметим,
что g(b)
≠ g(a)
( действительно если бы g(b)=g(a),
то нашлась бы точка x0
в(а,в) такая, что g’(x0)=0
по т.Ролля, а это противоречит
условию).Введем в рассмотрение функцию
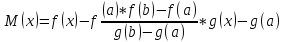 . Ф-я F(x)
непрерывна на [a,b]
и диф. В
(a,b), кроме
того
F(a)=0 и
F(b)=0
. Ф-я F(x)
непрерывна на [a,b]
и диф. В
(a,b), кроме
того
F(a)=0 и
F(b)=0
f(b)-f(a)
-
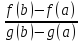 * (g(b) – g(a)) => F(b) = 0. Ф-я
F(x)
на [a,b]
уд. всем условиям т. Ролля, сл сущ. точка
c
* (g(b) – g(a)) => F(b) = 0. Ф-я
F(x)
на [a,b]
уд. всем условиям т. Ролля, сл сущ. точка
c
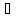 (a,b)
такая, что F’(c)
= 0. (1) F(x)
=
(a,b)
такая, что F’(c)
= 0. (1) F(x)
=
 . Из (1) получаем F’(x)
= f’(x)
-0-
. Из (1) получаем F’(x)
= f’(x)
-0-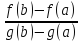 *g’(x)
=> F’(c)
= 0 = f’(c)
-
*g’(x)
=> F’(c)
= 0 = f’(c)
-
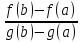 * g’(c)
=>
* g’(c)
=>
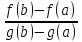 =
=
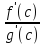
Условия монотонности ф-ии на интервале
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Т-ма об усл-ях монотонности ф-ии на интервале.
Пусть
f(x)
диф на (a,b),
причем f’(x)>0
(f’(x)<0)
в любом x
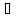 (a,b),
тогда f(x)
монотонно возрастает(убывает) в (a,b).
(a,b),
тогда f(x)
монотонно возрастает(убывает) в (a,b).
Док-во.
Пусть например f’(x)
>0 в любом x
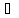 (a,b).
Введем
(a,b).
Введем
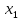 и
и
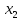 такие, что
такие, что
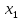 и
и
 лежат в (a,b),
лежат в (a,b),
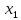 <
< , ф-я f(x)
на [a,b]
удовлетворяе усл-ям т.Лагранжа =Ю сущ.
с
, ф-я f(x)
на [a,b]
удовлетворяе усл-ям т.Лагранжа =Ю сущ.
с
 (a,b)
такая, что f(
(a,b)
такая, что f(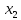 )
– f(
)
– f(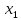 )
= f’(0)(
)
= f’(0)(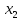 -
-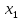 ).
Т.к f’(c)
> 0 ,
).
Т.к f’(c)
> 0 ,
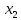 -
-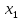 >0
=> f(
>0
=> f(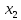 )
– f(
)
– f(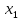 )>0
=> f(
)>0
=> f(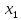 )<
f(
)<
f(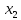 )
)
Теорема о постоянстве функции произведение которой тождественно равно нулю
Пусть
ф-я f(x)
диф в (a,b),
причем f’(x)=0
при любом x
 (a,b),
тогда f(x)
постоянна в (a,b).
(a,b),
тогда f(x)
постоянна в (a,b).
Док-во.
Зафиксируем нек. точку

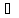 (a,b).
Пусть x
– любая др. точка этого интервала. f(x)
удовлетворяет всем усл-ям т-мы Лагранжа
на сегменте [
(a,b).
Пусть x
– любая др. точка этого интервала. f(x)
удовлетворяет всем усл-ям т-мы Лагранжа
на сегменте [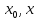 ].
По т. Лагранжа сущ с
].
По т. Лагранжа сущ с
 (
(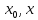 )
такая, что f(x)
– f(
)
такая, что f(x)
– f(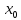 )
= f’(c)
* (
)
= f’(c)
* (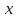 -
-
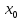 ).
f’(c)
= 0. f(x)
– f(
).
f’(c)
= 0. f(x)
– f(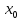 )=0
, f(x)
= f(
)=0
, f(x)
= f(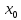 )
для всех x
)
для всех x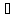 (a,b)
(a,b)
Теорема Лагранжа
Пусть
ф-я f(x)
непрерывна на [a,b]
и диф. В (a,b),
тогда сущ. точка с
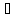 (a,b)
такая, что f(b)
– f(a)
= f’(c)
* (b-a)
(a,b)
такая, что f(b)
– f(a)
= f’(c)
* (b-a)
Док-во.
Введем в рассмотрение функцию g(x),
опр. Сл. Образом
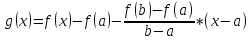 .
.
Ф-я
g(x)
непрерывна на [a,b]
и диф в (a,b).
g(a)=0
(если подставить точку a).
G(b)
=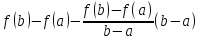 =f(b)-f(a)-(f(b)-f(a))=0.
Сл.
g(x)
удовлетворяет на [a,b]
всем условиямт.Ролля. Тогда сущ. точка
с
=f(b)-f(a)-(f(b)-f(a))=0.
Сл.
g(x)
удовлетворяет на [a,b]
всем условиямт.Ролля. Тогда сущ. точка
с
 (a,b)
такая, что g’(c)=0
(!1!). Из (1) следует:
(a,b)
такая, что g’(c)=0
(!1!). Из (1) следует:
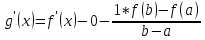 => g’(c)=0=
=> g’(c)=0=
=f’(c)-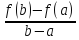 ,
,
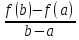 =f’(c)
, f(b)-f(a)=
=f’(c)
, f(b)-f(a)=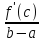
Теорема Ролля.
Эта теорема позволяет отыскать критические точки, а затем с помощьюдостаточных условий исследовать ф-ю на экстремумы.
Пусть
ф-я f(x)
непрерывна на [a,b],
диф в (a,b)
, при чем f(a)
= f(b),
тогда cущ.
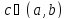 такая, что f’(c)
=0
такая, что f’(c)
=0
Доказательство
Обозначим через m и M точнюю нижнюю и точную верхнюю грань функции f(x) на сигменте [a,b], тогда
1
случай. m≤F(x)
≤M
в любой точке x,
рассматриваемого сигмента (m≤M).
1 случай m=M
=>и из (1) , что f(x)=m=M
в любой точке х, рассматриваемого
промежутка (a,b)
любого x
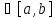 .
В этом случае в качестве точки с можно
взять любую точку из (a,b)
т.к рассматриваемая ф-я постоянна и
произв. ее = о). 2 случай. Пусть m<M,
тогда по 2 т. Вейерштрасса точные грани
m
и M
достигаются на сигменте (a,b),
при чем в силу условия f(a)=f(b)
хотябф 1 из точных граней (пусть например
M)
достигается в интервале (a,b),
сущ .
.
В этом случае в качестве точки с можно
взять любую точку из (a,b)
т.к рассматриваемая ф-я постоянна и
произв. ее = о). 2 случай. Пусть m<M,
тогда по 2 т. Вейерштрасса точные грани
m
и M
достигаются на сигменте (a,b),
при чем в силу условия f(a)=f(b)
хотябф 1 из точных граней (пусть например
M)
достигается в интервале (a,b),
сущ .
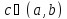 такая, что f(c)=M
=> , что в точке с ф-я f(x)
имеет локальный максимум => по т.Ферма
f’(c)
=0
такая, что f(c)=M
=> , что в точке с ф-я f(x)
имеет локальный максимум => по т.Ферма
f’(c)
=0
Локальный экстремум.Необходимое ус-е локального экстремума.
Ф-я
f(x)
имеет локаьный экстремум в точке
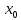 ,
если найдется такая окрестность в точке
,
если найдется такая окрестность в точке
 в пределах которой значения f(
в пределах которой значения f(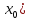 является максимальным. 1. Будем
говорить, что ф-я f(x)
имеет лок. Минимум в точке
является максимальным. 1. Будем
говорить, что ф-я f(x)
имеет лок. Минимум в точке
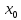 ,
если найдется такая окрестность
,
если найдется такая окрестность
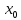 в пределах которой знач.f(x)
является мин. 2. Будем говорить, что ф-я
f(x)
имеет в
в пределах которой знач.f(x)
является мин. 2. Будем говорить, что ф-я
f(x)
имеет в
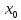 локальный экстремум, если она имеет в
этой точке либо локальный максимум,
либо лок. минимум.
локальный экстремум, если она имеет в
этой точке либо локальный максимум,
либо лок. минимум.
Теорема Ферма. (необходимое услоие лок. экстремума)
Пусть
ф-я f(x)
диф. В точке
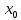 и
имеет в этой точке лок. экстремум, тогда
f’(
и
имеет в этой точке лок. экстремум, тогда
f’(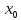 )
= 0
)
= 0
