Тот факт, что оптимальное решение находится в одной из вершин многоугольника одр, позволяет сделать еще два важных вывода:

если оптимальным решением являются координаты вершины многоугольника ОДР, значит, сколько вершин имеет ОДР, столько существует целевых функций и столько оптимальных решений по этим функциям может иметь задача.

 поскольку, чем больше ограничений имеет задача, тем больше вершин, тo, следовательно, чем больше целевых функций и, следовательно, тем больше оптимальных решений по этим функциям.

Из рисунков можно сделать вывод, что вершина, координаты которой являются оптимальным решением, определяются углом наклона прямой, описывающей целевую функцию. Значит, каждая вершина будет соответствовать оптимальному решению для некоторой целевой функции. Итак, нахождение решения задачи линейного программирования (5.8)-(5.10) на основе ее геометрической интерпретации включает следующие этапы.

Этапы нахождения решения задачи линейного программирования:

 Строят прямые, уравнения которых получаются в результате замены в ограничениях (5.9) и (5.10) знаков неравенств на знаки точных равенств.

 Находят полуплоскости, определяемые каждым из ограничений задачи.

 Находят многоугольник решений (ОДР).

 Строят вектор C=(с₁; с₂).

 Строят прямую c₁x₁+c₂x₂=h, проходящую через многоугольник решений.

 Передвигают прямую c₁x₁+c₂x₂=h в направлении вектора С, в результате чего-либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.

 Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

5.3. Графическое решение задачи распределения ресурсов

Пусть для двух видов продукции П₁ и П₂ требуются трудовые, материальные и финансовые ресурсы. Наличие ресурсов каждого вида и их нормы расхода, необходимые для выпуска единицы продукции, приведены в табл. 5.1.

Таблица 5.1

Характеристика	Вид продукции		располаг.
	П1	П2	ресурс
Резервы:
трудовые	1	4	14
материальные	3	4	18
финансовые	6	2	27
выпуск	1	1	---
прибыль	4	8,5	---
план	х1	х2	---

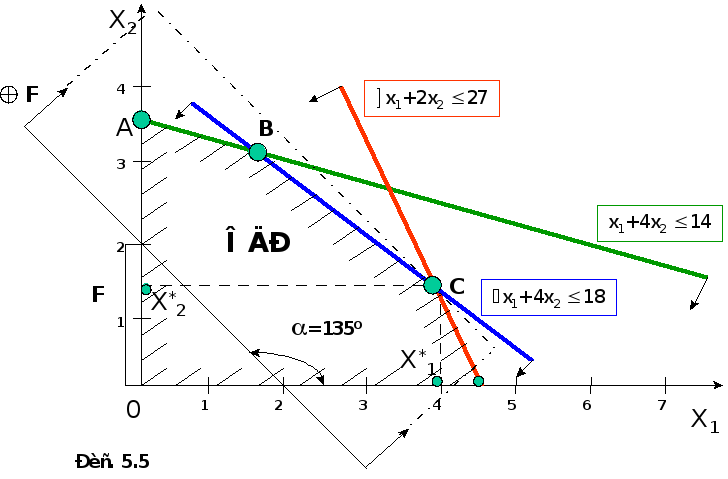
Составим математическую модель задачи.

x₁+4x₂  14

x₁+4x₂  18

(5.11) x₁+2x₂  27

x₁  0, x₂ 

математическая модель представляет собой систему линейных неравенств. Значит ОДР нашей задачи выпуклый многоугольник. Для удобства построения неравенства можно записать в форме, аналогичной уравнениям в отрезках:

x₁/14+x₂/7/2  1

x₁/6+x₂/9/2  1

(5.12) x₁/9/2+x₂/27/2 1

x₁  0, x₂ 

Если мы хотим найти оптимальное решение, то должны принять целевую функцию. Допустим, мы хотим, чтобы решение было оптимальным в смысле максимизации суммарного выпуска. Тогда целевая функция:

F=x₁+x₂  max (5.13)

Эту зависимость представим в виде x₂= F-x₁. Из графика данного уравнения (Рис. 5.1) следует, что tg= 1, при этом  =135^о, а величина F равна отрезку, отсекаемому прямой функции цели на оси координат. Если прямую перемещать параллельно самой себе в направлении, указанном стрелками, то эта величина будет возрастать. Очевидно, что оптимальным решением будут координаты точки С (x^₁; x^₂). При этом F=F^.

На основании рассмотренного, можно сделать исключительно важный вывод: оптимальным решением являются координаты вершин ОДР. А из этого вывода следует метод решения задачи линейного программирования.