5. Методы решения задач линейного программирования

5.1. Общая и основная задачи линейного программирования

К математическим задачам линейного программирования приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов (задача о раскрое, смесях и т.д.).

Во всех этих задачах требуется найти максимум или минимум линейной функции при условии, что ее переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этиx задач является частным случаем общей задачи линейного программирования.

 Oбщей задачей линейного программирования называется задача, которая coстоит в определении максимального (минимального) значения функции:

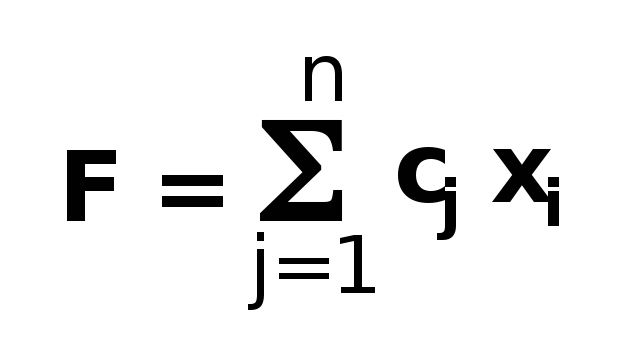(5.1)

при условии:

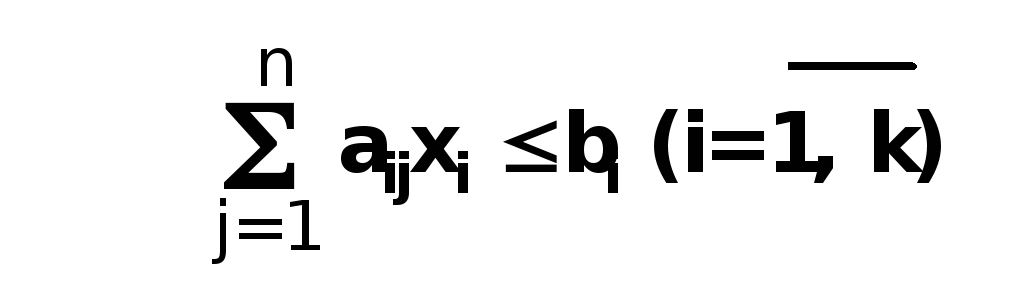(5.2)

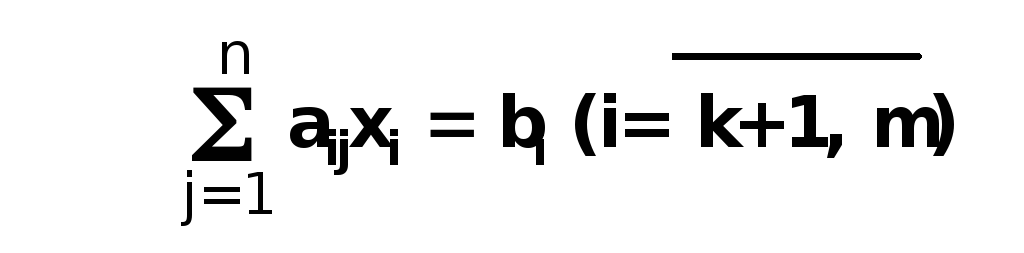(5.3)

X_j  0 (j=1, 1; 1  n) (5.4)

где a_ij, b_i, с_j - заданные постоянные величины и k  m.

 Функция (5.1) называется целевой функцией (или линейной формой) задачи (5.1)-(5.4), а условия (5.2)-(5.4) - ограничениями данной задачи.

 Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.2) и (5.4), где k=m и 1=n.

 Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.3) и (5.4), где k=0 и 1=n.

 Совокупность чисел Х^ = (x₁, x₂, ..., x_n), удовлетворяющих ограничениям задачи (5.2)-(5.4), называется допустимым решением (или планом).

 План Х^ = (x₁, x₂, ..., x_n), при котором целевая функция задачи (5.1) принимает свое максимальное (минимальное) значение, называется оптимальным.

значение целевой функции (5.1) при плане X будем обозначать через F(X). Следовательно, Х^ - оптимальный план задачи, если для любого X выполняется неравенство F(X)  F(Х^) (соответственно F(X)  F(Х^)).

5.2. Геометрический метод решения задач линейного программирования

Перепишем основную задачу линейного программирования в векторной форме: найти максимум функции

F=CX (5.5)

при условиях:

x₁P₁+x₂P₂+ ... +x_nP_n = P₀ (5.6)

Х 0 (5.7)

где C = (с₁, с₂, ..., с_n), Х = (х₁, х₂, ..., х_n); СХ - скалярное произведение; Р₁, Р₂, ..., Р_n и Р₀ - m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи.

 План X = (х₁, х₂, ..., х_n) называется опорным планом основной задачи линейного программирования, если система векторов P_j, входящих в разложение (5.6) с положительными коэффициентами x_j, линейно независима.

Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т.е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных. Haйдем решение задачи, состоящей в определении максимального значения функции:

F=c₁x₁ + с₂х₂ (5.8)

при условиях:

a_i1x₁+a_i2x₂  b_i (i=1, k) (5.9)

x_j  0 (i=1,2) (5.10)

Каждое из неравенств (5.9), (5.10) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми a_i1+a_i2=b_i (i=1, k), x₁=0 и x₂=0. В этом случае, если система неравенств (5.9), (5.10) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям.

 Так как множество точек пересечения данных полуплоскостей выпуклое, то областью допустимых решений (ОДР) задачи (5.8)-(5.10) является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

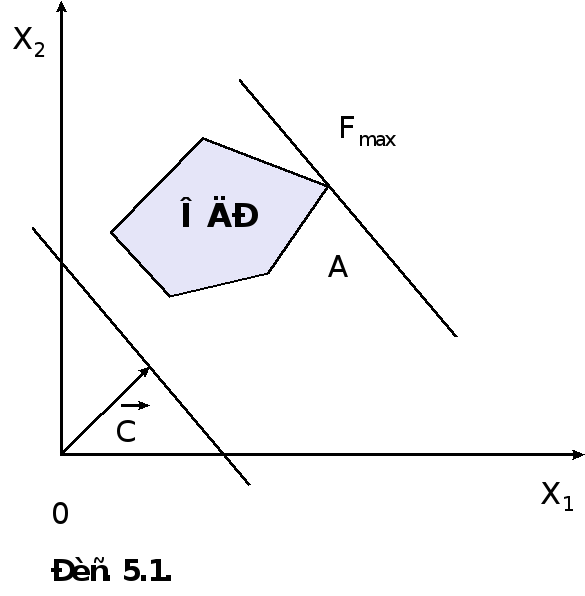
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки области допустимых решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин ОДР целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня c₁x₁+c₂x₂=h (где h - некоторая постоянная), проходящую через ОДР, и будем ее передвигать в направлении вектора C=(с₁; с₂) до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником ОДР. Координаты указанной точки и определяю оптимальный план данной задачи.

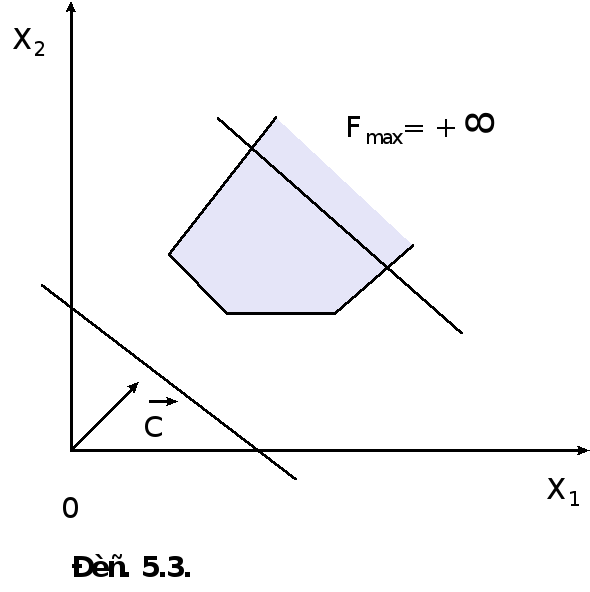
При нахождении решения задачи могут встретиться случаи, изображенные на рис. 5.1-5.4. Рис. 5.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рис. 5.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 5.3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 5.4 - случай, когда система ограничений задачи несовместна.

Oтметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тex же ограничениях лишь тем, что линия уровня c₁x₁+c₂x₂=h передвигается не в направлении вектора С, а в противоположном направлении.

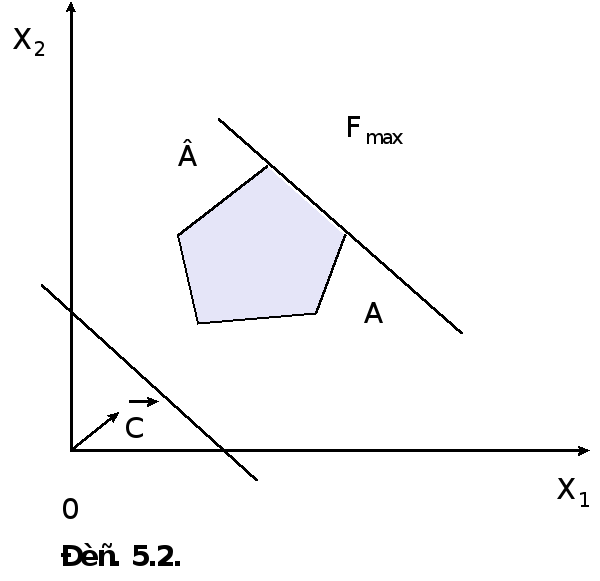
Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.