Симплексная таблица строится следующим образом:

В заглавной строке пишем последовательно векторы B, A₁, A₂, A₃, A₄ , A₅. Слева добавляем колонку «Базисные векторы», рядом с ней колонку «С», в которой поставлены коэффициенты при базисных переменных в линейной форме, в данном случае величины С₃, С₄, С₅. В последней строке, называемой индексной, и обозначаемой через  j-С_j, проставляются числа, равные значению линейной формы, в соответствием с уравнением (j=1, 2, 3, 4, 5). В итоге мы имеем таблицу 5.3.

Таблица 5.3.

Базисные	Коэффициенты	Вектор свободных	3	4	0	0	0
векторы	линейной формы С	членов В	A1	A2	A3	A4	A5
A3	0	56	4	9	1	0	0
A4	0	37	5	3	0	1	0
A5	0	2	-1	2	0	0	1
Индексная строка  j-Сj		0	-3	-4	0	0	0

Это первая симплексная таблица, соответствующая первому базисному решению: x₁=0; x₂=0; x₃=56; x₄=37; x₅=2. Значение линейной формы, равное нулю, мы записываем в первой клетке индексной строки.

Т.к. мы решаем задачу на максимум, то из выражения линейной формы видно, что имеет смысл увеличить x₁ или x₂. Действительно, коэффициенты при этих переменных в скобках отрицательны (а по существу положительны), и если мы положим x₁0 или x₂0, то значение  увеличится. Но эти же коэффициенты с их знаками стоят в индексной строке.

Итак, мы приходим к следующему выводу: наличие в индексной строке отрицательных чисел при решении задачи на максимум свидетельствует о том, что нами оптимальное решение не получено, и то, что от табл. 5.3 надо перейти к следующей.

Переход к новой таблице, т.е. к новой улучшенной программе осуществляем следующим способом: в индексной строке находим наибольшее по абсолютному значению отрицательное (а при задаче на минимум - наибольшее положительное) число. В нашем примере этим числом будет - 4. Найденное число определяет ведущий или ключевой столбец. Затем мы делим свободные члены на положительные элементы ведущего столбца и выбираем из полученных отношений наименьшее. Наименьшее отношение определяет ведущую строку. В данном случае имеем:

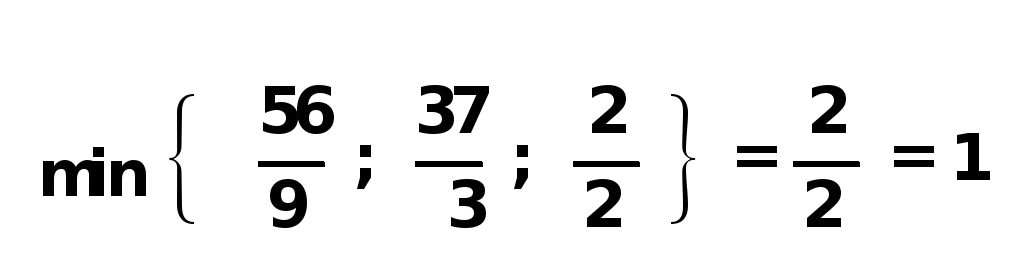
Таким образом, ведущей строкой будет строка A₅. На пересечении ведущего столбца и ведущей строки стоит разрешающий элемент. В нашем случае - это число 2.

Теперь мы приступаем к составлению второй таблицы или второго плана. Вместо единичного вектора A₅ мы в базис вводим вектор A₂. Переход к новому базису, как это известно, эквивалентен элементарному преобразованию матрицы, элементами которой служат числа табл. 5.3. А именно: в новой таблице элемент строки, соответствующий элементу ведущей строки прежней таблицы, равен этому элементу ведущей строки, разделенному на разрешающий элемент. чтобы получить любой другой элемент новой симплексной таблицы, нужно от соответствующего элемента прежней таблицы отнять произведение элемента ведущей строки на элемент ведущего столбца, разделенное на разрешающий элемент. Например, элементу 4 (табл. 5.3) будет соответствовать элемент табл. 5.4:

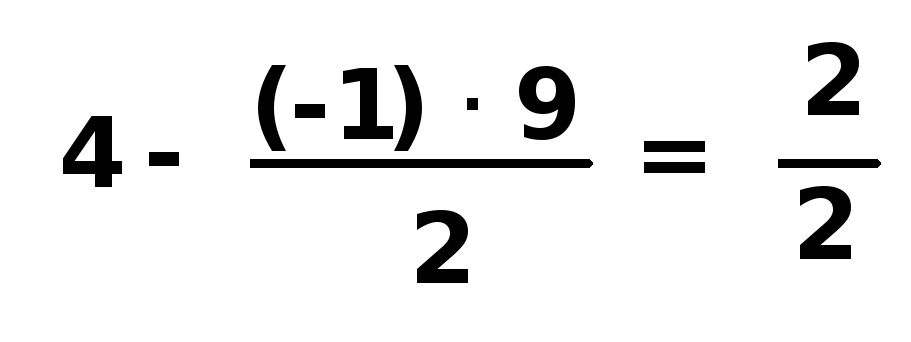
Таким образом, мы переходим ко второй таблице (таблица 5.4). Указанные выше преобразования относятся к столбцам B, A₁, A₂, A₃, A₄ , A₅.

Таблица 5.4.

Базисные	Коэффициенты	Вектор свободных	3	4	0	0	0
векторы	линейной формы С	членов В	A1	A2	A3	A4	A5
A3	0	47	17/2	0	1	0	-9/2
A4	0	34	13/2	0	0	1	-3/2
A5	4	1	-1/2	1	0	0	1/2
Индексная строка  j-Сj		4	-5	0	0	0	2

Из табл. 5.4 видно, что значение линейной формы возросло и теперь равно 4. Однако наличие в индексной строке отрицательных чисел свидетельствует о том, что это значение еще можно увеличить. Переходим к следующей симплексной таблице. число «5» определяет ведущий столбец. Находим ведущую строку. Для этого определяем:

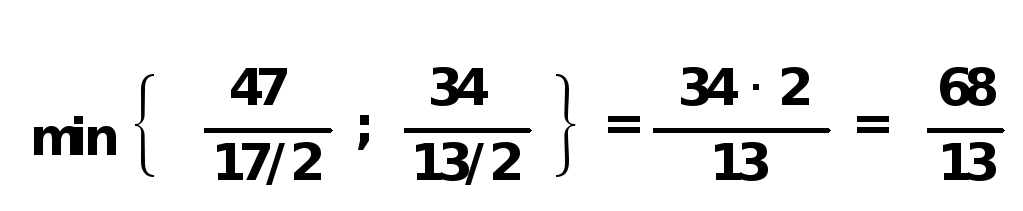
Итак, разрешающим элементом будет 13/2. Вектор A₄ выводим из базиса и вводим вместо него вектор A₁. Пересчет коэффициентов осуществляем по указанным выше правилам и получаем таблицу 5.5.

Таблица 5.5

Базисные	Коэффициенты	Вектор свободных	3	4	0	0	0
векторы	линейной формы С	членов В	A1	A2	A3	A4	A5
A3	0	33/13	0	0	1	-17/13	-33/13
A1	3	68/13	1	0	0	2/13	-3/13
A2	4	47/13	0	1	0	1/13	5/13
Индексная строка  j-Сj		392/13	0	0	0	10/13	11/13

В индексной строке нет отрицательных элементов. Следовательно, мы получим оптимальную программу. Оптимальное решение:

x₁=68/13; x₂=47/13; x₃=33/13; x₄ = x₅ = 0.