2.8. Метод вариации произвольных постоянных (метод Лагранжа)

Непосредственное нахождение частного решения линейного неоднородного дифференциального уравнения, кроме случая уравнения с постоянными коэффициентами, причём со специальными правыми частями, обычно представляет большие трудности. В связи с этим для нахождения общего решения ЛНДУ рассмотрим метод вариации произвольных постоянных, который всегда даёт возможность выразить общее решение ЛНДУ через элементарные функции и интегралы от них (в этом случае говорят, что решение «найдено в квадратурах»), если известна фундаментальная система решений соответствующего однородного уравнения.

Как было показано ранее, общее решение линейного однородного уравнения имеет вид:

, (8.1)

где – линейно независимые на некотором интервалерешения ЛОДУ, а– произвольные постоянные.

Будем искать частное решение ЛНДУ в форме (8.1), считая, что – не постоянные, а некоторые, пока неизвестные, функции отx:

. (8.2)

Продифференцируем равенство (8.2):

. (8.3)

Подберём функции итак, чтобы выполнялось равенство:. Тогда вместо (8.3) получим:

. (8.4)

Продифференцируем это выражение ещё раз по x. В результате приходим к:

. (8.5)

Подставим (8.2), (8.4), (8.5) в ЛНДУ 2-го порядка , после чего получим:

или

(8.6)

Так как – решения ЛОДУ, то равенство (8.6) принимает вид:

.

Таким образом, функция (8.2) будет решением ЛНДУ в том случае, если функции иудовлетворяют системе уравнений:

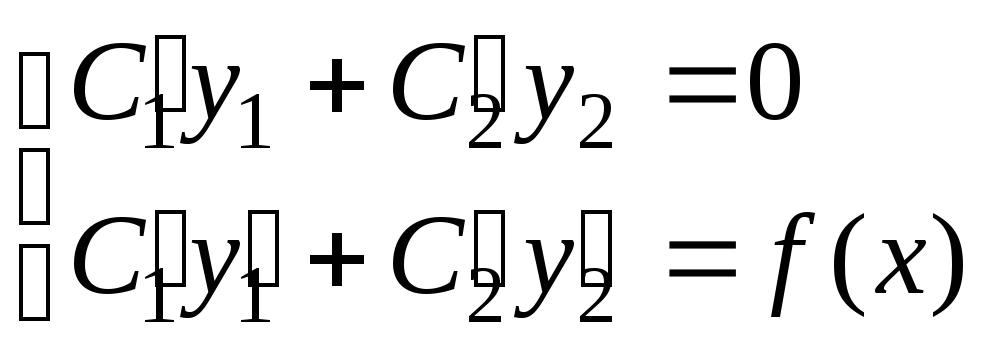(8.7)

Так как определителем этой системы является определитель Вронского для двух линейно независимых на интервале X решений соответствующего ЛОДУ, то он не обращается в нуль ни в одной точке интервала X. Следовательно, решая систему (8.7), найдем и:и. Интегрируя полученные равенства, заключаем:

, ,

где ,– произвольные постоянные.

Возвращаясь к равенству (8.2), получим общее решение неоднородного уравнения:

.

Пример. Решить уравнение: .

Решение. Соответствующее данному ЛНДУ однородное уравнение . Интегрируя его, получим общее решение:. Итак, двумя линейно независимыми решениями, образующими общее решение, являются функциии.

Предположим теперь, что общим решением заданного уравнения является выражение .

Для определения функций иимеем систему уравнений:

.

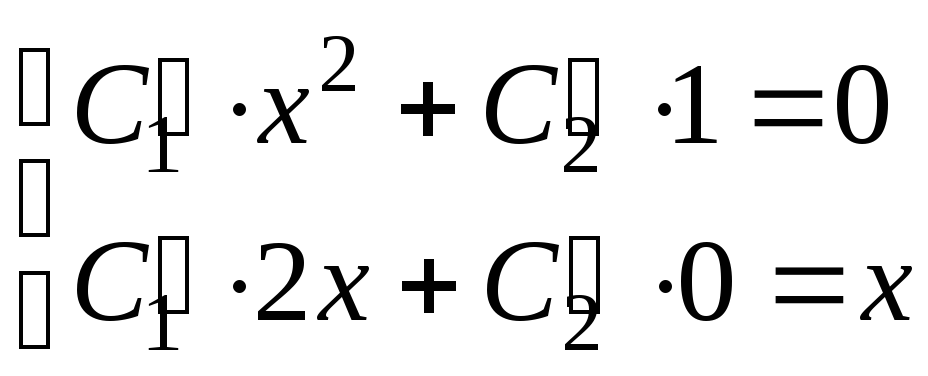Отсюда получаем ,.

Следовательно, общее решение заданного уравнения есть:

.

3. Линейные уравнения высших порядков

3.1. Однородное уравнение

Определение. Линейным уравнением n-го порядка называется уравнение вида:

. (1.1)

Если при всех рассматриваемых значениях x функция равна нулю, то это уравнение называетсяоднородным, в противном случае – неоднородным.

Предполагаем, что коэффициенты и свободный членопределены и непрерывны в интервале. Тогда уравнение (1.1) имеет единственное решение, определенное во всем интервалеи удовлетворяющее начальным условиям:, причём начальные данныеможно задавать произвольно, анужно брать из интервала.

Заметим, что линейное однородное дифференциальное уравнение (ЛОДУ) всегда имеет нулевое решение .

Для построения общего решения ЛОДУ достаточно знать n линейно независимых в интервале частных решений, то есть таких решений, для которых тождество

,

где – постоянные числа, может выполняться только при. Такая система решений называетсяфундаментальной. Известно, что для того чтобы система решений ЛОДУ была фундаментальной, необходимо и достаточно, чтобы её определитель Вронского

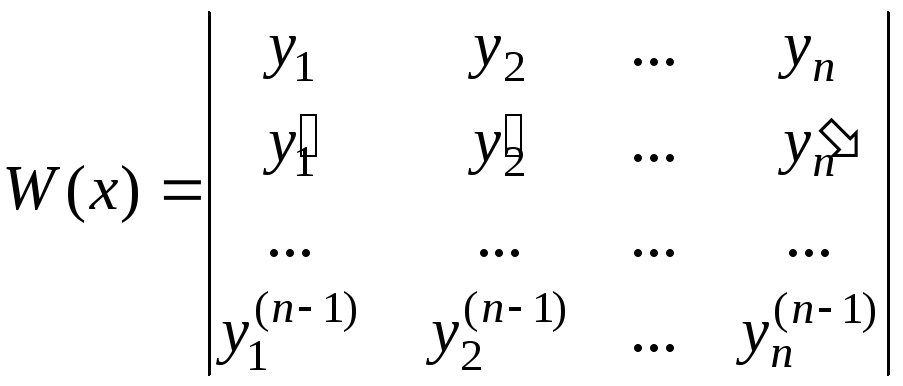
был отличен от нуля хотя бы в одной точке из интервала . В действительности, в этом случае определитель Вронского отличен от нуля во всех точках интервала .

Если найдена фундаментальная система решений ЛОДУ, то формула

, (1.2)

где – произвольные постоянные, даёт общее решение этого уравнения в области,,, …,.