1.2. Обыкновенные дифференциальные уравнения 1-го порядка

Обыкновенное дифференциальное уравнение 1-го порядка () имеет вид:или (если его удаётся разрешить относительно производной). Общее решение или общий интеграл уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядкапозволяет определить значение константы из общего решения или из общего интеграла. Таким образом можно найти частное решение, то есть задача Коши будет решена. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива следующая теорема, принимаемая здесь без доказательства.

Теорема. Если в уравнении функцияи её частная производнаянепрерывны в некоторой областиD плоскости XOY и в этой области задана точка , то существует (и притом единственное) решение, удовлетворяющее как уравнению, так и начальному условию.

Геометрически общее решение уравнения 1-го порядка представляет собой семейство кривых на плоскости XOY, не имеющих общих точек и отличающихся друг от друга одним параметром – значением константы C. Эти кривые называются интегральными кривыми для данного уравнения. Интегральные кривые уравнения обладают очевидным геометрическим свойством: в каждой точкетангенс угла наклона касательной к кривой равен значению правой части уравнения в этой точке:. Другими словами, уравнениезадаёт в плоскостиXOY поле направлений касательных к интегральным кривым.

Замечание: Необходимо отметить, что к уравнению приводится уравнениеи так называемое уравнение в симметрической форме.

1.3. Дифференциальные уравнения 1-го порядка с разделяющимися переменными

Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

(3.1)

или уравнение вида

(3.2)

Чтобы в уравнении (3.1) разделить переменные, то есть привести это уравнение к так называемому уравнению с разделёнными переменными, необходимо множители, содержащие переменную x перенести в одну сторону уравнения, а множители, содержащие переменную y, – в другую, а именно:

Остается проверить, не потеряны ли решения при делении на выражения, зависящие от переменных. Для этого необходимо решить уравнение . Если оно имеет вещественное решение ,то тоже будет решением уравнения (3.1).

Уравнение (3.2) приводится к уравнению с разделёнными переменными делением на произведение :

,

что позволяет получить общий интеграл уравнения (3.2):

(3.3)

Функции (3.3), определяющие интегральные кривые, будут дополнены решениями , если такие решения существуют.

Пример. Решить уравнение: .

Решение. Разделяем переменные:

; .

Интегрируя, получаем

.

Из уравнений инаходим,,. Непосредственной подстановкой этих функций в исходное уравнение убеждаемся, что эти решения – частные решения.

1.4. Однородные дифференциальные уравнения 1-го порядка

Определение 1. Уравнение 1-го порядка называетсяоднородным, если для его правой части при любых справедливо соотношение, называемоеусловием однородности функции двух переменных нулевого измерения.

Пример 1. Показать, что функция – однородная нулевого измерения.

Решение.

, ,

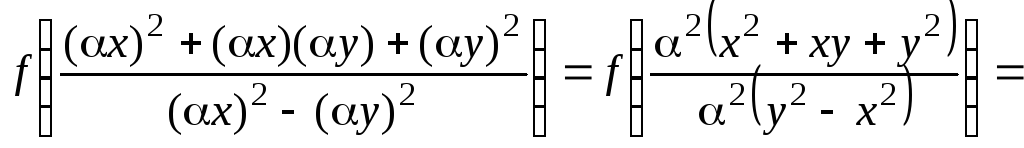
что и требовалось доказать.

Теорема. Любая функция – однородна и, наоборот, любая однородная функциянулевого измерения приводится к виду.

Доказательство. Первое утверждение теоремы очевидно, так как .

Докажем второе утверждение. Положим , тогда для однородной функции, что и требовалось доказать.

Определение 2. Уравнение

, (4.1)

где M и N – однородные функции одной и той же степени, то есть обладают свойством при всех, называетсяоднородным.

Очевидно, что уравнение (4.1) всегда может быть приведено к виду

(4.2),

хотя для его решения можно этого и не делать.

Однородное уравнение (4.1) приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле , где – новая искомая функция. Выполнив эту замену в уравнении (4.2), получим:

(4.3)

или

,

то есть

.

Интегрируя последнее равенство, получаем общий интеграл уравнения (4.3) относительно функции

,

который после повторной замены даёт общий интеграл исходного уравнения (4.2). Кроме того, если– корни уравнения, то функции(где) – решения однородного уравнения (4.2). Если же , то уравнение (4.2) принимает вид

и становится уравнением с разделяющимися переменными. Его решениями являются функции, определяющие на плоскости полупрямые:

.

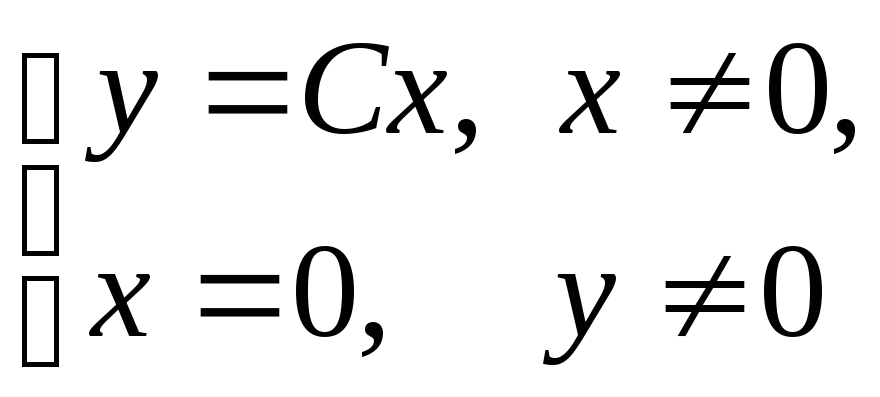Замечание. Иногда целесообразно вместо указанной выше подстановки использовать замену .