1.5. Дифференциальные уравнения, приводящиеся к однородным

Рассмотрим уравнение вида

. (5.1)

Если , то уравнение (5.1) с помощью подстановки, гдеи– новые переменные, аи– некоторые постоянные числа, определяемые из системы

,

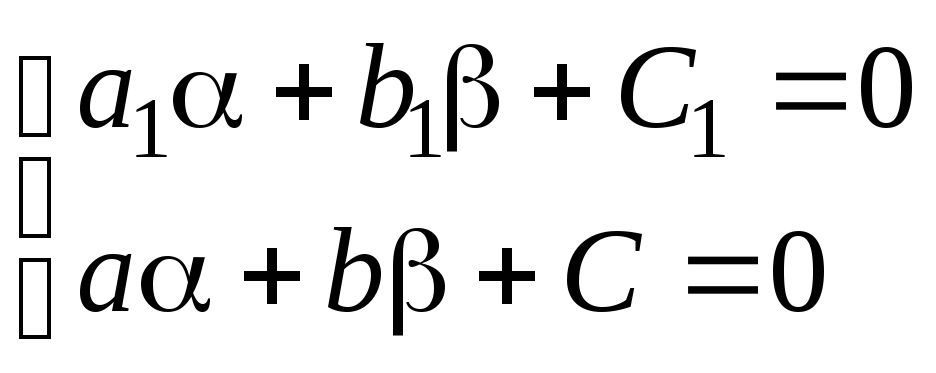приводится к однородному уравнению .

Если , то уравнение (5.1) принимает вид:

.

Сделав замену , получим уравнение, не содержащее независимую переменную.

Пример 1. Проинтегрировать уравнение

и выделить интегральную кривую, проходящую через точки:

а) (2; 2); б) .

Решение. Положим . Тогда

и

.

Сокращая на и собирая члены приdx и dz, получим

.

Разделим переменные: .

Интегрируя, получим

;

или

, где .

Заменяя z на , получим общий интеграл исходного уравнения в видеили, что то же самое,

. (5.2)

Равенство (5.2) определяет семейство окружностей

.

Центры указанных окружностей лежат на прямой и в начале координат касаются прямой. Функция , в свою очередь, является частным решением уравнения заданного дифференциального уравнения.

Определим, какие из найденных окружностей, удовлетворяют начальным условиям, то есть решим задачи Коши:

а) полагая в общем интеграле ,, находим , поэтому искомой кривой является окружность ;

б) ни одна из окружностей (5.2) не проходит через точку . Зато полупрямая проходит через указанную точку, а, значит ,соответствующая функция и даёт искомое решение.

Пример 2. Решить уравнение: .

Решение. Исходное уравнение является частным случаем уравнения (5.1).

Определитель в данном случае не равен нулю, поэтому сначала рассмотрим систему.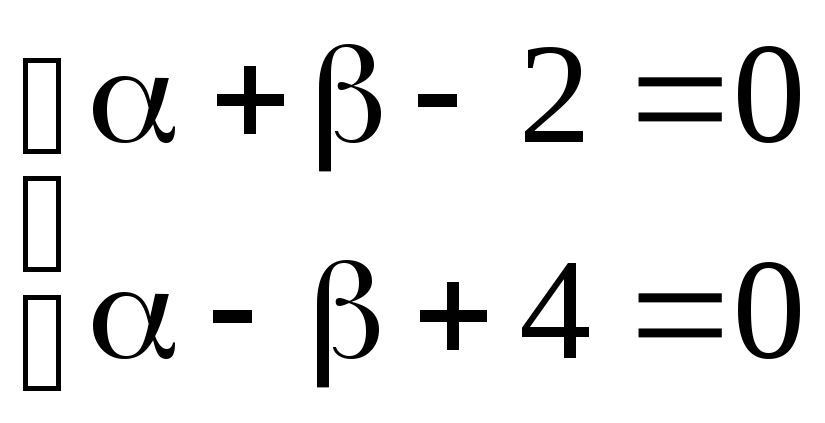

Решая указанную систему, получим, что . Выполняя в заданном уравнении замену, приходим к однородному уравнению

.

Интегрируя последнее уравнение после подстановки , находим. Возвращаясь к старым переменнымx и y по формулам , имеем.

1.6. Обобщенное однородное уравнение

Определение. Уравнение называетсяобобщённым однородным, если удаётся подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени m относительно x, y, dx и dy при условии, что x считается величиной первого измерения, y – k-го измерения, dx – нулевого измерения и dy – ()-го измерения.

Например, таковым будет уравнение

. (6.1)

Действительно, при сделанном предположении относительно измерений x, y, dx и dy члены левой части иdy будут иметь соответственно измерения (–2), (2k) и (k–1). Приравнивая эти величины, получаем условие, которому должно удовлетворять искомое число k:

.

Это условие выполняется при (при такомk все члены левой части рассматриваемого уравнения будут иметь измерение (–2)). Следовательно, уравнение (6.1) является обобщённым однородным.

Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки , гдеz – новая неизвестная функция. Проинтегрируем уравнение (6.1) описанным методом. Так как , то, а следовательно уравнение (6.1) примет вид:

.

Решая полученное уравнение путем разделения переменных, находим , откуда. Последнее равенство определяет общее решение уравнения (6.1).

1.7. Линейные дифференциальные уравнения 1-го порядка

Определение. Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и её производной. Оно имеет вид:

, (7.1)

где и – заданные непрерывные функции от x. Если функция , то уравнение (7.1) имеет вид:

(7.2)

и называется линейным однородным уравнением, в противном случае (≢0) оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

;

;

(7.3)

Выражение (7.3) определяет общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция обозначает ту же функцию, что и в уравнении (7.2), воспользуемся так называемымметодом вариации произвольной постоянной, который состоит в следующем: постараемся подобрать функцию так, чтобы общее решение линейного однородного уравнения (7.2) являлось решением неоднородного линейного уравнения (7.1). Тогда производная функции (7.3) примет вид:

.

Подставляя найденную производную в уравнение (7.1), получим:

или

.

Отсюда , где– произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет иметь вид:

. (7.4)

Заметим, что первое слагаемое в выражении (7.4) представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое – частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при . Сформулируем замеченный факт в виде теоремы.

Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения , то все остальные решения имеют вид, где– общее решение соответствующего линейного однородного дифференциального уравнения.

Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде . Тогда. Подставим найденную производную в исходное уравнение (7.1), получим:

.

Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) как общий множитель за скобку:

. (7.5)

Потребуем обращения в нуль круглой скобки: . Решим это уравнение, полагая произвольную постояннуюC равной нулю:

, .

Найденную функцию v(x) подставим в уравнение (7.5), откуда получим:

.

Решая его, приходим к: .

Следовательно, общее решение уравнения (7.1) имеет вид:

.